
ここには、線形代数に関する講義資料、補遺、余談などを置いておきます。 なお、講義に関する主たる情報は、大学の Moodle のページを参照してください。
「数学についての雑多な書き物のページ」
から、線形代数に関係する話をこちらに移動しました。
(2024-04-26)
例年 (昨年度までは基礎数理 I) 行列の要素の位置の数え方のときに している余談をあげておきます (今年は講義中にはしない予定なので)。
行列の要素は、左上を起点として、 上から i 番目、左から j 番目の位置にある成分を (i,j) 成分という風に数えます。これは通常の xy-平面の座標の見方とも 違いますのでやや戸惑いがあるかも知れません。 このような数え方は自然なのでしょうか。
同じ平面上の位置の指定の仕方として、将棋盤、碁盤の指定の仕方がありま す。将棋、囲碁とも平面を格子状に区切り、 そこに駒、碁石を乗せて並べていくわけですが、 将棋は格子で作られる長方形 (マス目) の中に、 囲碁は格子線同士の交点に並べるところが違います。
そして、もちろんマス目の数も違うのですが、 新聞の棋譜を見ると、棋譜でのそれぞれの位置の数え方も違うようです。
将棋は右上が起点、囲碁は左上が起点となっていて、 例えば将棋なら左上角に金があれば「9一金」と記録しますし、 囲碁なら右上角に黒石があれば「黒 19 の一」と記録するようです。
なお、上下を入れ替えると、 将棋の方は丁度 xy 平面の第 1 象限での座標の付け方と同じになりますが、 囲碁の方は xy 平面の x 軸を反対向きに取った座標の付け方 (つまり第 2 象限での座標の付け方) になります。
行列の要素の数え方は、囲碁の座標の付け方に似ていますが、 行列は縦の座標を先に数えるので、数える順番が違います。
他にも、例えば碁盤のように綺麗に配置されている町の区画の数え方があります。 札幌や京都が有名ですが、実はこれらも囲碁と将棋のような違いがあります。
札幌は計画都市として有名で、約 100m 四方の区画に綺麗に分かれています。 東西には南北に走る創成川通りを東西の起点 (y 軸) として 東何丁目、西何丁目という番号を振っていて、 南北には東西に延びる大通公園 (雪祭りの会場で有名) を南北の起点 (x 軸) として北何条、南何条という番号を振っています。 ただし、大通公園のすぐ北は「大通」で、その北から北一条、北二条、 のようになっています。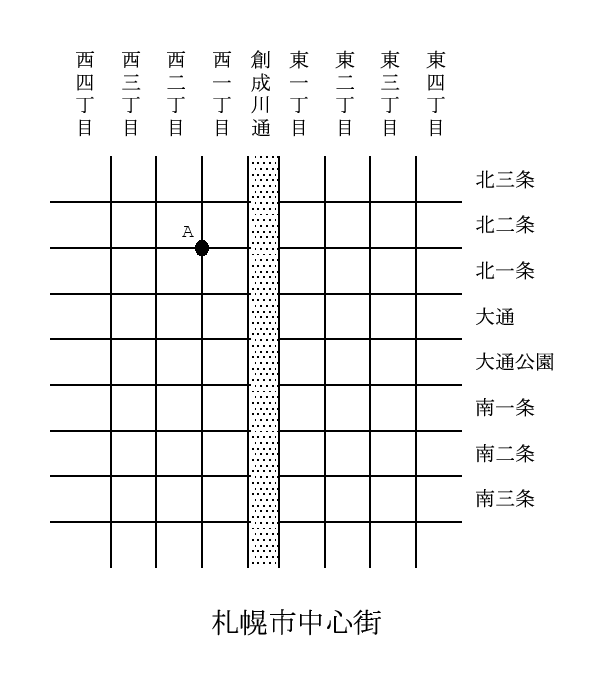
交差点の信号機には、その 2 つの角に丁名表示板がついていて 例えば図中 A の交差点には左上の区画の信号機に「北 2 西 2」、 右下の区画の信号機に「北 1 西 1」のように書かれていて、 それを見ることで現在の位置と方角がわかるようになっています (慣れないとちょっと考えますが)。
また、京都は昔の平安京が長安を真似て作った碁盤状の町で、 現在はかなりずれている部分もありますが、基本的に格子状の道路が 東西南北に走っています。
札幌は区画に名前がついていますが、京都は道路に名前がついています。 道路間の距離は札幌のようにきちんとはしていませんが、 やはり交差点にはどの通りとどの通りの交差点であるか (例えば「寺町二条通り」のように) 書かれていますので、 通りの名前と順番を覚えておくとだいたいどの辺りかが分かることになります。
その通りの覚え方には覚え歌のようなものがあり、南北の方は
まる (丸太町) たけ (竹屋町) えびす (夷川) に (二条) おし (押小路) おいけ (御池)東西の方は
あね (姉小路) さん (三条) ろっかく (六角) たこ (蛸薬師) にしき (錦小路)
....
てら (寺町) ごこ (御幸町) ふや (麸屋町) とみ (富小路) やな (柳馬場) さか (堺町) たか (高倉)のような文句 (わらべ歌) で覚えているそうです。
....
京都では住所にもこの通り名が使われていて、例えば京都市役所の住所は 「京都市中京区寺町通御池上ル」 となっています。 最後の「上ル」は寺町通りと御池通りの交差点を 北へ少しだけ行くことを意味します (同様に「下ル」「東入ル」「西入ル」という言葉が使われています)。
ただし、実際には京都にも区画に名前がついた町名はあるそうです。 例えば京都市役所は「上本能寺前町 488 番地」のようになるそうです。 しかし、例えば手紙の住所などは通常通り名の方だけが使われています。
札幌はマスに名前がつくので将棋盤方式、 京都は通りに名前がつくので囲碁方式と言えるでしょう。
なんとなく札幌方式の方がすっきりしているような気がして、 そちらの方がいいのかなと思ったのですが、 札幌出身で、どちらかといえば京都方式の方がいい、 と言われた方がおられました。 その方の話では、
札幌では住所 (例えば北一条東二丁目) を元に探し歩くと、 1 辺 100m の区画全部が同じ町名なので、 最悪の場合一区画を一周 (約 400m) しないと見つからないことがあるが、 京都なら交差点から出発して、どちらに進むかが東入ルなどのように 指示されているので、少なくとも次の通りまでの間に見つかり、 最悪でも通りと通りの間の距離しか探さなくてすむということでした。 皆さんはどう思われますか。
ふと気がついたのですが、 以下の本にまさに上記の将棋と囲碁、札幌と京都の例が載っています。
上に書いたことよりももちろん岩堀先生の本の方が古いですし、
私は昔この本をざっと読んだことがありますので、
その記憶があって上のことを書いたのかもしれません。
内容は一応岩堀先生の話よりも追加されていますが、
そういう意味では私のオリジナルとは言えない点がありますので、
上の内容のオリジナリティに関しては
「岩堀先生の本を読んで感じたこと」という程度に思ってください。
(04/13 2008)
3 次の行列式の計算はサラス-関のわかりやすい計算方法がありますが、 それは 4 次の行列式には使えません。
しかし、関は「解伏題之法」としてその方法を図にして説明しているようです。 私も以前どこかで見たような気がするのですが忘れてしまいました。 確か何枚かの計算方法により求めるというものだったと思います。
普通に考えると 4 次の行列式は 24 項の項が現われ、+ の物が 12 項、 - の物が 12 項あり、「サラス」式に + と - を重ねて図式化すると 1 枚で + が 4 項、- が 4 項の計 8 項書けることになりますから そのようなもの 3 枚で済むのですが、重ねなければ 6 枚です。 例えば以下のようになります。
これは単に左右に隣り合うものを線で結んでいるだけですが、 3 次の場合のサラスの方法はこれを外に回り込む線を使って 綺麗な覚えやすい対称性を持つ図式にしているわけです。 さて、この 4 次の場合の 6 枚の場合、うまく外に線を回り込ませて 覚えやすい形にできるでしょうか。 もし綺麗なものを思いついたら教えてください。 よさそうなものなら基礎数理でも使わせてもらうかも知れません。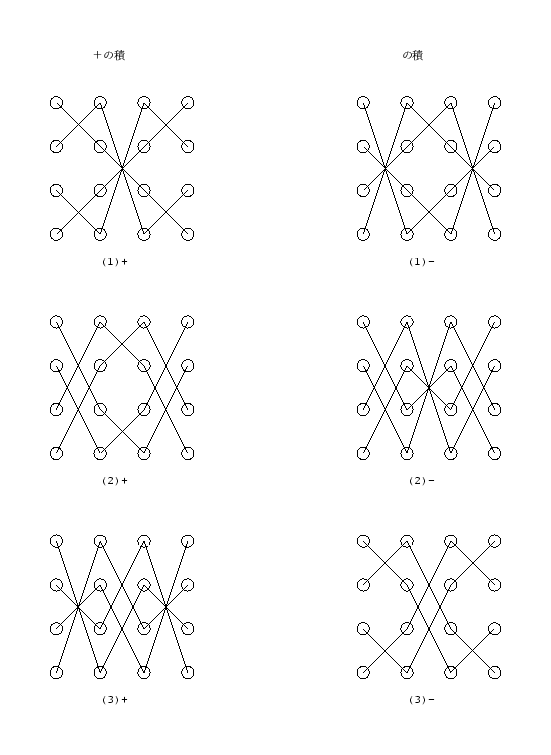
なお、+ と - を重ねて図式化して 3 枚にすると例えば次のように なります (青が +, 赤が -)。
う〜ん、何が何だか分かりませんね。
以前ここに置いていた図 (4 次の行列式の 6 枚の図式化, 4 次の行列式の 3 枚の図式化) は、良く見たら間違えていました。どうもすみませんでした。 また、一つサラスの方法に近い計算法も思いつきましたので以下で説明します。
それから上と同じサラス風の計算をするとさらに 8 つの項が出来ます。
追加情報ですが、
下の 「サラス−関の方法の拡張」 に、
これに関する理屈と、5 次以上の場合の拡張についての考察がありますので、
ご覧ください。
(07/26 2008)
線形代数の教科書では、行列式は順列の符号を使って定義されていますが、 講義ではその定義を採用せずに、 「1 列目での展開」によって帰納的な定義で説明しています。 ただ、このやり方だと、 その後の行列式の性質の証明が教科書通りにはいかなくなりますし、 中にはかなり難しくなってしまうものもあります。
講義ではそれらの証明はほとんど省いていますが、 帰納的な定義の場合のそれらの性質の証明を少し考えてみましたので、 ここにまとめておきます。
ただし、これらはかなり議論は煩雑ですし、 学生にとってはあまりおもしろいものではなく、 むしろ我々数学者等にしか興味のない話ではないかと思います。
HTML 版に PDF ファイルへのリンクを追加しました。
(01/12 2009)
2 次、3 次の行列式には、いわゆる「サラス−関」の計算法、 すなわち斜めに成分をかけるという計算方法がありますが、 4 次以上の行列には一般にそのような計算方法は「ない」とされていて、 ある行や列に関して展開する、あるいはその前に基本変形を行う、 といった方法が普通です。
しかし、4 次に関しては、 上の 「4 次の行列式」 で、 行の入れかえを行った 3 枚の配置を考えることにより、 サラス--関の方法に準ずる計算が行えることを紹介しています。
では 5 次以上の場合はどうかというと、 この場合はこれと同等の方法では項の数や積の計算がかなり多くなるので、 むしろ基本変形を利用する方がずっと楽なのですが、 原理的には同じ手法で 5 次以上の行列式の計算もできますので、 それに関する理屈も含めてまとめたものを以下に置きます。
HTML 版に PDF ファイルへのリンクを追加しました。
(01/12 2009)
連立一次方程式で、方程式の本数の方が未知数の数より多い場合、 線形代数の理論では、不要な方程式を捨て去ることによって解があるか ないかを論じますが、工学では最小自乗法を用いて、できるだけ すべての方程式を満足するような解を求めるのだそうです。 その証明を少しまとめてみました。
HTML 版に PDF ファイルへのリンクを追加しました。
(01/13 2009)
一次変換に平行移動を加えた変換をアフィン変換といいますが、 その変換が未知である場合、一般には未知数は 3*3+3 = 12 個ありますので、 それを点とその変換による移動から求める場合、12 本の連立方程式が必要です。 一点につき 3 本の連立方程式が得られるので 結局 4 点 (とその移動先の点) の座標がないと求められないのですが、 それが、回転 + 平行移動からなる合同アフィン変換の場合は、 3 点の移動だけで求められる、という話を機械系の方から聞きました。
しかもそこに (少なくとも私には) 面白いと思われる手法が使われていたので、 それを少しまとめてみました。
HTML 版に PDF ファイルへのリンクを追加しました。
(01/13 2009)
ある学生から、
「ベクトルの外積 a×b の大きさが、 その 2 つのベクトルが作る平行四辺形の面積となるのがわからない」という質問を受けました。 教科書では、それは定義なので、わからないと言われても困るのですが、 考えてみればベクトルの外積の具体的な計算問題では、 定義通りではなく通常は成分計算をやるので、 その大きさが定義通りに平行四辺形の面積になることは確かに自明ではなく、 教科書にもそれは書いてありません。
よって、ベクトルの外積の成分の式から、 ベクトルの外積の図形的な定義を導きだす、 ということを考えてみましたので、ここに置きます。
大学教養科目の線形代数では、行列、ベクトル、行列式などの一般論、 特に n 次元空間に関する一般論を教えますが、 逆に物理や工学などではより重要な 3 次元の 1 次変換の各論、 例えば回転変換などは普通は教えず、 「直交行列で行列式が 1 のものは回転を意味する」という話も、 それに触れることがあるかないか位だろうと思います。
私自身もちゃんと把握はしていなかったので、 あらためて直交行列と回転変換について少し考察してみたことを ここにまとめておきます。
行列 A, B の積 AB は、A の列ベクトルと B の行ベクトルの内積のような計算を そのすべての組に対して行って積 AB の成分をひとつひとつ求めていくのが その定義ですが、 実は列ベクトルや行ベクトルを使えば、いくつか簡単な表記、 便利な表記も成り立つことが知られています。
それらは、良く知られていることではあるけれども (初学者は誤解することがあるのでむしろ知らない方がいいかもしれないけれども)、 教科書には記されていないことが多いので、 それをここにまとめておきます。
数学では、要素が実数、または複素数である n 次正方行列 A に対する eA すなわち e の行列乗というものが考えられています。
行列乗は微分方程式への応用もあり、 厚めの線形代数の本には書いてある場合もありますが、 どの本にも書いてあるという内容ではないので、ここにまとめておきます。
また、行列乗の具体的な計算には、 通常ジョルダン標準形と呼ばれる行列変形を用いますが、 これも線形代数の入門的な本では扱っていないことも多いので、 これについても簡単に紹介します。
n 次正方行列 A,B に対し、 一般には AB=BA とはならず、 逆に AB=BA が成り立つとき A と B は可換であるといいます。
Ak と A とは、 AAk=AkA=Ak+1 より A と Ak は可換なので、 一般に多項式 x の多項式 f(x)=a0 + a1x + ... + amxm に対して B=f(A)=a0E + aA + ... + amAm と A は可換になります。
本稿では、この逆が成り立つか、 すなわち B が A と可換ならば、 なんらかの多項式 f(x) によって B=f(A) の形に書けるだろうか、 について考えてみます。
行列の逆行列は、余因子行列を行列式で割ったものになりますが、 定義通りに元の行列にかけて単位行列になるもの、 という計算をやると、そこにはベクトルの内積の計算が出てきて、 しかも、それが 0 となることからベクトルの垂直や、 特に 3 次の場合にはベクトルの外積の話がでてきます。
それを考えると、 余因子行列は元の行列の列ベクトルの外積で表されることになるのですが、 それをまとめたものを、ここに置きます。
補足ですが、上の資料の 4 ページ目に、計算例の式があり、 4 行目に行列式 |A| の計算結果が書かれています。 |A| は、3 次の行列のサラスの方法でも求められるのですが、 その前にベクトルの外積を求めてあるので、例えば
\(|A| = (\mathbf{a}\times\mathbf{b},\mathbf{c})\) = 6+6-2 = 10のようにして求めることができ、サラスの方法は必要ありません。
「線形代数」の講義で使用している教科書では、 幾何ベクトルを次のように定義しています (「定義 A」とする)。
いくつかの線形代数やベクトルに関する本を見ると、 このような方法、すなわち「ベクトル」=「有向線分」とする他に、 次のように定義するものもあります。
これらは、いずれも厳密な数学的な定義の議論というよりは、 「ベクトル」をどう認識するのが自然か、 どう説明するのが一番わかりやすいか、という立場の違いだろうと思います。 定義 D は、やや抽象的だが、幾何ベクトル以外のものにベクトルを広げる場合には、 あらかじめぼやかしておいた方が都合がいいこともあります。
個人的には、「有向線分 PQ」にははっきりと位置の情報が入っているので、 「有向線分 PQ」と「ベクトル \(\vec{PQ}\)」を分けて考える 定義 B, 定義 C の方が定義 A より分かりやすいと思いますし、 またベクトルの定義の中にベクトルの相等の話が入っていることで ベクトルの実体が厳密に限定できるようになるので、 本来は、教科書の定義 A よりも、 定義 C か定義 D のやり方が一番良いと思いますが、 本により定義がかなり違うということは、 皆がそう思っているわけではないのでしょう。
なお、物理や工学では、位置を無視したベクトル (通常のベクトル)
を「自由ベクトル」、
位置を「無視しない」ベクトルを「束縛ベクトル」のように呼んで、
位置を無視しないベクトルを考えることもあります。
これは、例えば物体を押す力などで用いられ、
どこを押すかでその物体への作用が変わってしまうので、
力の位置を固定して考えるときに用いたりします。
(09/28 2023)
教科書にも書いてありますが、工学など 3 次元のベクトルのみを扱う本 (ベクトル解析など) では、基本ベクトル (軸方向の単位ベクトル) を i,j,k のように書く場合があります。 この i は実は複素数の虚数単位 \(i=\sqrt{-1}\) に由来しています。
3 次元のベクトルという学問は、アイルランドのハミルトン (1805-1865) という学者によって考え出された四元数というものが元になっています。 四元数とは複素数をさらに広げて、 \(z=a+bi+cj+dk\) のような数を考えたもので、 この i,j,k は四元数の虚数単位で、 \(i^2=j^2=k^2=-1,\ ij=k,jk=i,ki=j,ji=-k,kj=-i,ik=-j\) のような数です。 c=d=0 なら通常の複素数になるので、これは複素数を含んでいます。
この四元数の a を除いた部分を使えば、 3 次元の物理現象などを綺麗に表現できるとして、 最初は四元数で現在のベクトルのような計算 (和、差、スカラー倍、 内積、外積) が行われたのですが、 四元数のままでは多少煩雑だったこともあり、 その後ギブス (1839-1903 米), ヘビサイド (1850-1925 英) らが \(ai+bj+ck\) の形の式を新たに「ベクトル」というものだと考え、 内積、外積もそれに対する新たな演算として定義することで、 現在の「空間ベクトル」という学問ができました。
現在も基本ベクトルとして i,j,k が使われるのは、
その四元数の名残りなわけです。
(10/06 2023)
\(\displaystyle \boldsymbol{a}=\left[\begin{array}{c}a\\b\\c\end{array} \right]\) ... (1)に平行で, 点 \(\mathrm{P}_0(x_0,y_0,z_0)\) を通る直線の方程式は, 教科書 (4.4) にあるように
\(\displaystyle \frac{x-x_0}{a} = \frac{y-y_0}{b} = \frac{z-z_0}{c} \) ... (2)となります。ただし、これが成立するのは \(a,b,c\) がいずれも 0 ではない場合です。
例えば \(c\) が 0 で \(a,b\) が 0 でない場合は, ベクトル方程式より
\(x=x_0+at,\ y=y_0+bt,\ z=z_0+0\) ... (3)となるので, t を消去すると,
\(\displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b},\ z=z_0\) ... (4)となります。これが注意 1 に書いてある (4.4)' です。これは,
\(\displaystyle y=\frac{b}{a}(x-x_0)+y_0,\ z=z_0\) ... (5)と書き換えることも可能で, (4) の最初の式は xy 平面の直線の式と同じ形になります。
\(c=0\) という場合は, (1) の方向ベクトル \(\boldsymbol{a}\) の z 成分が 0 なので, \(\boldsymbol{a}\) は xy 平面に含まれるベクトルになります。 よって, それに平行な直線は xy 平面に平行な平面 \(z=z_0\) (高さ \(z_0\) で水平な平面) に含まれるので, 直線の方程式は上のような形, すなわち xy 平面の直線の式と \(z=z_0\) の組み合わせ, となるわけです。
なお, 厳密に言えば, \(z=z_0\) は xy 平面に平行 (z 軸に垂直) な平面の方程式で, もう一つの
\(\displaystyle \frac{x-x_0}{a}=\frac{y-y_0}{b}\) ... (6)は, 一見 xy 平面上の直線のようですが, z 座標はなんでもいいので, その xy 平面上の直線を真上に移動して描かれる軌跡としての「平面」 (z 軸に平行な平面) の方程式になっています。 元の直線は, その 2 つの平面の交線として現れます。
ついでにいえば, 一般の (2) の方程式も, = が 2 つあるので, これは (6) と
\(\displaystyle \frac{y-y_0}{b}=\frac{z-z_0}{c}\) ... (7)の 2 本の等式からできていて, (6) は xy 平面の直線を z 軸に沿って移動した軌跡の平面, (7) は yz 平面の直線を x 軸に沿って移動した軌跡の平面を表していて, (2) の直線はその交線として現れるものになっています。
さらに \(a\neq 0, b=c=0\) の場合は \(\boldsymbol{a}\) が x 軸に平行なベクトルになるので, 直線は \(\mathrm{P}_0(x_0,y_0,z_0)\) を通って x 軸に平行な直線となり, よってその方程式は
\(y=y_0,\ z=z_0\) ... (8)となります。これが教科書の (4.4)'' です。
(8) には一見 x の条件がありませんが, x は \(x=x_0+at\) よりなんでもよい,
すなわちすべての実数を取ることになります。
見方を変えれば, この (8) も, xz 平面に平行な平面 \(y=y_0\) と
xy 平面に平行な平面 \(z=z_0\) の交線と見ることができます。
(10/20 2023)
この講義で使用している線形代数の教科書には書かれていませんが、 N 次正方行列 A の N 乗 \(A^N\) は、 \(E, A, A^2,...,A^{N-1}\) の定数倍の和で表すことができる 「ケイリー・ハミルトンの公式」と呼ばれるものが知られています。
その公式の紹介と、その応用として行列の累乗の計算の簡略化について まとめてみましたのでここに置きます。 なお、行列の累乗の計算は、行列の応用としてはそれなりに意味があり、 その簡略化は有益だろうと思います。
2 次の行列の逆行列に関する定理は以下のようになります。
教科書はこの定理 (定理 11.1) の証明を、 連立方程式を解くことで証明していますがが、 ここでは、もう少し易しい別な証明を紹介します。
\(A^{-1}\) の前の分数を除いた部分の行列を \(\displaystyle \tilde{A}= \left[\begin{array}{cc}d & -b\\-c & a\end{array}\right] \) とすると、\(A\tilde{A}=\tilde{A}A = (ad-bc)E\) となることは、 実際に計算することで容易にわかります。これを利用します。
この式から、もし \(ad-bc\neq 0\) ならば \(\displaystyle X=\frac{1}{ad-bc}\tilde{A}\) が \(A^{-1}\) の定義を満たすこと、よって A が正則であることがわかりますので、 上の 2. と 1. の十分条件の方はこれで OK です。
あとは 1. の必要条件の方、すなわち「A が正則ならば \(ad-bc\neq 0\)」 となることを証明すればいいわけですが、 それには A が正則、すなわち \(A^{-1}\) があるのに、 \(ad-bc=0\) だとすると矛盾が起きることを示します (背理法)。
\(ad-bc=0\) の場合は \(A\tilde{A}=\tilde{A}A = (ad-bc)E=O\) となりますが、
\(A^{-1}\) が存在すれば、これをかけると
\(A^{-1}A\tilde{A} = E\tilde{A}=\tilde{A}=A^{-1}O=O\) となり、
\(\tilde{A}=O\) となります。
よって、その成分を比較することで、\(a=b=c=d=0\) であることがわかります。
これは、\(A=O\) を意味しますが、\(O\) には逆行列は存在しないので、
\(A^{-1}\) が存在することに矛盾します。
(証明終わり)
(11/30 2023)
講義で紹介した、3 次の行列式の計算法として名前を残している、 サラスと関について紹介します。詳しくは、以下をご覧ください。
まず、サラスはフランスの数学者 P.F.Sarrus (1798-1961) で、 実はあまり詳しいことは知られていません。 歴史上の数学者の一覧 (例えば MacTutor) などにもでていません。 上の論文には詳しく書かれていますが、 すぐれた業績を上げた数学者、というわけではないため、 それほど人物が広く知られてはいないのだろうと思います。
「サラスの方法」として線形代数の本には広く紹介されているのですが、 そこに名前が残ることからすると、 広く使われた線形代数の教科書のようなものを書いた人なのかと思っていましたが、 上の論文によればどうやらそうでもないようで、 むしろ「広く使われた線形代数の教科書」で 「サラスの方法」として紹介されたので、それで名前が残っている、 という話のようです。
次に関ですが、関孝和 (1642?-1708 群馬県藤岡市) という日本の数学者です。 当時の日本の数学を「和算」と呼びますが、 関流という和算のグループを作りました。 行列式については、西欧ではライプニッツが 2 次、3 次の行列式を 1693 年 に発見しているのですが、関はそれより早い 1683 年に 4 次、 5 次の行列式まで求めています (ただし 5 次は少し間違いがあったらしいです)。 ベルヌーイよりも早くベルヌーイ数を見つけているなど、 世界的な業績をあげている人なのですが、 当時は鎖国中で西欧との文化交流はほとんどなく、 よって関の数学を西欧の人が触れることはなく、 また、関流の数学はしばらく門外不出でもあったため、 関の数学についてはあまり評価されてきませんでした。 しかし最近では、その業績が認められ、MacTutor でも紹介されています。
そこに、「Takakazu Seki was a Japanese mathematician who was the
first person to study determinants.
He also discovered Bernoulli numbers before Jacob Bernoulli.」
のように書かれています。
西欧からの情報が入ってこない中で、
西欧に劣らない独創的な研究をしているところが驚異的で、
和算は日本が誇れる文化の一つでもあります。
(12/08 2023)
簡易的な、そして工学で良く使われている線形代数の教科書では、 固有値・固有ベクトルの応用としては行列の対角化以外には あまり紹介されていないものが多いように思います。
その応用例をいくつか紹介します。
対称行列、交代行列は直交行列、 およびユニタリ行列によって対角化できることが知られています。
さらに交代行列は実数成分の直交行列によって、 対角行列とは別の形の標準形に変形できることも知られていますが、 交代行列はあまりメジャーではないせいか、 標準形の結果はいくつかの線形代数の教科書などには見られるものの、 その変形の詳しい話があまり紹介されていません。
そこでそれをまとめてみましたので、ここに置きます。
上の「対称行列・交代行列の対角化」で、 エルミート行列、歪エルミート行列のユニタリ行列による対角化と、 対称行列と交代行列の直交行列による標準形への変形を紹介しました。
一方で、この対角化、標準形については、次のことも良く知られています。
これらは、いくつかの本や資料などで既に紹介されていますが、 「対称行列・交代行列の対角化」の続きとして ここにまとめておきます。