(07/15 2001)
講義中に配布した宿題の解答例などの配布プリントを、 画像ファイルと PDF ファイルにして置きます。 手書きなので多少 (かなり ?) 見にくいですが配布しているものと同じものです。
期末試験の採点をしていて、気になった誤答等がありました。 小テストに関しては講義中に指摘しましたが、 期末テストに関しては話す機会がありませんので、 ここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
基礎数理 II は、現在 (2009) は基礎数理 I の続きの微積分をやっているのですが、 基礎数理 I と II ではクラス分けが異なる (I は 3 クラス、II は 2 クラス) ため、 基礎数理 I の B クラスだった学生が基礎数理 II の B クラスに来ると 最初とまどう、という話を例年聞いていました。
授業が進むとあまり問題はないようなのですが、 今年 (2009) は試みとして、希望者に 3 回だけ演習形式で 基礎数理 I C クラスの内容の補習を行いました。 学生の参考になるかもしれませんので、その配布資料をここに置きます。
教科書に、定積分による置換積分、部分積分の公式がのっていますが、 講義中に注意したようにその運用にはミスが多いようです。よって、 置換積分、部分積分は定積分では行わず、不定積分でのみ使用して、 そこで求めた原始関数を利用して定積分の値を計算する、という方法を 講義では紹介しました。
その後、もう一つ別な工夫を思いつきました。この方法の方が、 その運用には誤解が少なくなるような気がします。 また、定積分と不定積分自身の違いもより明確になるのではないかと思いますので、 それをここに紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
リーマン和の極限で定積分を定義する区分求積法を講義中で紹介しましたが、 極限として面積になる、というところは実際には多少ごまかしがあります。 つまり、リーマン和はあくまで面積の近似でしかなく、その極限を取ると、 その誤差が 0 に収束するということを、本当は証明する必要があります。
連続関数のグラフに対しては、それが証明できるのですが、教科書には その証明は書いてありません (定理 12.2)。 それは、一般の連続関数に対してそれを証明するには、他にまだいくつかの 事柄 (例えば極限や連続性の厳密な定義、連続関数の一様連続性という性質など) が必要になるからです。
しかし、f(x) が微分可能で、f'(x) も連続であるような場合には多少簡単に (とはいっても十分面倒ですが) それを説明できますので、ここで紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
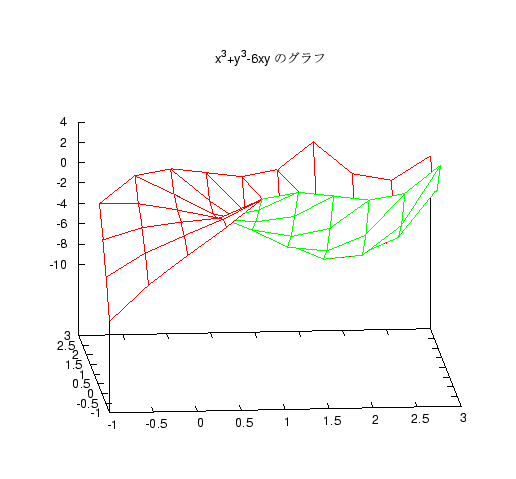
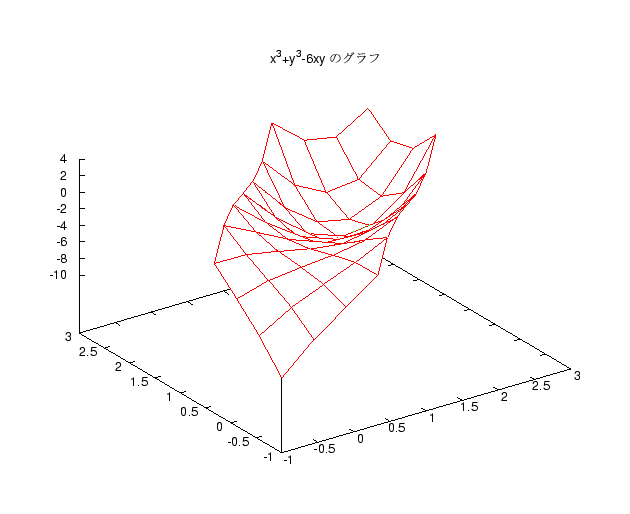
講義中に 2 変数関数の極大極小の問題として、z=x3+y3-6xy を取り上げ、 そのグラフも紹介しましたが、グラフは多分見えにくかっただろうと思います。 よって以下にそのグラフを置いておきますのでご覧ください。
(07/15 2001)
後期試験、木曜 5 限の方 (情報電子) では次のような立体の体積を求める問題を 出しました。
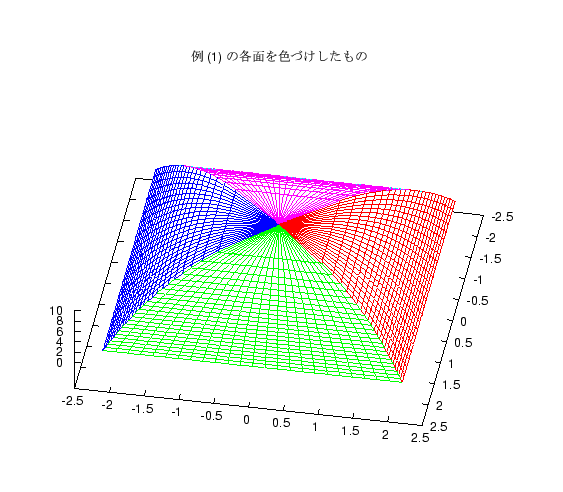
高さ 10 の立体があり、高さ x でのその立体の水平断面が、 一辺の長さが 2(10-x)^(1/3) の正方形であるとき、 この立体の体積を求めよ。 (^ は累乗だと思ってください)そのような立体は色々考えられますが、まず 2 つの例をグラフで紹介します。
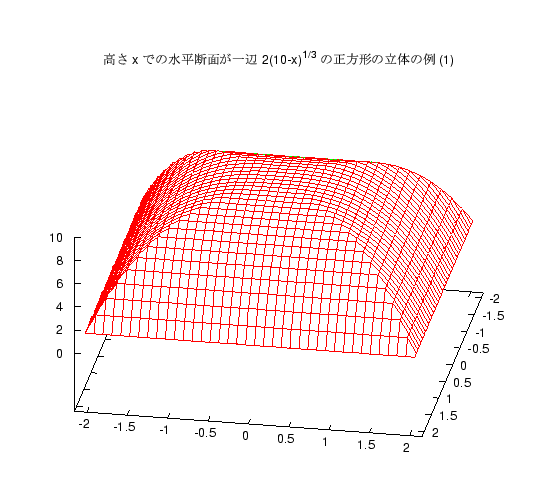
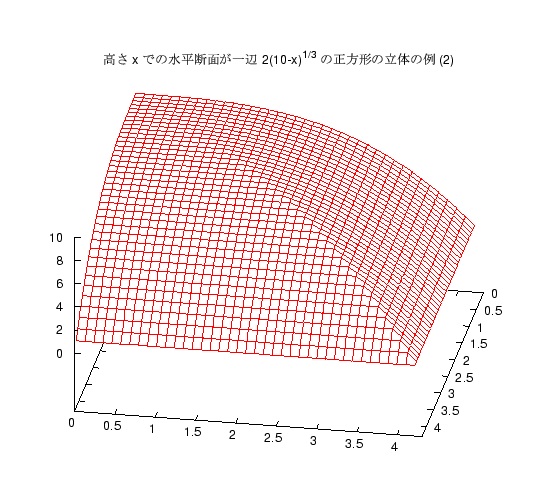
答案に図形を書いている人もいましたが、 残念ながらこれに似た形の立体はほとんどなく、 直方体、あるいはそれが多少ゆがんだものを書いている人が多かったようです。 頂上 (x=10) では明らかに断面積 0 なのですが、 それには気がついた人はわずかしかいませんでした。
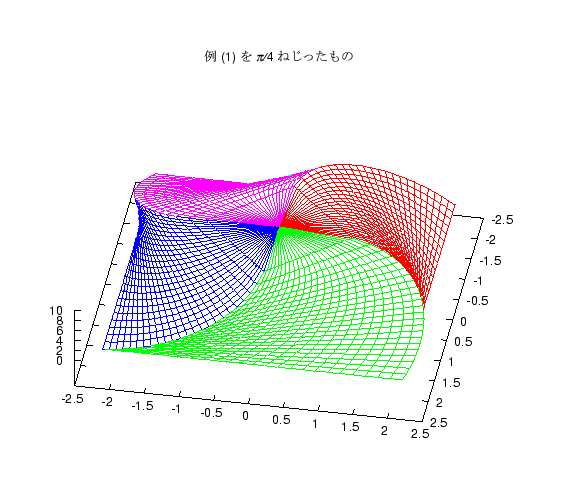
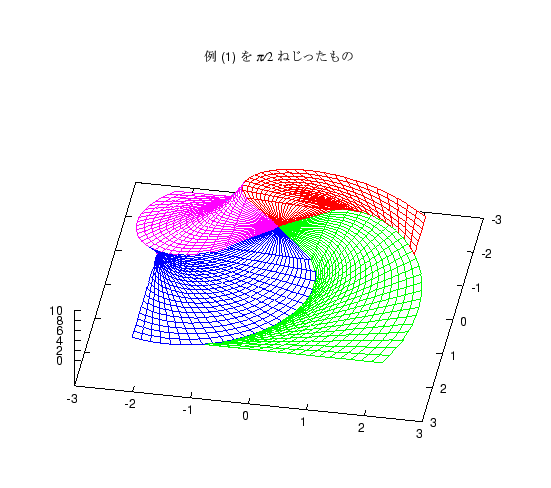
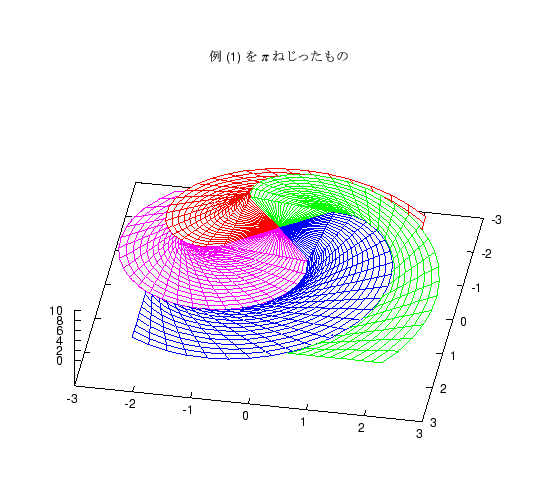
上の 2 つの立体は、各断面の正方形を中心に置くか、端に置くかの違いですが、 これをねじったものも題意を満たす立体になります。 これに気がついてねじった図を答案に書いた人もいましたが、 やってみるとわかりますが、 ねじる角度が大きいと途中の面が底面をはみ出る図形になります。 そのような図形を紹介します。
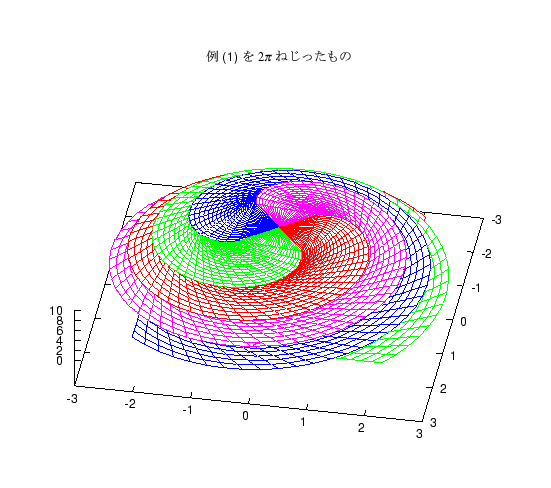
(07/29 2001)
毎年偏微分の合成関数の微分法の所になると、 教科書には載っていませんが x の x 乗の微分の例を紹介しています。 これは最初の年の学生から教えてもらった話を元にしたものです。
ついでにその極限である "0 の 0 乗" の話を追加して ここに紹介することにします。
なお、少し誤解を受けそうな箇所があったので、追記を加えました (03/05 2006)。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
毎年有理関数の積分に関して部分分数分解による方法を紹介していますが、 そこに出て来る一番難しい形のものの積分は 時間の都合上易しいもののみを説明をし、 一般的なものの説明は省略することが多いので、 一般的なものも含んだ説明をここで紹介しておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
これに加えて、実際の計算のしやすさを、もう少し考えてみました。 これも紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
教科書には書いてありませんが、 例年講義で紹介している「部分分数分解の原理」の証明も書いてみましたので これも紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
一番難しい形の有理関数に関しては、 複素数を利用した部分分数分解でやる、 という方針も立つのですが、実はそれはそんなに簡単ではありません。 これについても少しまとめてみましたのでここに紹介します。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
積分の定義のところで区分求積の話をしていますが、 これを利用すると、無限級数
1-1/2+1/3-1/4+1/5-1/6+...の値を求めることができます。 初等的な計算のみでできますので、 その計算をここで紹介します。
ただし、「区分求積」の例として適切なものだとはいえないでしょう。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
高次導関数に対する積の微分の公式として「ライプニッツの公式」と 呼ばれるものがあります。 これは、範囲としては基礎数理 I で履習する範囲のものですが、 偏微分を使う証明で、通常の証明 (帰納法) よりも よりこの公式の意味を説明するようなものを考えましたので、 ここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
直接基礎数理 III とは関係はありませんが、 数学には、色んな場面で「n 次元球 (2 次元の円、3 次元の球の拡張) の体積」 が出てきます。 それは、大学の多変数の積分の演習問題として扱われることが多いのですが、 対称性を利用して多少おおざっぱな考察をすれば 、 1 次元の定積分で計算できなくはありません。
それには、cosθの n 乗の定積分の計算 (部分積分) なども出てきて、 基礎数理 III の応用にもなると思いますので、 この計算を実際にやってみた例をここにまとめておきます。
PDF ファイルと、HTML 版にそれへのリンクを追加しました。
(01/12 2009)
以前、ある大学院生に次のような質問をされたことがあります。
マイコンに勾配 (タンジェント) の値からその角度を求める プログラムを載せようと思っているが、 アークタンジェントのマクローリン展開を 使うと誤差が大きくなってしまうのだがどうしたらよいか。元々マクローリン展開は x=0 での展開式なので |x| の値が大きい場合はその誤差が大きくなってしまいます。 しかしうまく工夫すれば、そのマクローリン展開でも ある程度の精度で計算できます。 それについてここにまとめておきます。
ジェットコースターのようにくねくねと変化する曲線上を質量のある物体をすべらすと、 その上に凸な部分で速度が出すぎるとその曲線を離れ得ます。
それが起こるための曲線と速度との関係を、 テイラー展開を用いて求める方法を思いついたので、 それをここにまとめておきます。
道路のカーブの曲がり具合を表すのに、R=200 のように表現することがありますが、 それは「円で言えばその半径が 200m くらいの曲がり具合である」という意味です。
一般の曲線に対しても、実際にはそれが円の一部ではなくても、 円で言えばそれがどれくらいの半径の曲がり具合であるか、 ということを表現する 曲率半径 と呼ばれるものがあります。 工学では出てくる場面は多少ありそうな気がしますが、 本学 1,2 年生の微積分の教科書には書かれていないようなので、 どのようにしてそれが得られるのかをここにまとめておきます。
cosmx・sinnx (m, n は 0 以上の整数) の不定積分の計算はよくある問題ですが、 基礎数理 II で使用している教科書には書いてなかったので、 今年度 (2009) の宿題の解答として配布した手書きのプリントの余白に、 余談としてその積分方法を何通りか紹介しました。
せっかくなので、省略した部分も加筆して、 ここにそれをまとめておきます。
部分積分の公式というと、大学向け、高校向けのどの教科書も、
公式 1: ∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dxの形で書いているものが多いのですが、 現在基礎数理で使用している教科書では、
公式 2: ∫f(x)g(x)dx = f(x)G(x) - ∫f'(x)G(x)dx (G'(x)=g(x))と書いてあります。これは公式 1 の u(x) を f(x)、 v(x) を G(x) と見た形になっています。
これらも含めて、その他の方法についても少し考察してみましたので、 ここにそれをまとめておきます。
双曲線関数は、三角関数と似た記号を使って書かれるものですが、 実際には指数関数の簡単な式で定義される関数なので、 特に新しい関数として追加されるようなものではなく、 よって数学の教科書でも定義とそのグラフ程度しか紹介されないことが多いようです。
実際、基礎数理の教科書でも、 定義と簡単な性質が発展として 1 頁書かれているだけです。
そこで、せっかくですから、 この関数の他の性質などを、余談も含め色々調べてみましたので、 ここにそれをまとめておきます。
