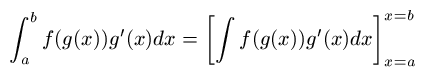
講義に関して出た質問と回答をここに上げておくことにします。 なお、ここの回答は原則竹野による回答です。
基礎数理 II と基礎数理 III の内容が、2007 年度後期から
(2007 年度入学生から) 入れかわっています。
よってここの QandA は、2006 年以前の入学生にとっては基礎数理 III、
2007 年度以降の入学生にとっては基礎数理 II の QandA になっています。
(01/27 2008)
1.
講義のやり方での定積分の置換積分は、
置換したところで範囲も変換してもよいか
2. 答案に書かれている○、□、△、×はどういう意味か
3. 答案に書かれている L の反対 (」) のような記号は、
こう書け、という意味か
4. \(f_x(x,x)\) はどういう意味か
5. 留年生、再履修者はこの基礎数理 II を取れるか
6. B クラスから A クラスに移りたいのですが
7. 部分分数分解で分母が 0 になる値を代入していいんですか
8. \(e^{700}\) の値が関数電卓で出ません
9. ある文字がわかりにくい
10. \(y^{(4)}\) は \(y''''\) と書いてもいいか
11. 極大値、極小値は「max」「min」
と書いてもいいか
12. 3 次関数の増減表の f' の符号は
係数から決めてもいいか
13. 商の微分で式がごちゃごちゃになるが良い方法は
14. 「問」に変な漢字を使う理由がわからない、見にくい
15. 合成関数の微分は高校で習ったやり方で解いてよいか
16. \((4+2x)e^x\) という解答は別の書き方でもよいか
目次に戻る
これは、講義で紹介した定積分の置換積分の話で、 私の紹介したやり方は、まず
のように、定積分を不定積分の値の差と書き直し、 その上で不定積分のレベルで置換積分を行い (u=g(x))、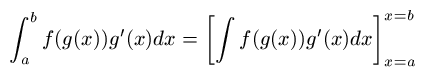
のように計算し、最後は、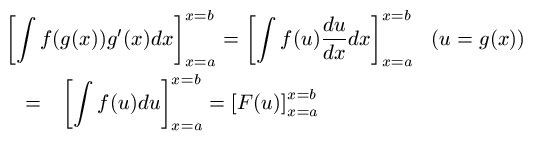
のように中の式を x に戻して x=b, x=a を代入して差を計算してもいいですし、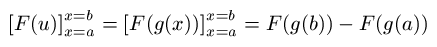
のように代入する方の値を u に直して u=g(b), u=g(a) を代入して差を計算してもいい、という話をしました。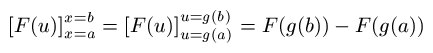
で、この質問は、最初の置換積分を行う段階で、外に出ている代入する値を
のように変換してしまっても構わないか、というものでした。 もちろん、これでも構いません。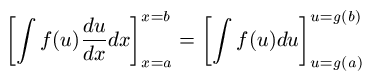
しかしそれができるようなら
それは本質的に定理 27.1 でやっているのと変わらないので
(私の方法を使うメリットも少し減る)、
無理矢理私の方法でやらなくても、
最初から定理 27.1 でやっても構いませんよ。
(06/13 2005)
○は正解、□はちょっと惜しい (少し減点)、△はもう少し悪い (もう少し減点)、 ×は不正解 (点数はあげられない) を意味しています。 それぞれの点数は問題によって違います。
なぜ□を△よりもいいものを表すのに使うのかというと、
□の方が△よりも○に近いからです。
(08/03 2005)
いや、違います。それは私の採点のときに書く記号で、
そこまでは合ってる、ということを意味します。
それを目安にすれば、どこで間違えているかわかるでしょう。
(08/03 2005)
これは、 「f(x,y) を x で偏微分した式 (\(=f_x(x,y)\)) に y=x を代入したもの」 になります。 同様に、\(f_y(x,x)\) は、 「f(x,y) を y で偏微分した式 (\(=f_y(x,y)\)) に y=x を代入したもの」 となります。limit を使って言えば、\(f_x(x,x)\) は、
\(\displaystyle\frac{f(x+h,x)-f(x,x)}{h}\)の h→0 のときの極限です。
f(x,y) に y=x を代入すると f(x,x) となるので、 これを x で偏微分すると合成関数の微分により、
\(f(x,x)_x = f_x(x,x)+f_y(x,x)\)となります。 だから、\(f(x,x)_x\) と \(f_x(x,x)\) とは意味が違います。 limit を使って言えば、\(f(x,x)_x\) は
\(\displaystyle\frac{f(x+h,x+h)-f(x,x)}{h}\)の h→0 のときの極限です。
基礎数理 II は、2007 年度入学者から 基礎数理 III と内容が入れ替わりました。 よって、2006 年度以前の入学者にとっては、 基礎数理 II、III は 2008 年度から読み替え科目になります。
よって、
基礎数理 II は、2007 年度入学者から
基礎数理 III と内容が入れ替わりましたので、
それ以降この質問が出るようになりました。
これは、以前の基礎数理 II (現在の基礎数理 III) の
QandA のページ
の
回答 (Q.1)
を参照してください。
(10/09 2008)
例を使って説明します。 ただし、以下では A/B は「B 分の A」、 A/BC は「BC 分の A」 という分数を意味することとします。
部分分数分解は通分の逆であり、例えば (2x-5)/(x+2)(x-1) という分数に対して、
\(\displaystyle \frac{2x-5}{(x+2)(x-1)} = \frac{A}{x+2} + \frac{B}{x-1}\) ... (1)となるような A, B を求める問題になるわけですが、 これを解く場合、(1) の分母を払って、
\(2x-5 = A(x-1) + B(x+2)\) ... (2)として、ここから A, B を求めます。 その方法はいくつかありますが、 例えば、以下のようなものが代表的な方法です。
この質問は、この後者の方法に関するもので、 x=1 を代入すれば -3 = 3B より B=-1, x=-2 を代入すれば -9 = -3A より A=3 と簡単に求まるのですが、 この「簡単に求めることのできる x=1, x=-2 という値は、 そもそも (1) の分母が 0 になってしまうものなので、代入してはいけないのでは」 というのが質問の意図だと思います。
まず結論から言えば、これらの値を代入しても構いません。 その理由を、極限の考え方を用いて数学的に説明します。
(1) の式は確かに x=-2, x=1 は代入できない式ですが、 それ以外のすべての x で成り立たなければいけない式です。 よって (2) も、とりあえずは x=-2, x=1 以外のすべての x で成り立つべき式です。
ところで、この (2) の両辺はいずれも単なる多項式ですから、 x=-2, x=1 も込めて連続関数であり、 左辺を f(x) (= 2x-5)、 右辺を g(x) (= A(x-1) + B(x+2)) とし、 例えば x=1 の方を考えますと、
ということが言えます。この 1., 2., 3. により、 f(1)=g(1) が成り立つことが言えます。 すなわち、(2) が x=1 でも成り立つことになるので、 x=1 を代入しても構わないわけです。
分母を払った式は、
確かに元々分母が 0 になるような x の値に対しては
成り立たないわけですが、
その点以外のその点の近くでは成り立っていて、しかも連続なので、
その点でも成り立つことになる、という仕組みです。
ということで、もっと複雑な場合の部分分数分解でも同様で、
元の式の分母が 0 になる x の値でも、
分母を払った式に代入して構いません。
(03/06 2009)
指数、対数の良い例題だとも思いますので、説明しましょう。
私の関数電卓は、指数部が 2 桁までなので、最大で表示できる実数は \(9.999999999\times 10^{99}\) までなので、 \(e^n\) は n=230 までしか出ません。 それは、電卓で \(\log_e(9.999999999\times 10^{99})\) の値を計算すればわかりますが、これは 230.258... です。 よって、\(e^{230.258\ldots} = 9.999999999\times 10^{99}\) なので、これより大きい \(e^{231}\) は表示できないわけです。
ではどうしたらよいかということですが、まず、 \(e^{700}\) がどれくらいの大きさか考えてみましょう。
\(e^{700} = A\times 10^n \ (1.0\leq A<10.0)\)とすると、両辺の常用対数を取れば、
\( \log_{10}(左辺) = \log_{10}e^{700} = 700\times \log_{10} e\)となりますが、1.0≦A＜10.0 より
\(\log_{10}(右辺) = \log_{10}(A\times 10^n) = \log_{10}A + \log_{10}10^n = \log_{10}A + n \)
\(\log_{10}1.0 = 0\leq \log_{10}A < \log_{10}10.0 = 1\)より \(\log_{10}A\) は 1 未満の小数になります。 よって、
\(700\times \log_{10}e = \log_{10}A + n\)より、\(700\times\log_{10}e\) の整数部分が n になります。
仮に、700 の代わりに 400 でやってみましょう。 「\(400\times\log_{10}e\)」はもちろん電卓でも計算でき、 この値は「173.7177928」のようになります。 つまり、n = 173、\(\log_{10}A = 0.7177928\)、となります。 この値から元の A の値を求めるには、 \(A = 10^{0.7177928}\) とするだけですから、 これも電卓で求まります。
実際には、上で求めた「\(400\times\log_{10}e\)」から 173 を引いて、 それに対して \(10^x\) という計算をやるだけです。 結果として 5.221469674 と求まります。 これで、結果として
\(e^{400} = 5.221469674\times 10^{173}\)であることになります。
電卓の使い方だけわかればよいわけではなく、
指数法則や対数法則を知ることも大事であることが
この例からもわかりますね。
(11/19 2014)
具体的には、復習問題の際に手書きの正答例を配布していますが、 その中にある、私の手書きの「π」の文字がわかりにくい、 というものでした。確かにそのπは右側の縦線が少し真っ直ぐに 下に長く伸びていたので、πには見えにくかったかもしれません。
しかし、逆にその質問用紙に書かれていた質問者の「5」の文字は、
かなり「5」には見えづらいです (「ζ」のような「5」)。
つまりこの例からもわかりますが、
他人に取って見えにくい、ということは自分ではわかりにくい、
ということです。
よって、注意したいとは思いますが、
本人の努力では限界があります。
もし見えにくい文字があったらその場で指摘してください。
(12/07 2016)
通常、高階導関数は、階数が少なければ \(y'\), \(y''\) などと書きますが、 階数が多くなると \(y^{(4)}\), \(y^{(5)}\) などと書きます。 階数が多い場合 ' を重ねて書かれたのはすぐにはわかりにくいですし (数えなければいけない)、 狭いところにはあまりうまくは書けなくなります。 実際質問者も窮屈そうに '''' を書いています。
もちろん間違いしではないし、何階導関数からは \(y^{(n)}\) と書く、
と決まっているわけではありませんので、\(y''''\) と書いても構いませんが、
注意が必要です。
自分のノートに書く分にはどう書こうが全く問題ありませんが、
試験の答案の場合は、それは採点者に見せるためのものなので
読む人がわかりにくい記号では書かないようにするのが自然でしょう。
中途半端に消しゴムで消していたりするとさらにあいまいな答案となり、
もしかすると減点されてしまうかもしれません。
(12/07 2016)
数学の答案では、基本的には認められません。
まず「極大値」と「最大値」が違うことを認識してください。 ひとつの関数に「極大値」が複数存在することがありえますが、 「最大値」は一番大きな値ですから、ひとつの関数にはひとつしかありません 最大値が極大値でない場合もあります。
そして、一般的には「max」「min」は、むしろ 「最大値」「最小値」を表すものとして使用されることが多いので、 「max」「min」で「極大値」「極小値」を表すとは通常はみなしません。 数学以外ではそもそも「極大値」「極小値」という言葉はほとんど使いません。
では、数学の分野ならいいか、というとそれもだめです。 最大値、最小値、極大値、極小値は、英語では以下のように言います。
見てわかるように、「max」とだけ書いても、
それが「最大値」を指すか「極大値」を指すかが確定しません。
よって数学の分野でも「極大値」を「max」とは書きません。
(12/27 2016)
これは、多分 3 次関数 f(x) に対して、 f'(x)=0 の実数解が 2 つあったときに、 f'(x) の符号が ＋，−，＋ になるか、 または −，＋，− になるかのいずれかで、 それは f(x) の \(x^3\) の係数が正か負かで分かれる、 という話だと思います。
その符号をそのように判断してもいいか、という話であれば、 「3 次関数に限って言えば、それは問題ない」と言えるでしょう。 そのように高校で学んだとも書いてありましたが、 高校の数学 II では微分は 3 次関数までしかやりませんので、 そういう対策を教わったのだと思います。
しかし、通常の微積分では 3 次関数以外の関数も扱いますし、 その場合には単純に係数で決まるわけではありません。 よって、講義で説明したように f'(x) の因数分解をした式から考える、 あるいはその範囲の 1 点の値で考える、という手法が必要になります。
例えば、f(x) が 5 次関数で、
\(f'(x) = (x-3)(x-1)^2(x+1)\)だった場合、f'(x) = 0 となる x は x = -1, 1, 3 ですが、 その増減表は以下のようになります。
| x | … | -1 | … | 1 | … | 3 | … |
|---|---|---|---|---|---|---|---|
| f'(x) | ＋ | 0 | − | 0 | − | 0 | ＋ |
| f(x) | ／ | ＼ | ＼ | ／ |
単純に ＋，− が交互に現れる場合ばかりとは限りません。
(12/27 2016)
商の微分は、微分の公式でも最も複雑なものの一つで、 確かにかなりごちゃごちゃになります。 計算間違いをすることが多いとも書いてありましたが、 それを避けるには、以下のようにするのがいいのではないかと思います。
狭いスペースで計算しようとすると、式が途中で折れ曲がったり、 字が小さくなったりして、自然に見にくくなってきます。 答案であれば、裏を使うなどして、 広いスペースを使うことで、 まっすぐな見やすい式を書くことができます。
計算間違いのうち、暗算が占める割り合いは大きいのではないかと思います。 そして、暗算で計算した場合は、それを見直すことができません。 だから、なるべく暗算ではなく、紙の上で計算することで、 目で確認しながら計算するのが重要です。 紙の上に書けば、ちゃんと見直すこともできます。
そして、紙の上に計算をちゃんと残すためには、 1. の広いスペースも必要になるでしょう。
商の微分のように、複雑な公式の場合は公式の覚え間違い、 使い間違い、という間違いもかなりあります。 それを防ぐには、 まず簡単な関数、例えば \(x^5/x^2\) のような商で 「記憶の公式」が合っていることを確認するといいでしょう。 その結果が \((x^3)'=3x^2\) になれば OK です。
自分の計算を見直しながら再計算してみることも重要だと思います。 特に、ものを作るために必要な計算など、 どうしても間違えてはいけない計算の場合は、 その結果を複数回見直す必要があるでしょう。
ちなみに、私は見直す必要がある場合は、 それを別な方法でも計算してみたり、 あるいは問題の設定から 値がだいたい適切なのかを考えてみたりしています。 また、計算と見直しを同時に行う (見直しながら計算する) ことも多いように思います。
私は確かに「問」を急いで書くときは、特に門がまえの部分を
「
」
と書きますが、それに関する意見だと思います。
これは単なる略字で、特に理由はありません。
楽だからそう書いているだけです。
急いでいるときには便利ですし、 わかっていれば他の文字と誤解はほとんどないでしょうし、 割と広く使われているものなので、 そういうものだということを知っておくのも悪くはないと思います (それも勉強の一つ)。
なお、この門がまえの略字は、門がまえの行書、 草書の書き方から来ているようです。 さらに、現在の中国 (本土) で使われている漢字 (簡体字) では、 門がまえはほぼこの書き方に近い門がまえが使われています (中国の簡体字の場合は中の棒が左側に点として書かれる)。
これらの理由であまり積極的に直そうとは思わないですが、 余裕があるときは丁寧に書きたいと思います。
ちなみに、異体字、略字などは特に手書きではたくさん使われています。 例えば以下を参照してみてください (もちろんこの略字も載っています)。
「高校で習ったやり方」は、u を書かずに、例えば \(y=5(4x-1)^{-2}\) の微分を
\(y' = -2\times 5(4x-1)^{-3}\times(4x-1)' = -10(4x-1)^{-3}\times 4 = -40(4x-1)^{-3}\)という風に書くことのようですが、 これはこれで構いません。
ただし、合成関数の微分を使っていることがわからないような 暗算の多い答だけの答案 (この手の解き方に多い) だと減点する可能性があります。
また、今後面倒臭い、複雑なものが出てくることを考えると、
ちゃんとどういう微分の公式を使っているかを
自分でも確認できる方法で書く方が望ましいでしょう。
意識せずに使っていると、
少し従来と違うパターンの問題で間違える可能性が高くなります。
(10/24 2018 更新)
「別の書き方」として書かれていたのは、 具体的には「\(2e^x(2+x)\)」と「\(2(2+x)e^x\)」 でしたが、どう書いたらよいかを少し詳しく書きます。
\(4e^x+2xe^x,\ (4+2x)e^x\)
\(2xe^x+4e^x,\ (4+2x)e^x,\ (2x+4)e^x\),
\(2(2+x)e^x,\ 2(x+2)e^x\)
\(4e^x+2e^x x,\ 2e^x x+4e^x,\ e^x(4+2x),\ e^x(2x+4)\)
\(2e^x(2+x),\ 2e^x(x+2)\)
\(e^x 4+e^x 2x,\ e^x4+e^x x2,\ e^x 2x+e^x4,\ e^x x2+e^x 4\),
\((2+x)2e^x,\ (x+2)2e^x,\ (2+x)e^x 2,\ (x+2)e^x 2\),
\(e^x 2(2+x),\ e^x 2(x+2),\ e^x(2+x)2,\ e^x(x+2)2\)
\((2x+1)\sin x,\ (2x+1)\log_e x\)これを以下のように書いてはいけません。
\(\sin x (2x+1),\ \log_e x(2x+1)\)これは、sin や log の中に入っているのが x なのか x(2x+1) なのかの判別がつかなくなるからです。
\((\sin x)(2x+1),\ (\log_e x)(2x+1)\)のようにかっこを書けばその判別はつくのですが、 多項式を前に出せばそのかっこは不要になります。
2020 年度以降、講義の Web ページは Moodle が主になり、 そちらにその年度に受けた質問と回答を QandA のセクションに書きました。 それらをこちらに改めてまとめておきますが、 特に整理はしませんし、あくまで当時の回答なので、 現在にはあてはまらない回答もあるかもしれません。
(10/03 2022)1. XX がわからない。(2020-10-13)
→ そのために教育センターがあります。 または、理解していないことなら復習して理解を試みる、 覚えるしかないことなら問題を解いて身につける、といった感じでしょうか。 私のホームページの方にある「大学の講義について」 (lecture.pdf) の 3 ページの 1 から 5 も参考にしてみてください。
2. 学生証を忘れて出欠登録をしなかった。(2020-10-20)
→ 最初の講義のときにも説明しましたが、 この講義は出席用紙で出欠を取りますので、 学生証をかざさなくても出席用紙を提出すれば出席とします。 逆に提出しなければ欠席とします。
3. ならば最初から学生証による出欠登録はしなくてよいか。(2020-10-27)
→ 紙だと遅刻を知ることはできませんし、 システム側の出欠訂正が大変になるので、学生証の登録も行ってください。
4. いつまで高校の内容をやっているのか。(2020-10-28)
→ 高校の内容といっても、数 I, 数 II だけ学んだ学生もいれば、 数 III や数 A, 数 B を学んだ学生もいるので、 一概にここまでが高校の内容と分けることはできません。 逆に、そういう状況だからこそ、大学で必要な共通部分を確実にするために、 主に高校の内容を復習しているとも言えます。
なお、現在の基礎数理 II(b) の教科書は、 高校の数学 II、数学 III の内容に含まれるものが多いですが、 §1.4 や 4 章の半分ほど、および 6 章は高校ではやらない内容です。 退屈ならば、そのあたりを自分で予習してみたらいかがでしょうか。
5. 小テストの結果はいつわかるか。(2020-11-09、2020-12-19)
→ 例年は採点と集計が済み次第、答案を返却していたのですが、 今年は答案を返却しづらい状況です。 どのようにフィードバックできるか今検討中ですが、 前期のレポートの採点結果と同様、結果を知らせない、 ということになるかもしれません。
→ 初回の小テストの点数を、 10 週目のところに課題形式でフィードバックのところに記載しています (冬休み前まで)。
6. \(\int -2xdx\) と書くと引き算に見える、と言っていたが、 引き算の式として成立するのか。(2020-12-19)
→ 確かに「\(\int\)」が変数や数値ではない以上、 引き算としては、意味がなくなると思います。 ただ、逆に引き算に見える場合、そこに意味があるかもしれない、 と考えてしまうのが問題です。 特に手書きだと「\(\int\)」は「\(Ｓ\)」や 「\((\)」のように見えるように書いてある場合もあるので、 そういう誤解は増えます。
また、意味がないから誤解はないからそういう書き方をしていいかといえば、 実際の本ではそんな風に書かれていることはほとんどありません。 誤解を招くような書き方をせず、正しい書き方を身につけるべきだと思います。
1. 椅子の上に座布団のようなものがあるが (講義室 12)。(2021-11-08)
→ それは大学で用意したもので、そのまま使ってください。 それがある場所に座るように、という目印にもなっているそうです。 現在、座る部分がクッションになってない講義室 3,12,13 に備えつけられているそうです。
2. ある場所の机ががたついているので直して欲しい (講義室 6)。(2021-11-09)
→ 今回は私が直しておきましたが、工学部の学生なら自分で直しましょう。 ヒントは、机の足の下にある白いネジです。
3. \((4+2x)e^x\) という解答は、別の書き方でもよいか。 (2021-11-22)
→ 以下をご覧ください。
4. 復習問題で、時間がかかる問題の場合は時間を延長してもらいたい。(2021-11-29)
→ 復習問題の分量は、問題数ではなく、私が実際に解いた時間で決めています。 よって、本来「時間がかかる問題の場合」はないはずで、 初回の復習問題も今の復習問題も同じくらいの時間で終わるはずです。
そうならないのは、その内容の復習がちゃんとできておらず、 解く際に考える時間が必要だからでしょう。 むしろ、時間が足りない場合は、そういう目安になります。 その場合はあらためて充分に復習をしてください。
ちなみに復習問題の分量は「私が解いて 2 分半から 3 分弱程度」としています。
1. アークコサインの問題では、\(0\leq\theta\leq\pi\) と書くのと \(\theta\in[0,\pi]\) と書くのはどちらでもよいのでしょうか。(2022-10-11)
→ 同じ意味なので、どちらでも結構です。
2. \((1+1/n)^n\) の極限が、2.718... のような数字になる理由がわかりません。 (2022-11-01)
→ \(1+1/n\) が 1 に収束するので、
\(1+1/n\) は全体を 1 に近づけようとする、ということはわかった、
ということでしたが、例えば、これが \((1+1/n)^{10}\) であれば、
これは n が大きくなれば \(1^{10}=1 \) に収束します。
10 の代わりに 100 でも 1000 でも、指数が定数ならば、
どんなに大きな指数であっても 1 に収束します。
一方、\((1+1/10)^n\) であれば、これは \(1.1^n\) で、
底が 1 より大きい指数関数なので
n が大きくなれば限りなく大きくなって無限大になります。
\((1+1/100)^n\) でも \((1+1/1000)^n\) でも同じく無限大になります。
それに対して e の定義の式は、\((1+1/n)^n\) の形で、
同時に両方の n が動くので、
1 に近づけようという効果と無限大にしようという効果がぶつかって、
そのため中間の 2.7... という数字に収束するのです。
例えば n=1000 のときは、\((1+1/1000)^{1000}\) となって、
底もかなり 1 に近いのですが、指数もかなり大きいので、
1 と無限の間の 2.71692... のような値になります。
実際に、それが有限な値に近づくこと、
およびそれが 2 と 3 の間であることは、
教科書 p12 にも説明が書いてありますが、少し難しいです。
3. 8週目の復習問題で、(2) の定数 \(2\log_e7\) の微分は消えるのに、 (4) の定数 \(3\log_e 10\) の微分が消えないのはどうしてですか。(2022-11-15)
→ (2) の定数は単独の定数ですが、(4) の定数は単独の定数ではなく、 「定数倍」です。\(5x^2+3\) の微分が \(5\cdot 2x\) になるのと同じです。 5 は定数倍なので 5 倍が残りますが、3 は単独の定数なので微分は 0 です。 一般には、\((cf(x))'=cf'(x)\), \((c)'=0\) です。
4. 10週目の復習問題の [2](5) で、A=1/2.12 なのに、 f(x)≒(1/2)-(1/4)(x-2)に代入しているのが 2.12なのはなぜですか。(2022-11-29)
→ x=2.12 を代入するのか、x=1/2.12 を代入するのかがわからない、
ということでしょうか。
f(x)=1/x であることから、この近似式は
「\(\frac{1}{x}≒\frac{1}{2}-\frac{1}{4}(x-2)\ (x≒2 のとき)\)」
というものになります。
こう見れば、代入すべきものが x=2.12 なのか
x=1/2.12 なのかは明かでしょう。
x=1/2.12 なら、左辺は 2.12 になってしまいますが、
求めたいのは「2.12 の近似値」ではなく、
「1/2.12 (=f(2.12))」の近似値です。
それに、この近似式は「x≒2」のときにしか使えません。
x=2.12 は 2 に近いですが、x=1/2.12 は 2 に近くはありません。
だから、x=1/2.12 は代入できません (代入しても≒にはならない)。
5. 数学における「定義」と「定理」はどう違うのですか。(2022-12-13)
→ 「数学における」とありましたが、日常語でも使われますので、
その違いは知っておくべきです。
用語としては、中学2年生あたりで学ぶもので、
中学生の教科書を見ると、以下のように書かれています。