DiPerna 流 ([4],[5]) のやり方では、
この
![]() の最も大きな項の極限が「Young 測度の微分」になることを示し、
それが 0 であることから
の最も大きな項の極限が「Young 測度の微分」になることを示し、
それが 0 であることから ![]() 以外にはサポートがないことを言うのであるが、
「測度の微分」はややとっつきにくいので、
ここでは (47) を利用し、
Lions ら ([6]) の方法のように
以外にはサポートがないことを言うのであるが、
「測度の微分」はややとっつきにくいので、
ここでは (47) を利用し、
Lions ら ([6]) の方法のように
![]() に
に ![]() をかけて
をかけて ![]() で積分することで、
で積分することで、
![]() 以外にはサポートがないことを直接示すことにする。
以外にはサポートがないことを直接示すことにする。
命題 13 で ![]() を分割したが、
まずは
を分割したが、
まずは ![]() の積分から考えることにする。
そのために、
の積分から考えることにする。
そのために、![]() をさらに 2 つに分け、
をさらに 2 つに分け、
同様に、![]() の積分は、
の積分は、
よって、
![]() に対して
に対して
同様に ![]() ,
, ![]() と
と ![]() の積の積分を考えると、
の積の積分を考えると、
![]() の方は、
の方は、![]() の
の ![]() がなく、
がなく、![]() が
が ![]() と
なっているだけなので、
と
なっているだけなので、
残りの ![]() は
は ![]() であるから、Lebesgue 有界収束定理により、
であるから、Lebesgue 有界収束定理により、
![]() に対し、次が成り立つ。
に対し、次が成り立つ。
この命題 14 により、 Fubini の定理、Lebesgue 有界収束定理を用いれば
(48)
(49)
(50)
![]() は、
は、
![]() となる測度
となる測度 ![]() と
と
![]() なる
なる ![]() によって
によって
(51)
証明
まず、![]() が 0 でないように
が 0 でないように ![]() ,
, ![]() が取れることを示す。
が取れることを示す。
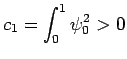 とすれば
とすれば
(52)
この命題 15 の証明で ![]() ,
, ![]() が使われていて、
ここでは
が使われていて、
ここでは
![]() としたが、
としたが、
![]() であればよいので、
そのような
であればよいので、
そのような ![]() ,
, ![]() はこれ以外にも無数にある。
このように
はこれ以外にも無数にある。
このように ![]() ,
, ![]() に対する制限が緩いのは、
8 節で述べたように (44) を用いることで、
に対する制限が緩いのは、
8 節で述べたように (44) を用いることで、
![]() ,
, ![]() への強い仮定を置かずに
への強い仮定を置かずに
![]() を示すことができたからにほかならない。
を示すことができたからにほかならない。
さて、最後にこの命題 15 の ![]() が 1 であることを示そう。
もしこれが言えれば、
が 1 であることを示そう。
もしこれが言えれば、![]() は全測度 1 であるから
は全測度 1 であるから
今、(40) に (51) を適用すると、![]() は
は ![]() 上 0 であるので、
上 0 であるので、
この命題 16 と 4 節の性質 2., 4. を用いれば、その極限 ![]() が (3), (4) のエントロピー解であることは容易に示される。
が (3), (4) のエントロピー解であることは容易に示される。
竹野茂治@新潟工科大学