11 最後に
本稿では、補償コンパクト法の DiPerna 流の方法 ([4],[5]) を改良したものと Lions らの方法 ([6],[8]) を合わせた形で、
簡単な 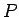 に対する 1 次元理想気体のエントロピー解の存在 (近似解の収束) を示す方法の概要を紹介したが、
本稿で工夫した方法については、
に対する 1 次元理想気体のエントロピー解の存在 (近似解の収束) を示す方法の概要を紹介したが、
本稿で工夫した方法については、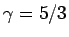 だけでなく、
(2) のすべての
だけでなく、
(2) のすべての 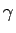 についても同様のことが行えることがわかっている。
についても同様のことが行えることがわかっている。
それを、[4] のように
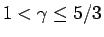 にまで拡張できるかどうかはまだ確認はしていないが、可能性はあるだろうと思う。
しかも本稿の方法であれば、[4] の
にまで拡張できるかどうかはまだ確認はしていないが、可能性はあるだろうと思う。
しかも本稿の方法であれば、[4] の 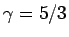 の壁を越えて、
の壁を越えて、
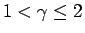 にまで拡張できるのではないかと予想しているが、
その場合は
にまで拡張できるのではないかと予想しているが、
その場合は
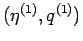 が有界にはならないので本稿の論法には多少変更が必要となる。
それには
が有界にはならないので本稿の論法には多少変更が必要となる。
それには 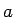 に関する可積分性を利用して、
(47) を最終的に使用する (49) の
に関する可積分性を利用して、
(47) を最終的に使用する (49) の
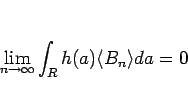
に変えればなんとかなるのでは、と考えているが、
ただ、
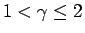 の場合は、
1 節でも述べたように [6] で解決しているので、
それが言えたとしてもあまり意味はないだろうと思う。
の場合は、
1 節でも述べたように [6] で解決しているので、
それが言えたとしてもあまり意味はないだろうと思う。
竹野茂治@新潟工科大学
2010年1月6日
![]() にまで拡張できるかどうかはまだ確認はしていないが、可能性はあるだろうと思う。
しかも本稿の方法であれば、[4] の
にまで拡張できるかどうかはまだ確認はしていないが、可能性はあるだろうと思う。
しかも本稿の方法であれば、[4] の ![]() の壁を越えて、
の壁を越えて、
![]() にまで拡張できるのではないかと予想しているが、
その場合は
にまで拡張できるのではないかと予想しているが、
その場合は
![]() が有界にはならないので本稿の論法には多少変更が必要となる。
それには
が有界にはならないので本稿の論法には多少変更が必要となる。
それには ![]() に関する可積分性を利用して、
(47) を最終的に使用する (49) の
に関する可積分性を利用して、
(47) を最終的に使用する (49) の