9 到達時間の比較
この節では、7 節で最後に述べた、
いくつかの解に対する到達時間 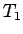 ,
, 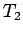 ,
, 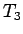 の比較を行う。
まず
の比較を行う。
まず 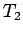 ,
, 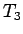 の式を求める。
の式を求める。
7 節でみたように、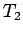 は
は
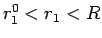 ,
,
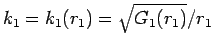 に対し
に対し 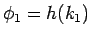 としたものに対する (31) の形の解の
到達時間が
としたものに対する (31) の形の解の
到達時間が 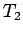 であるが、
であるが、
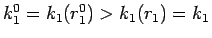 より、
命題 1 により
より、
命題 1 により
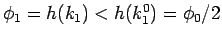 となるので、
確かに
となるので、
確かに
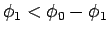 となっていることがわかる。
となっていることがわかる。
この
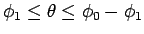 の間では
の間では 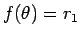 、
すなわち円運動となるが、その間は向心力と垂直抗力の
いずれも半径方向の力だけが働くので、等速円運動となる。
実際、半径
、
すなわち円運動となるが、その間は向心力と垂直抗力の
いずれも半径方向の力だけが働くので、等速円運動となる。
実際、半径 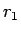 の円運動の加速度は、
の円運動の加速度は、
であるが、力は
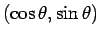 に平行にしか働かないので、
に平行にしか働かないので、
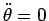 であり、よって角速度
であり、よって角速度
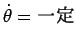 の
等速円運動となる。
の
等速円運動となる。
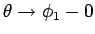 では、曲線は丁度半径
では、曲線は丁度半径 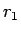 の円に接し、
そのときの速度ベクトルも円に接する。
よって、その到達時の速さが円運動の速さに一致する。
その速さ
の円に接し、
そのときの速度ベクトルも円に接する。
よって、その到達時の速さが円運動の速さに一致する。
その速さ 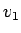 は、エネルギー保存則 (4) から
求めることができ、
は、エネルギー保存則 (4) から
求めることができ、
より、
となり、角速度 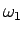 は
は
となる。
よって
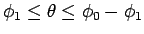 でかかる時間は
でかかる時間は
となる。
今、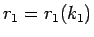 に対して、
に対して、
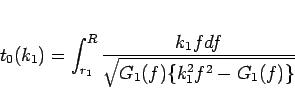 |
(41) |
と書くことにすれば、(31) の
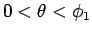 までに
かかる時間は (30) により
までに
かかる時間は (30) により
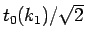 であり、
であり、
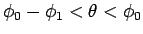 の部分も同じなので、結局
の部分も同じなので、結局 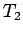 は、
は、
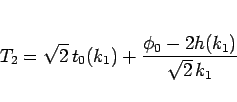 |
(42) |
となる。
同様に 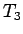 は、
は、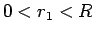 に対して
に対して 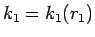 ,
,
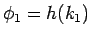 に対する (32) による解がかかる
時間であるから、上と同様にして
に対する (32) による解がかかる
時間であるから、上と同様にして
となることがわかる。
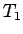 は (30) と
は (30) と
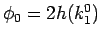 により
により
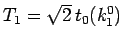 であり、
(42) で
であり、
(42) で
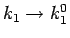 とすれば
とすれば
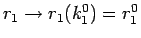 となるので
となるので
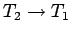 となる。
となる。
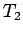 では
では 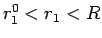 より
より 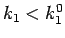 であるから、よって
であるから、よって
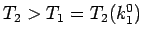 を示すには、
を示すには、
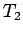 の
の  に関する単調減少性を示せばよい
に関する単調減少性を示せばよい
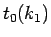 を少し変形すると、
を少し変形すると、
となる。この最後の式の最初の項を 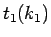 と書くことにする。
と書くことにする。
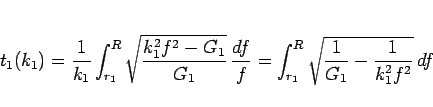 |
(44) |
これにより、
となる。
さて、(44) より  は特異性を持たず、
よって
は特異性を持たず、
よって  を微分すると
を微分すると
となるが、この最初の項は (12) より 0 になるので、
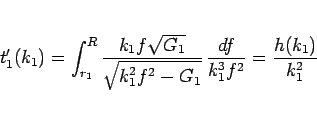 |
(48) |
となることがわかる。
(46), (48), および
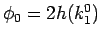 より、
より、
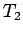 を
を  で微分すると
で微分すると
となるが、命題 1、および 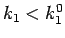 より
より
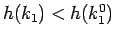 なので、よって
なので、よって 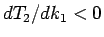 であることがわかる。
これで
であることがわかる。
これで 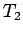 の減少性が言えて、
の減少性が言えて、
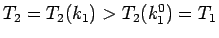 が言えたことになる。
が言えたことになる。
次は 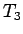 と
と 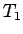 を比較する。
を比較する。
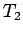 の場合と違い
の場合と違い 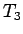 では
では  には制限はなく、
には制限はなく、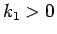 であるが、
(47), (48) より、
であるが、
(47), (48) より、
となる。ここで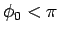 で、
命題 1 より
で、
命題 1 より 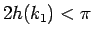 なので、
なので、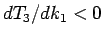 となる。
よって、
となる。
よって、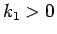 に対して、
に対して、
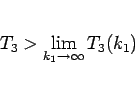 |
(49) |
となる。ここで、(44)、及び
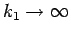 の
とき
の
とき
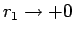 により
により
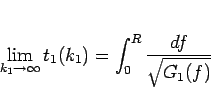 |
(50) |
が言える (厳密には定理 2 で証明できる)。
よって、(47) より
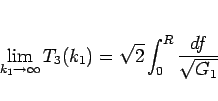 |
(51) |
となる。
なお、この右辺の積分は、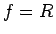 で特異性を持つが、
で特異性を持つが、
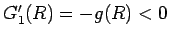 より有限である。
より有限である。
一方、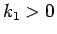 に対して、(48) より
に対して、(48) より
となるから、命題 1 より 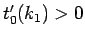 で、よって
で、よって
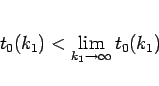 |
(52) |
となるが、命題 1、および (50) より
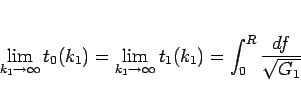 |
(53) |
がわかる。よって、(45), (49),
(51), (52), (53) より、
が言えたことになり、
これで任意の 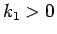 に対して
に対して 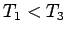 も示されたことになり、
途中に円の一部をはさむもの
も示されたことになり、
途中に円の一部をはさむもの 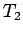 ,
, 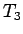 よりも
よりも 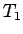 の方が速いことが示されたことになる。
の方が速いことが示されたことになる。
竹野茂治@新潟工科大学
2017年2月24日
![]() は
は
![]() ,
,
![]() に対し
に対し ![]() としたものに対する (31) の形の解の
到達時間が
としたものに対する (31) の形の解の
到達時間が ![]() であるが、
であるが、
![]() より、
命題 1 により
より、
命題 1 により
![]() となるので、
確かに
となるので、
確かに
![]() となっていることがわかる。
となっていることがわかる。
![]() の間では
の間では ![]() 、
すなわち円運動となるが、その間は向心力と垂直抗力の
いずれも半径方向の力だけが働くので、等速円運動となる。
実際、半径
、
すなわち円運動となるが、その間は向心力と垂直抗力の
いずれも半径方向の力だけが働くので、等速円運動となる。
実際、半径 ![]() の円運動の加速度は、
の円運動の加速度は、
![]() では、曲線は丁度半径
では、曲線は丁度半径 ![]() の円に接し、
そのときの速度ベクトルも円に接する。
よって、その到達時の速さが円運動の速さに一致する。
その速さ
の円に接し、
そのときの速度ベクトルも円に接する。
よって、その到達時の速さが円運動の速さに一致する。
その速さ ![]() は、エネルギー保存則 (4) から
求めることができ、
は、エネルギー保存則 (4) から
求めることができ、
![]() は、
は、![]() に対して
に対して ![]() ,
,
![]() に対する (32) による解がかかる
時間であるから、上と同様にして
に対する (32) による解がかかる
時間であるから、上と同様にして
![]() は (30) と
は (30) と
![]() により
により
![]() であり、
(42) で
であり、
(42) で
![]() とすれば
とすれば
![]() となるので
となるので
![]() となる。
となる。
![]() では
では ![]() より
より ![]() であるから、よって
であるから、よって
![]() を示すには、
を示すには、
![]() の
の ![]() に関する単調減少性を示せばよい
に関する単調減少性を示せばよい
![]() を少し変形すると、
を少し変形すると、
![]() は特異性を持たず、
よって
は特異性を持たず、
よって ![]() を微分すると
を微分すると
![]() と
と ![]() を比較する。
を比較する。
![]() の場合と違い
の場合と違い ![]() では
では ![]() には制限はなく、
には制限はなく、![]() であるが、
(47), (48) より、
であるが、
(47), (48) より、
![]() に対して、(48) より
に対して、(48) より