7 到達時間と負方向の解
次は、落ちて上がってくるまでの到達時間と、
負方向の解を含めた解の決定について考える。
まず、(14) に
従って落ちて上がってくるまでの到達時間 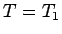 を求める。
この解では、
を求める。
この解では、
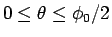 の半分までと、
残りの半分の
の半分までと、
残りの半分の
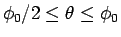 の部分は対称なので、
(7) より
の部分は対称なので、
(7) より
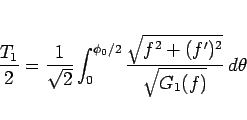 |
(29) |
となる。ここで、
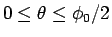 では
では
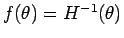 、
すなわち
、
すなわち 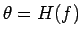 なので、これを用いて置換すると、
なので、これを用いて置換すると、
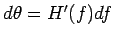 で、
で、
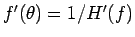 なので、
なので、
となる ( )。ここで、(9) より
)。ここで、(9) より
なので、
となり、よって 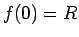 ,
,
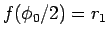 より (29) は
より (29) は
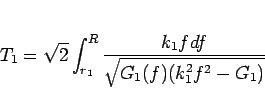 |
(30) |
となる。
(30) の式は、当然 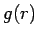 が与えられなければ計算できないが、
均質な地球の場合は計算可能である。その場合は、
が与えられなければ計算できないが、
均質な地球の場合は計算可能である。その場合は、
より、
となる。ここで、
であり、また (21),
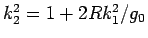 より
より
であるから、
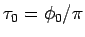 を用いれば
を用いれば
となる。よって、均質な地球の場合の到達時間は
となる。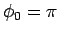 の場合は、
の場合は、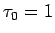 より
より
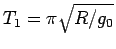 と
なるが、これは地球の直径を玉が行ったりきたりする単振動の 1/2 周期を
意味する。
地球が均質なら、重力の大きさは (2) のように
中心からの距離に比例するので、確かに単振動になる。
と
なるが、これは地球の直径を玉が行ったりきたりする単振動の 1/2 周期を
意味する。
地球が均質なら、重力の大きさは (2) のように
中心からの距離に比例するので、確かに単振動になる。
さて、微分方程式 (8) に戻ると、
これは 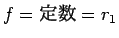 も解として持つことがわかる。
よって、(14) 以外にも、
(14) よりも少し浅いところまで降りて、
一旦一定半径の円運動をして、
そこからまた
も解として持つことがわかる。
よって、(14) 以外にも、
(14) よりも少し浅いところまで降りて、
一旦一定半径の円運動をして、
そこからまた 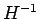 で地表まで戻るような滑らかな (8) の解
で地表まで戻るような滑らかな (8) の解
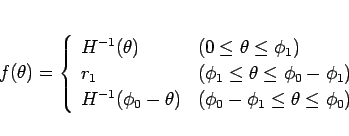 |
(31) |
があることがわかる (図 6)。
図 6:
途中の円運動を挟む解
![\includegraphics[width=7cm]{fig-cyc3-sol2.eps}](img230.gif)
|
図 7:
反対を回る解の 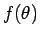
![\includegraphics[width=9cm]{fig-cyc3-sol3.eps}](img231.gif)
|
ここで、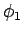 は
は
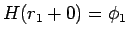 となるものであるが、
となるものであるが、
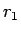 ,
,  は (14) のものとは異なる。
紛らわしいので、(14) の
は (14) のものとは異なる。
紛らわしいので、(14) の 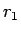 ,
,  を、
以後
を、
以後 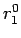 ,
, 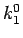 と書くことにする (
と書くことにする (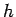 は命題 1 のもの):
は命題 1 のもの):
これに対し、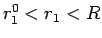 の
の 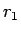 と
と
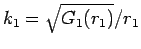 (
(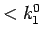 ) に対して
) に対して
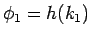 と
したのが上の
と
したのが上の 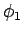 であり、(31) の
であり、(31) の 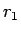 , および
, および 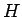 に現れる
に現れる  もこの
もこの 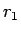 ,
,  である。
である。
さらに、前に説明した負方向に回る解もこの形で実現できる (図 7):
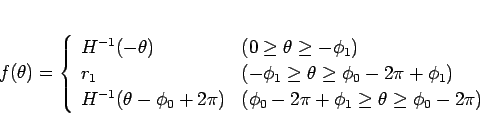 |
(32) |
この場合も
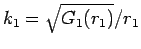 ,
,
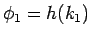 であるが、
こちらは
であるが、
こちらは 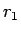 には
には 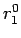 のような下の制限はなく、
のような下の制限はなく、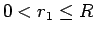 となる。
ちなみに
となる。
ちなみに
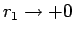 の極限は、A から中心への半径と、
中心から B への半径をつないだ (滑らかではない) トンネルになる。
の極限は、A から中心への半径と、
中心から B への半径をつないだ (滑らかではない) トンネルになる。
この (31) による解曲線での到達時間を 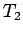 、
この (32) による解曲線での到達時間を
、
この (32) による解曲線での到達時間を 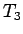 と
すると、実際に
と
すると、実際に 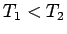 かつ
かつ 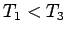 となることを 9 節で証明する。
となることを 9 節で証明する。
これにより、(14) が最速降下曲線であることが
「それなりに」保証されることになるが、
それが最速であることを [1] の 9 節のように完全に
証明するのは難しい。
竹野茂治@新潟工科大学
2017年2月24日
![]() を求める。
この解では、
を求める。
この解では、
![]() の半分までと、
残りの半分の
の半分までと、
残りの半分の
![]() の部分は対称なので、
(7) より
の部分は対称なので、
(7) より
![]() が与えられなければ計算できないが、
均質な地球の場合は計算可能である。その場合は、
が与えられなければ計算できないが、
均質な地球の場合は計算可能である。その場合は、
![]() も解として持つことがわかる。
よって、(14) 以外にも、
(14) よりも少し浅いところまで降りて、
一旦一定半径の円運動をして、
そこからまた
も解として持つことがわかる。
よって、(14) 以外にも、
(14) よりも少し浅いところまで降りて、
一旦一定半径の円運動をして、
そこからまた ![]() で地表まで戻るような滑らかな (8) の解
で地表まで戻るような滑らかな (8) の解
![]() 、
この (32) による解曲線での到達時間を
、
この (32) による解曲線での到達時間を ![]() と
すると、実際に
と
すると、実際に ![]() かつ
かつ ![]() となることを 9 節で証明する。
となることを 9 節で証明する。