4 逆関数
次は、解の逆関数に関係する関数 (9) を
少し簡単に見てみることにする。
まず、地球が均質である (2) の場合を考えると、
であるから、この場合 (9) は
となる。ここで、
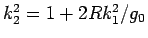 (
(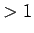 ),
), 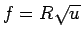 とした。
とした。
この最後の式からわかるが、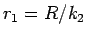 とすれば
とすれば 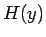 はこの場合
はこの場合 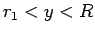 に対して値を持ち、
に対して値を持ち、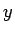 に関して単調減少で、
に関して単調減少で、
となる。この 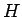 は実際に積分できて、
は実際に積分できて、
とすると
で、よって
なので、
となる。よって、
 |
(11) |
となる。
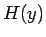 の導関数はそのまま (9) の
被積分関数の
の導関数はそのまま (9) の
被積分関数の 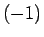 倍なので、
倍なので、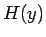 は単調減少関数で、
は単調減少関数で、
であることがわかる。
よって、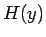 は
は ![$[r_1,R]$](img101.gif) から
から
![$[0,\pi(1-1/k_2)/2]$](img102.gif) への 1 対 1 の
関数で、その逆関数が存在する。これによって、
への 1 対 1 の
関数で、その逆関数が存在する。これによって、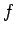 が得られることになる。
が得られることになる。
一般の 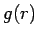 の場合も、
の場合も、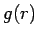 は単調増加関数で
は単調増加関数で 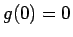 だから、
だから、
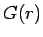 も
も 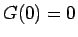 で単調増加な関数になっている。
よって
で単調増加な関数になっている。
よって
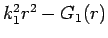 は
は 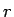 に関して増加関数で、
に関して増加関数で、
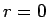 では
では 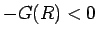 、
、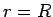 では
では 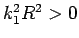 となるから、
となるから、
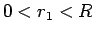 で
で
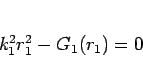 |
(12) |
となる 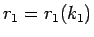 がただひとつ存在し、
がただひとつ存在し、
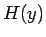 は
は 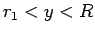 で存在することがわかる。
なお、この
で存在することがわかる。
なお、この 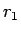 は
は  から決まるが、
逆に (12) から
から決まるが、
逆に (12) から
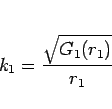 |
(13) |
により、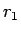 から
から  が決まると考えることもできる。
が決まると考えることもできる。
(9) より
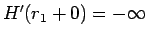 であるが、ロピタルの定理より、
であるが、ロピタルの定理より、
なので、(9) は
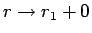 でも積分が収束し、
でも積分が収束し、
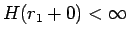 となることがわかる (図 3)。
となることがわかる (図 3)。
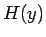 のさらなる性質はまた後で調べる。
のさらなる性質はまた後で調べる。
竹野茂治@新潟工科大学
2017年2月24日
![]() とすれば
とすれば ![]() はこの場合
はこの場合 ![]() に対して値を持ち、
に対して値を持ち、![]() に関して単調減少で、
に関して単調減少で、
![]() の場合も、
の場合も、![]() は単調増加関数で
は単調増加関数で ![]() だから、
だから、
![]() も
も ![]() で単調増加な関数になっている。
よって
で単調増加な関数になっている。
よって
![]() は
は ![]() に関して増加関数で、
に関して増加関数で、
![]() では
では ![]() 、
、![]() では
では ![]() となるから、
となるから、
![]() で
で
![]() であるが、ロピタルの定理より、
であるが、ロピタルの定理より、
![]() のさらなる性質はまた後で調べる。
のさらなる性質はまた後で調べる。