8 命題の証明
本節では、命題 1 を証明する。
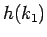 は、
は、
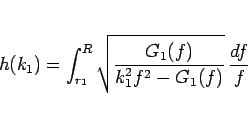 |
(33) |
であり、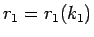 は (12) により決まるが、
逆に
は (12) により決まるが、
逆に 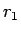 が
が  から (13) により決まるとも
見れるので、
そう見ればこの
から (13) により決まるとも
見れるので、
そう見ればこの 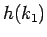 は
は 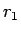 の関数
の関数 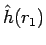 と
考えることもできる。それらは必要に応じて適宜使い分ける。
なお、
と
考えることもできる。それらは必要に応じて適宜使い分ける。
なお、
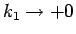 は
は
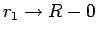 に対応し、
に対応し、
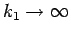 は
は
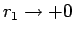 に
対応し、
に
対応し、 と
と 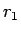 の増加方向は逆であることに注意する。
の増加方向は逆であることに注意する。
まず  を動かすと、(33) の特異性を持つ分母も
動いてしまい、極限を考えにくいので、(33) を
以下により置換する。
を動かすと、(33) の特異性を持つ分母も
動いてしまい、極限を考えにくいので、(33) を
以下により置換する。
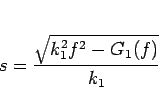 |
(34) |
これは、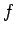 に関して単調なので、
に関して単調なので、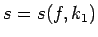 とも書けるが、
逆に
とも書けるが、
逆に 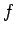 を
を 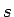 ,
,  の関数と見ることもできる。
それを
の関数と見ることもできる。
それを 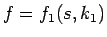 とすると、
とすると、
で、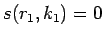 ,
, 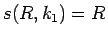 なので、
なので、
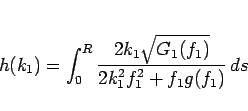 |
(35) |
となる。
まず、
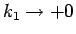 、すなわち
、すなわち
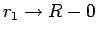 の極限を考える。
の極限を考える。
 は
は 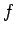 に関して増加、よって
に関して増加、よって 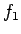 も
も 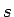 に関して増加であり、
よって
に関して増加であり、
よって 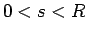 に対して
に対して
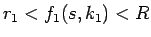 となっている。
となっている。
今、
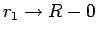 であるから、
であるから、
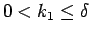 で
で 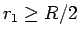 となるような
となるような 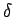 (
(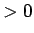 ) が取れる。
このとき、
) が取れる。
このとき、
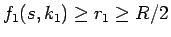 であるから、
であるから、
となり、よって (35) より
となり、右辺は
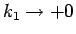 のとき 0 に収束するので、
これで (17) が示されたことになる。
のとき 0 に収束するので、
これで (17) が示されたことになる。
次は
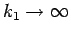 、すなわち
、すなわち
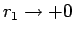 の極限を考える。
(35) をさらに
の極限を考える。
(35) をさらに 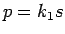 と置換すると、
と置換すると、
となる。ここで 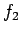 は
は 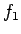 を
を 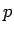 に書き換えたもの、
すなわち
に書き換えたもの、
すなわち
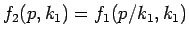 である。
(34) より
である。
(34) より
なので、
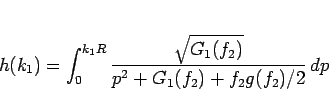 |
(36) |
となる。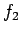 は、
は、
であるから、
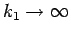 で 0 に収束する。
よって、(36) の被積分関数は
で 0 に収束する。
よって、(36) の被積分関数は
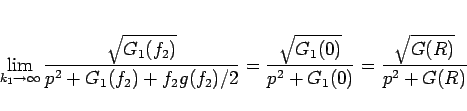 |
(37) |
に収束し、よって 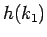 は、
は、
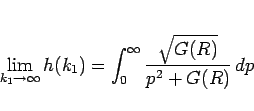 |
(38) |
となりそうである。
これが成り立つことをちゃんと示すために、次のルベーグ収束定理を用いる。
- 定理 2. (ルベーグ収束定理)
-
 上の関数
上の関数  ,
,  が、
すべての
が、
すべての 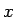 ,
, 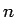 で
で
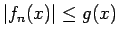 を満たし、
を満たし、
であるとき、次が成り立つ。
この定理の証明は、ルベーグ積分の適当な成書 (例えば [3]) を参照。
今、
とすると、(36) は
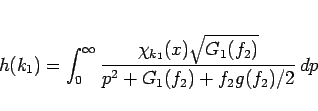 |
(39) |
となるが、
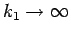 のとき
のとき
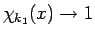 なので、
(39) の被積分関数の極限も (37) の
極限に等しい。
一方、
なので、
(39) の被積分関数の極限も (37) の
極限に等しい。
一方、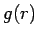 は増加関数なので、
は増加関数なので、
であり、よって
となる。
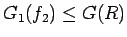 より、
(39) の被積分関数は
より、
(39) の被積分関数は
とおさえられることがわかり、この右辺は  によらず、
によらず、
となる。よって定理 2 が適用でき、
確かに (38) が成り立つことがわかる。
となるので、これで (18) も示された。
最後は、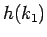 の単調性であるが、それは (36) を用いる。
(36) の分母には特異性はなく、
の単調性であるが、それは (36) を用いる。
(36) の分母には特異性はなく、
の形である。よって、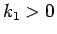 に対して
に対して 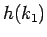 の微分は、
の微分は、
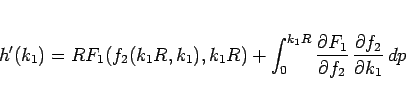 |
(40) |
となる。ここで、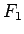 の分母を
の分母を 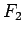 とすると
とすると
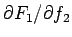 は、
は、
となるが、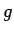 は増加関数で
は増加関数で 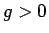 ,
, 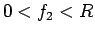 ,
, 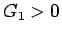 より
より
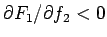 となる。また、
となる。また、
であるから  は
は 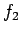 に関して減少、
よって
に関して減少、
よって
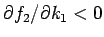 となるので、
(40) から
となるので、
(40) から 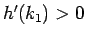 がわかる。
これで
がわかる。
これで 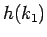 の単調性も示され、命題 1 が示されたことになる。
の単調性も示され、命題 1 が示されたことになる。
竹野茂治@新潟工科大学
2017年2月24日
![]() は、
は、
![]() を動かすと、(33) の特異性を持つ分母も
動いてしまい、極限を考えにくいので、(33) を
以下により置換する。
を動かすと、(33) の特異性を持つ分母も
動いてしまい、極限を考えにくいので、(33) を
以下により置換する。
![]() 、すなわち
、すなわち
![]() の極限を考える。
の極限を考える。
![]() は
は ![]() に関して増加、よって
に関して増加、よって ![]() も
も ![]() に関して増加であり、
よって
に関して増加であり、
よって ![]() に対して
に対して
![]() となっている。
となっている。
![]() であるから、
であるから、
![]() で
で ![]() となるような
となるような ![]() (
(![]() ) が取れる。
このとき、
) が取れる。
このとき、
![]() であるから、
であるから、
![]() 、すなわち
、すなわち
![]() の極限を考える。
(35) をさらに
の極限を考える。
(35) をさらに ![]() と置換すると、
と置換すると、
![]() 上の関数
上の関数 ![]() ,
, ![]() が、
すべての
が、
すべての ![]() ,
, ![]() で
で
![]() を満たし、
を満たし、
![]() の単調性であるが、それは (36) を用いる。
(36) の分母には特異性はなく、
の単調性であるが、それは (36) を用いる。
(36) の分母には特異性はなく、