2 設定
まず問題を以下のように設定する。
地球の半径を 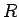 とし、地表の A
とし、地表の A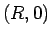 から B
から B
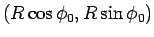 (
(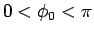 ) へ至るトンネルを考える (図 1)。
このトンネルに A から B に玉を初速度 0 で滑らすとき、
その時間
) へ至るトンネルを考える (図 1)。
このトンネルに A から B に玉を初速度 0 で滑らすとき、
その時間 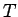 が最も短くなるようなトンネルの曲線を求めよ。
ただし、摩擦や空気抵抗は考えないものとする。
が最も短くなるようなトンネルの曲線を求めよ。
ただし、摩擦や空気抵抗は考えないものとする。
図 1:
設定
![\includegraphics[width=8cm]{fig-cyc3-ini.eps}](img8.gif)
|
図 2:
反対回りの解 ?
![\includegraphics[width=8cm]{fig-cyc3-under.eps}](img9.gif)
|
トンネルは、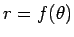 の極座標形式で考えることにする。
すなわち、
の極座標形式で考えることにする。
すなわち、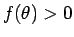 で、
で、
とパラメータ表示される曲線である。仮定より、
となる。なお、今回まずは
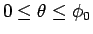 のトンネル、
すなわち反時計回りの角を進んで B に至るトンネルを考えるが、
もしかすると、中心の反対側、すなわち時計回りに角を進んで、
のトンネル、
すなわち反時計回りの角を進んで B に至るトンネルを考えるが、
もしかすると、中心の反対側、すなわち時計回りに角を進んで、
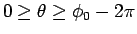 の負の角の方のトンネルが
早くなる可能性もあるかもしれない (図 2)。
それについてはまた後で考える。
の負の角の方のトンネルが
早くなる可能性もあるかもしれない (図 2)。
それについてはまた後で考える。
地中内部の 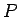 地点で質量
地点で質量 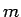 の物体に働く重力
の物体に働く重力
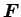 は
、地球の内部構造が同心球の層状であると仮定すれば、
[2] にあるように
は
、地球の内部構造が同心球の層状であると仮定すれば、
[2] にあるように
となる。ここで、 は、
は、 で定義される連続関数で、
で定義される連続関数で、
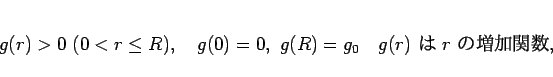 |
(1) |
となる (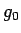 は地表での重力加速度)。
具体的には、中心から
は地表での重力加速度)。
具体的には、中心から 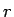 までの部分の球の質量による重力に比例する
ものになる ([2])。
簡単のため本稿では
までの部分の球の質量による重力に比例する
ものになる ([2])。
簡単のため本稿では 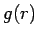 微分可能であるとする。
(1) より
微分可能であるとする。
(1) より 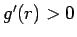 (
(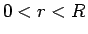 ) となる。
特に、地球内部が均質であるとすれば、
) となる。
特に、地球内部が均質であるとすれば、
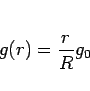 |
(2) |
と 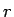 に比例する関数となる。
に比例する関数となる。
ドンネル内の動点 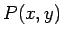 の位置ベクトルを
の位置ベクトルを
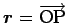 ,
,
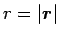 ,
, 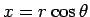 ,
, 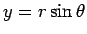 (
(
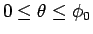 ),
),
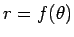 とし、トンネルからの垂直抗力を
とし、トンネルからの垂直抗力を
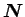 とすれば、
運動方程式は以下のようになる。
とすれば、
運動方程式は以下のようになる。
ここで 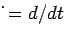 とする。
とする。
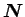 はトンネルに垂直、すなわち
はトンネルに垂直、すなわち 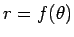 の接線方向に垂直になる。
の接線方向に垂直になる。
トンネルは 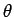 でパラメータ表示されるから、
動点の位置を
でパラメータ表示されるから、
動点の位置を 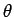 で表すことができ、
よってそれを時間の未知関数
で表すことができ、
よってそれを時間の未知関数
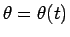 として考えることができる。
このとき、速度
として考えることができる。
このとき、速度
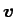 は
は
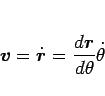 |
(3) |
であり、
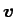 はトンネルの接線方向を向くベクトルになる。
よって、
はトンネルの接線方向を向くベクトルになる。
よって、
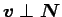 であるから、
運動方程式と
であるから、
運動方程式と
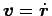 との
内積を考えれば、
との
内積を考えれば、
となるが、
となる (
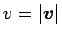 )。よって、
)。よって、
となるので、
とすれば
となり、よって
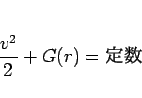 |
(4) |
が成り立つことになる。これは、エネルギー保存の式に対応する。
初速度は 0 であるから、(4) より
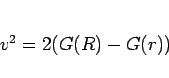 |
(5) |
となる。ここで (3) より
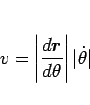 |
(6) |
であるが、
であり、
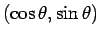 と
と
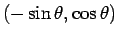 は
直交する単位ベクトルなので、よって
は
直交する単位ベクトルなので、よって
となる。
玉は 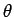 が増える方向にころがるので
が増える方向にころがるので
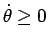 であり、
よって (6) より
であり、
よって (6) より
となり、(5), および 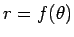 より、
より、
となるので、この式の逆数を 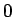 から
から 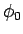 まで積分すれば、
A から B までの所用時間
まで積分すれば、
A から B までの所用時間 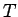 が
が
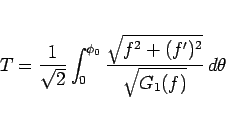 |
(7) |
と表されることになる。なお、以後
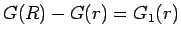 と書くことにする。
あとは、[1] と同様に、
変分法によりこの
と書くことにする。
あとは、[1] と同様に、
変分法によりこの 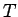 の式を最小にするような
の式を最小にするような 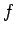 を求めればよいことになる。
を求めればよいことになる。
なお、地球の反対側を回るトンネルの場合も、
今までの議論はほぼ同じで、
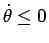 のみが異なり、
よって
のみが異なり、
よって
となるから、この逆数を 0 から 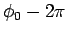 まで積分すれば、
まで積分すれば、
が得られる。
竹野茂治@新潟工科大学
2017年2月24日
とし、地表の A
から B
(
) へ至るトンネルを考える (図 1)。 このトンネルに A から B に玉を初速度 0 で滑らすとき、 その時間
が最も短くなるようなトンネルの曲線を求めよ。 ただし、摩擦や空気抵抗は考えないものとする。
![]() の極座標形式で考えることにする。
すなわち、
の極座標形式で考えることにする。
すなわち、![]() で、
で、
![]() 地点で質量
地点で質量 ![]() の物体に働く重力
の物体に働く重力
![]() は
、地球の内部構造が同心球の層状であると仮定すれば、
[2] にあるように
は
、地球の内部構造が同心球の層状であると仮定すれば、
[2] にあるように
![]() の位置ベクトルを
の位置ベクトルを
![]() ,
,
![]() ,
, ![]() ,
, ![]() (
(
![]() ),
),
![]() とし、トンネルからの垂直抗力を
とし、トンネルからの垂直抗力を
![]() とすれば、
運動方程式は以下のようになる。
とすれば、
運動方程式は以下のようになる。
![]() でパラメータ表示されるから、
動点の位置を
でパラメータ表示されるから、
動点の位置を ![]() で表すことができ、
よってそれを時間の未知関数
で表すことができ、
よってそれを時間の未知関数
![]() として考えることができる。
このとき、速度
として考えることができる。
このとき、速度
![]() は
は
![]() が増える方向にころがるので
が増える方向にころがるので
![]() であり、
よって (6) より
であり、
よって (6) より
![]() のみが異なり、
よって
のみが異なり、
よって