6 グラフ
次は、解 (14) によるトンネルのグラフを紹介する。
もちろん、一般の 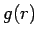 ではグラフは書けないので、
均質な地球の場合のグラフを示す。これは、
ではグラフは書けないので、
均質な地球の場合のグラフを示す。これは、
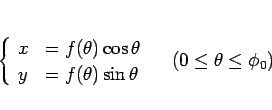 |
(19) |
で、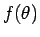 は (14), (15) より
は (14), (15) より
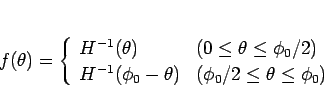 |
(20) |
であり、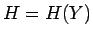 は、
地球が均質な場合は (10) より
は、
地球が均質な場合は (10) より
であった。
ここで、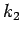 は (11), (15) より、
は (11), (15) より、
となるので、
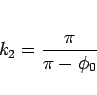 |
(21) |
である。これで、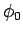 (
(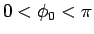 ) と
) と 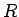 ですべて
決定できることになる。
ただし、(20) に
ですべて
決定できることになる。
ただし、(20) に 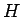 の逆関数が入っているため
グラフ化はしにくいようにみえるかもしれないが、
それはパラメータを
の逆関数が入っているため
グラフ化はしにくいようにみえるかもしれないが、
それはパラメータを 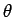 から
から 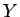 に変えれば済む。
に変えれば済む。
例えば、
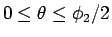 では
では 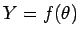 とすると、
(20) より
とすると、
(20) より
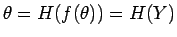 なので、
(19) を
なので、
(19) を
とすればよい (
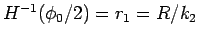 )。
さらに、
)。
さらに、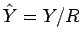 とすると
とすると
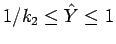 で、
で、
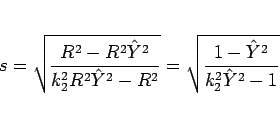 |
(22) |
となり、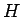 が
が 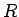 によらない式になる (それを
によらない式になる (それを
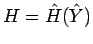 と書く)。
これによりグラフは
と書く)。
これによりグラフは
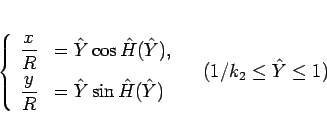 |
(23) |
となり、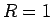 の場合のグラフ全体を
そのまま
の場合のグラフ全体を
そのまま 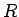 倍したものになっていることがわかる。
よってグラフとしては
倍したものになっていることがわかる。
よってグラフとしては 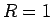 のもののみ考えればよいことになる。
のもののみ考えればよいことになる。
これで、例えば gnuplot1 の媒介変数モードを使えば、このグラフが書けるようになるのだが、
複数の 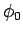 に対するグラフを一緒に書く場合には、
パラメータの範囲が一定でないのは問題があるし、
関数に特異性が含まれている (
に対するグラフを一緒に書く場合には、
パラメータの範囲が一定でないのは問題があるし、
関数に特異性が含まれている (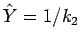 で (22) の
分母が 0 になる) とそこがうまくつながらない場合があるので、
それらを修正する。
で (22) の
分母が 0 になる) とそこがうまくつながらない場合があるので、
それらを修正する。
まずパラメータの範囲を固定するために、
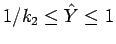 を、
を、
より、
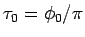 として、新たなパラメータ
として、新たなパラメータ 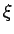 を
を
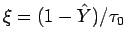 とれば
とれば 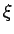 の範囲は
の範囲は
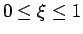 に
固定される。
そして (22), (23) に
に
固定される。
そして (22), (23) に
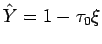 を代入すれば
を代入すれば 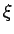 の式が得られる。
の式が得られる。
次は特異性の解消であるが、まず、
とすると、
となり、この最後の式の分母は
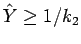 より 0 にはならない。
よって、
より 0 にはならない。
よって、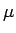 を特異性のない式
を特異性のない式
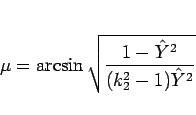 |
(24) |
に書き直すことができる。同様に、
とすると、
となり、こちらも特異性のない
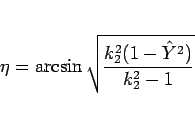 |
(25) |
と書き直せる。
この (24), (25) を、
さらに 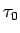 ,
, 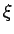 で書き直す。
で書き直す。
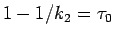 より
より
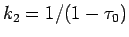 、
および
、
および
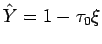 より、
より、
となる。よって、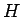 を
を 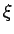 ,
, 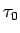 で書き表すと、
で書き表すと、
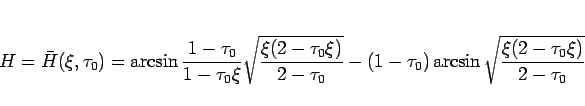 |
(26) |
となる (
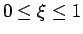 )。
)。
グラフのもう半分の
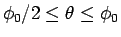 の方は、
(20) より
の方は、
(20) より
とすればよいので、結局
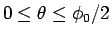 の方は、
(26) の
の方は、
(26) の
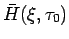 を使って
を使って
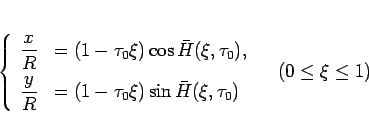 |
(27) |
と表され、
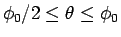 の方は、
の方は、
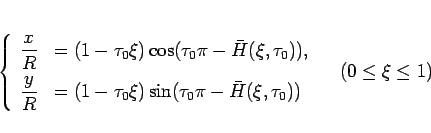 |
(28) |
と表されることになる。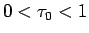 よりこれらには特異性はなく、
パラメータの範囲も固定されるので、グラフ化は難しくない。
実際、
よりこれらには特異性はなく、
パラメータの範囲も固定されるので、グラフ化は難しくない。
実際、
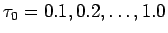 、すなわち
、すなわち
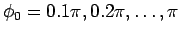 に対して gnuplot で
書いたグラフが図 5 である。
に対して gnuplot で
書いたグラフが図 5 である。
なお、最後の 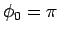 に対して注意をしておく。
この場合、
に対して注意をしておく。
この場合、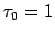 だから
だから 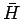 は 0 になり、
よって (27) では
は 0 になり、
よって (27) では 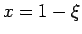 ,
, 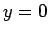 、
(28) では
、
(28) では 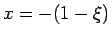 ,
, 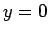 となる。
それが、円の直径になっているわけである。
となる。
それが、円の直径になっているわけである。
実際に、一般の場合でも
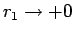 (
(
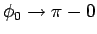 ) の
場合に
) の
場合に 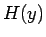 がこのような直径を表すものに収束することを示しておく。
がこのような直径を表すものに収束することを示しておく。
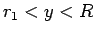 である
である 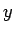 を固定し、
を固定し、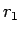 を
を
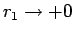 とする。このとき、(9) の被積分関数の分母は
とする。このとき、(9) の被積分関数の分母は 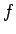 に
関して単調なので、
に
関して単調なので、
でおさえられ、よって
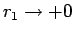 のとき
のとき
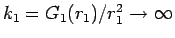 より
より
となることがわかる。すなわち、図 3 の 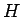 のグラフは、
のグラフは、
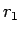 を小さくすると横軸と鉛直線
を小さくすると横軸と鉛直線 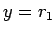 に張り付いてきて、その極限は
に張り付いてきて、その極限は
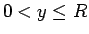 では 0、
では 0、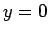 では
では 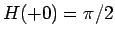 (命題 1) に
近づいていくことになる。
その結果、解は 0 と
(命題 1) に
近づいていくことになる。
その結果、解は 0 と 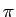 方向以外の
方向以外の 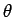 に対しては
に対しては 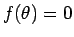 で
ある直径に近づいていくことになる。
で
ある直径に近づいていくことになる。
竹野茂治@新潟工科大学
2017年2月24日
![]() では
では ![]() とすると、
(20) より
とすると、
(20) より
![]() なので、
(19) を
なので、
(19) を
![]() に対するグラフを一緒に書く場合には、
パラメータの範囲が一定でないのは問題があるし、
関数に特異性が含まれている (
に対するグラフを一緒に書く場合には、
パラメータの範囲が一定でないのは問題があるし、
関数に特異性が含まれている (![]() で (22) の
分母が 0 になる) とそこがうまくつながらない場合があるので、
それらを修正する。
で (22) の
分母が 0 になる) とそこがうまくつながらない場合があるので、
それらを修正する。
![]() を、
を、
![]() ,
, ![]() で書き直す。
で書き直す。
![]() より
より
![]() 、
および
、
および
![]() より、
より、
![]() の方は、
(20) より
の方は、
(20) より
![]() に対して注意をしておく。
この場合、
に対して注意をしておく。
この場合、![]() だから
だから ![]() は 0 になり、
よって (27) では
は 0 になり、
よって (27) では ![]() ,
, ![]() 、
(28) では
、
(28) では ![]() ,
, ![]() となる。
それが、円の直径になっているわけである。
となる。
それが、円の直径になっているわけである。
![]() (
(
![]() ) の
場合に
) の
場合に ![]() がこのような直径を表すものに収束することを示しておく。
がこのような直径を表すものに収束することを示しておく。
![]() である
である ![]() を固定し、
を固定し、![]() を
を
![]() とする。このとき、(9) の被積分関数の分母は
とする。このとき、(9) の被積分関数の分母は ![]() に
関して単調なので、
に
関して単調なので、