3 変分法

次は (7) を最小にする関数 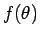$f(\theta )$ を変分法を用いて求める。

(7) の被積分関数を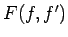とすれば、そのオイラー方程式 ([1] 参照) は

$\begin{displaymath} \frac{d}{d\theta}F_{f'} = F_f \end{displaymath}$

となる。

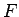は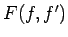

の形、すなわち陽には 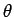$\theta$ によらない形なので、

$\begin{eqnarray*}\frac{d}{d\theta}F &=& F_ff'+F_{f'}f'' = f'\frac{d}{d\theta}F_{f'} + F_{f'}f'' = \frac{d}{d\theta}(f'F_{f'})\end{eqnarray*}$

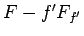となり、 $F-f'F_{f'}$ は定数となる。

今の場合は、

$\begin{eqnarray*}F-f'F_{f'} &=& \frac{\sqrt{f^2+(f')^2}}{\sqrt{G_1(f)}} -f'\f... ...t{f^2+(f')^2}} =\ \frac{f^2}{\sqrt{G_1(f)}\sqrt{f^2+(f')^2}}\end{eqnarray*}$

となるので、よって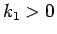

を定数として

$\begin{displaymath} G_1(f)(f^2+(f')^2)=k_1^2f^4 \end{displaymath}$

となる。変形すると、

$\begin{displaymath} (f')^2 =\frac{k_1^2f^4}{G_1(f)}-f^2 =\frac{f^2(k_1^2f^2-G_1(f))}{G_1(f)} \end{displaymath}$

なので、1 階の微分方程式

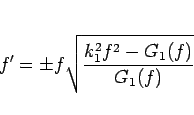$\begin{displaymath} f'=\pm f\sqrt{\frac{k_1^2f^2-G_1(f)}{G_1(f)}}\end{displaymath}$ (8)

が得られる。良く知られているように、この微分方程式の解は、変数分離法により、関数

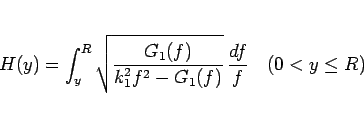$\begin{displaymath} H(y) = \int_y^R \sqrt{\frac{G_1(f)}{k_1^2f^2-G_1(f)}} \frac{df}{f} \hspace{1zw}(0< y\leq R)\end{displaymath}$ (9)

の逆関数のようなものとして得られる。

竹野茂治＠新潟工科大学
2017年2月24日