6 空間遠方に減衰している場合の減衰評価
この節では、問題 1 の空間遠方に減衰している解 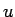 の
時間方向の減衰を考える。
の
時間方向の減衰を考える。
この場合は、
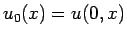 が遠方で十分速く 0 に減衰しているという仮定の元で
が遠方で十分速く 0 に減衰しているという仮定の元で 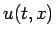 も 0 に減衰することが示される。
しかし、問題 2 の場合とは減衰する速さは異なる。
まずは簡単のため、
も 0 に減衰することが示される。
しかし、問題 2 の場合とは減衰する速さは異なる。
まずは簡単のため、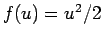 (いわゆる Burgers 方程式) とし、
(いわゆる Burgers 方程式) とし、
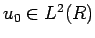 として考えてみる。
として考えてみる。
この場合は、
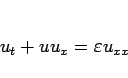
なので、
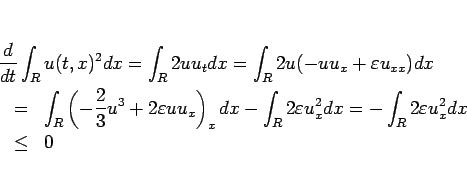
となり、よって 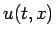 の
の 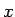 に関する
に関する 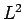 の評価
の評価
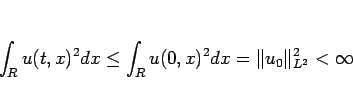 |
(21) |
が得られる。
5 節と同様に 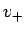 ,
, 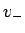 を用いれば
を用いれば
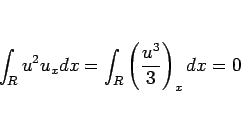
より
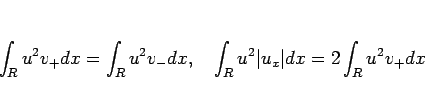 |
(22) |
となるので、
(21), (22), および定理 2 により、
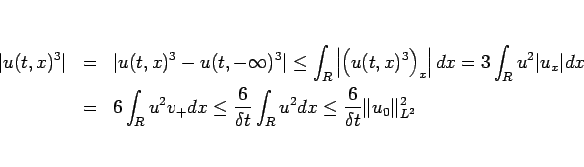
が得られる。ここから、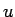 の
の 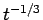 の評価
の評価
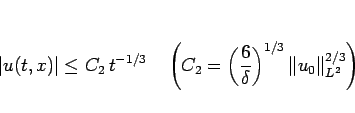 |
(23) |
が得られる。
これと同じことを、一般の 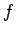 で、
で、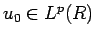 (
(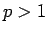 ) の場合で考えてみよう。
まず、次に注意する。
) の場合で考えてみよう。
まず、次に注意する。
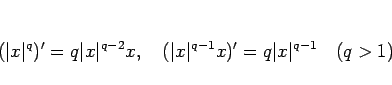 |
(24) |
これらは、
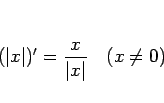
より、
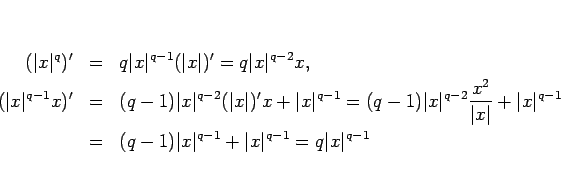
として得られる。
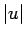 の
の 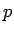 乗の積分を
乗の積分を 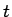 で微分すると、(24) より
で微分すると、(24) より
となるが、今
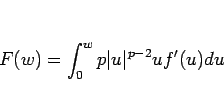 |
(26) |
とすれば、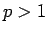 より
より 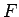 は
は 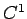 級で、よって
級で、よって
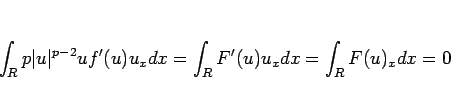 |
(27) |
となる。また、(24) より、
となるので、
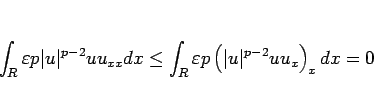 |
(29) |
となる。結局 (25), (27), (29) より
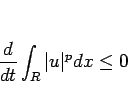
が得られるから、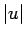 の
の 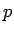 乗積分は、
乗積分は、
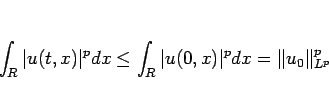 |
(30) |
と評価される。これは 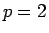 の場合の (21) に対応する。
の場合の (21) に対応する。
そして、(24) より、
となるが、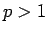 に対して (24) より、
に対して (24) より、
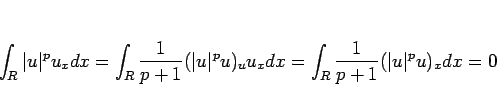
なので、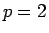 の場合と同様にして
の場合と同様にして
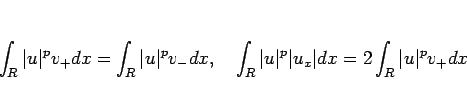
となり、よって (30) と定理 2 より、
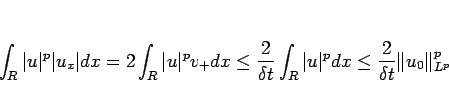
と評価できる。よって、(![[*]](crossref.gif) ) より
) より
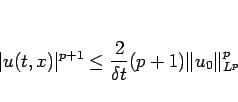
となり、結局 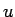 の
の 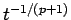 の評価
の評価
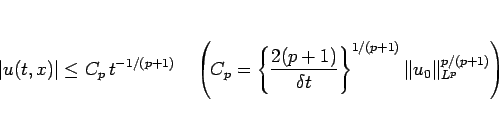 |
(32) |
が得られる。
また、特に 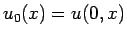 がコンパクト台を持つ関数の場合は、
すべての
がコンパクト台を持つ関数の場合は、
すべての 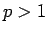 に対し
に対し 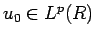 となるので、
(32) で
となるので、
(32) で
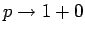 とすれば、
とすれば、
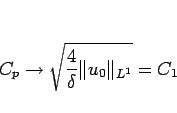
となり、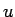 の
の 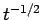 の評価
の評価
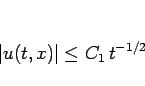
が得られる。
定理 4
問題 1 の場合、
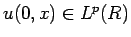 (
(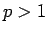 ) のときは、
(2) の解
) のときは、
(2) の解 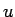 は
は 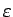 に一様に
次の減衰評価を満たす。
に一様に
次の減衰評価を満たす。
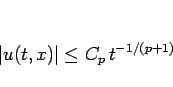 |
(33) |
さらに 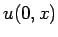 がコンパクト台を持つ場合は
がコンパクト台を持つ場合は
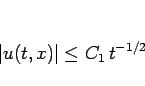 |
(34) |
が成り立つ (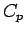 は
は 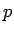 ,
, 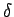 ,
, 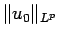 による定数)。
による定数)。
初期値がコンパクト台を持つ場合の 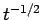 という評価は、
コンパクトな台を持つ
という評価は、
コンパクトな台を持つ 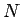 型波の漸近挙動に対応し、
よって
型波の漸近挙動に対応し、
よって 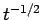 より強い評価を期待することはできない (詳細は、例えば [1] 参照)。
より強い評価を期待することはできない (詳細は、例えば [1] 参照)。
なお、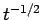 の評価を得るために (25) を直接
の評価を得るために (25) を直接 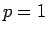 としようとすると、
としようとすると、
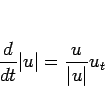
は 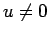 でしか成り立たないため、
でしか成り立たないため、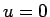 での例外的な議論が入って難しくなる。
さらに (26) の
での例外的な議論が入って難しくなる。
さらに (26) の  も
も 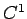 ではなくなるし、
(28) も
ではなくなるし、
(28) も 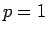 ではそのままは成立しない。
つまり
ではそのままは成立しない。
つまり 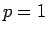 では上のような議論が直接は使えないので、
ここでは
では上のような議論が直接は使えないので、
ここでは
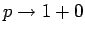 として考えた。
しかし
として考えた。
しかし 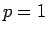 でも似たような考察が行えないわけではない。
それについては付録として 8 節に記すこととする。
でも似たような考察が行えないわけではない。
それについては付録として 8 節に記すこととする。
また、この節では、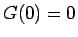 なる
なる 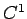 級の関数
級の関数 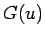 に対して、
に対して、
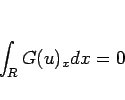
なる論法を何回か用いた。
これが成り立つためには、もちろん 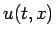 にそれなりの速さでの
にそれなりの速さでの 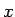 の遠方での減衰性や微分の可積分性などが必要になる (詳しくは [3] 参照) が、
我々の問題では元々考えている
の遠方での減衰性や微分の可積分性などが必要になる (詳しくは [3] 参照) が、
我々の問題では元々考えている 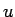 は (1) に対する近似解なので、
必要ならば初期値も
は (1) に対する近似解なので、
必要ならば初期値も 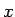 の遠方では十分早く減衰するもので近似しておくことができ、
それほど問題とはならない (多分)。
の遠方では十分早く減衰するもので近似しておくことができ、
それほど問題とはならない (多分)。
竹野茂治@新潟工科大学
2009年1月25日
![]() が遠方で十分速く 0 に減衰しているという仮定の元で
が遠方で十分速く 0 に減衰しているという仮定の元で ![]() も 0 に減衰することが示される。
しかし、問題 2 の場合とは減衰する速さは異なる。
まずは簡単のため、
も 0 に減衰することが示される。
しかし、問題 2 の場合とは減衰する速さは異なる。
まずは簡単のため、![]() (いわゆる Burgers 方程式) とし、
(いわゆる Burgers 方程式) とし、
![]() として考えてみる。
として考えてみる。
![]() で、
で、![]() (
(![]() ) の場合で考えてみよう。
まず、次に注意する。
) の場合で考えてみよう。
まず、次に注意する。
![]() の
の ![]() 乗の積分を
乗の積分を ![]() で微分すると、(24) より
で微分すると、(24) より
![[*]](crossref.gif) ) より
) より
![]() がコンパクト台を持つ関数の場合は、
すべての
がコンパクト台を持つ関数の場合は、
すべての ![]() に対し
に対し ![]() となるので、
(32) で
となるので、
(32) で
![]() とすれば、
とすれば、
![]() (
(![]() ) のときは、
(2) の解
) のときは、
(2) の解 ![]() は
は ![]() に一様に
次の減衰評価を満たす。
に一様に
次の減衰評価を満たす。
![]() という評価は、
コンパクトな台を持つ
という評価は、
コンパクトな台を持つ ![]() 型波の漸近挙動に対応し、
よって
型波の漸近挙動に対応し、
よって ![]() より強い評価を期待することはできない (詳細は、例えば [1] 参照)。
より強い評価を期待することはできない (詳細は、例えば [1] 参照)。
![]() の評価を得るために (25) を直接
の評価を得るために (25) を直接 ![]() としようとすると、
としようとすると、
![]() なる
なる ![]() 級の関数
級の関数 ![]() に対して、
に対して、