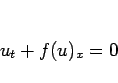1 はじめに

本稿は、保存則方程式

$$u_t+f(u)_x=0$$ (1)

の解の減衰について考える。 ここで $u=u(t,x)$ は、一般には $N$ 次元の値を取る、 $t>0$, $x\in R$ の 2 変数関数で、 $f(u)$ は $u$ に関して $C^2$ であるとする。

方程式 (1) は、 解が不連続性を持ちうる (衝撃波として知られている) ので、 解の存在を示すには、何らかの近似解、例えば人工粘性方程式

$$u_t+f(u)_x=\varepsilon u_{xx}$$ (2)

($\varepsilon>0$) の解などを構成し、 その極限 ( $\varepsilon\rightarrow +0$) として (1) の解 (弱解) を得るのが普通であり、 そのような方法も、 Glimm 差分や波面追跡法 (front tracking method) など、何通りか知られている。

減衰性のような解の性質を、 直接 (1) を扱う代わりに (2) の解の性質の極限として得るには、 $\varepsilon$ によらない一様な性質が必要となる。 解の減衰等の研究は、(2) よりもむしろ Glimm 差分や波面追跡法などによる研究の方が進んでいるが、 ここでは、補償コンパクト性理論 (compensated compactness theory) で使用される (2) による近似解について考察する。

なお本稿は、議論のアウトラインに関するノートであるため、 厳密さを欠いたような説明や、 必要な条件を精密に表現しないような説明も含まれるので注意してもらいたい。