8 可積分な初期値について
この節では、付録として、6 節の最後に述べた、
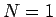 で初期値が可積分な場合の一様な評価
で初期値が可積分な場合の一様な評価 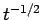 を、
を、
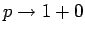 の極限としてではなく直接得るための計算を考えてみる。
の極限としてではなく直接得るための計算を考えてみる。
そこで述べたように、この場合は
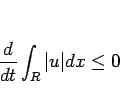
を示してそれを積分する、というわけにはいかないので、
最初から微分を積分の中に入れた形で考える。ただし、
絶対値のついた関数の微分を考えるために、
右からの微分係数 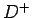 を用いる。
を用いる。
補題 5
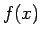 が
が 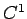 級のとき、
級のとき、
![\begin{displaymath}
D^{+}\vert f(x)\vert
=\lim_{h\rightarrow +0}\frac{\vert f(...
...q 0),\ [1zh]
\vert f'(x)\vert & (f(x)=0)
\end{array}\right. \end{displaymath}](img192.gif) |
(36) |
証明
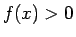 ,
, 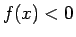 の場合は、
それぞれ
の場合は、
それぞれ 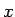 の近くでも
の近くでも 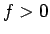 ,
, 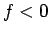 であるから (36) は明らか。
であるから (36) は明らか。
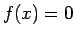 の場合は、
の場合は、
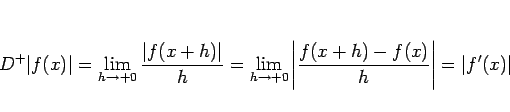
となる。
補題 6
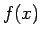 が
が
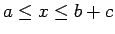 (
(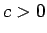 ) で
) で 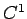 級のとき、
級のとき、
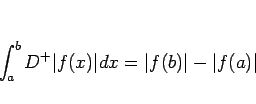
証明
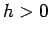 ,
, 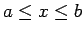 に対して
に対して
![\begin{displaymath}
\left\vert\frac{\vert f(x+h)\vert-\vert f(x)\vert}{h}\right...
...x)}{h}\right\vert
\leq\max_{[a,b+c]}\vert f'(x)\vert <\infty
\end{displaymath}](img204.gif)
なので、Lebesgue 収束定理により
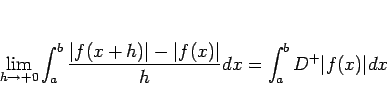
となる。一方、
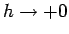 のとき、
のとき、
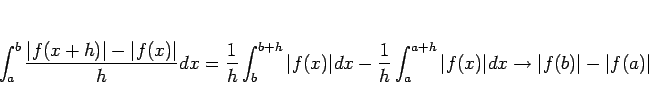
となる。
この補題 6 によって、任意の 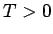 に対し、
に対し、
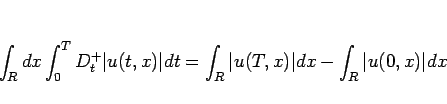 |
(37) |
が成り立つ。ここで、
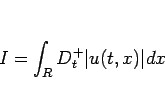
の積分範囲を、
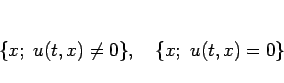
の 2 つに分けると、補題 5 より、
となる。
まず、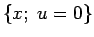 上の積分であるが、
これは次の補題 7 により 0 となることがわかる。
上の積分であるが、
これは次の補題 7 により 0 となることがわかる。
補題 7
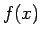 が
が 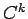 級 (
級 (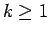 ) のとき、
) のとき、
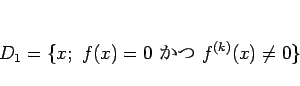
は高々加算集合。
この補題 7 は、
次の補題 8 により得られる。
補題 8
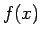 が
が 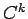 級 (
級 (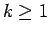 ) のとき、任意の
) のとき、任意の 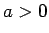 に対して、
に対して、
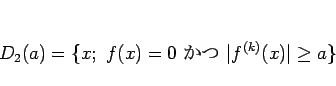
は集積点を持たない。
この補題 8 が言えれば、
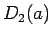 は離散的なので高々可算集合となり、よって
は離散的なので高々可算集合となり、よって
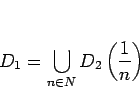
も高々可算集合であることが言え、
補題 7 が成り立つことになる。
この補題 8 は、以下のようにして示される。
今、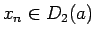 (
(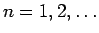 ) がすべて異なる点列で、
) がすべて異なる点列で、
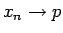 であるとする。
このとき、
であるとする。
このとき、
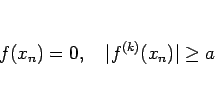
なので、その極限においても
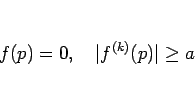
となり、よって 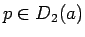 となる。
となる。
ところで、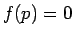 とロピタルの定理により、
とロピタルの定理により、
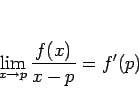
となるが、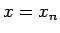 に対しては
に対しては
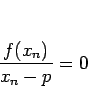
なので、よって 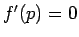 となる。
そしてこれにより、再びロピタルの定理により、
となる。
そしてこれにより、再びロピタルの定理により、
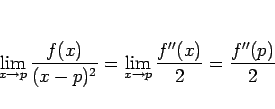
となるが、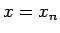 においてはやはり
においてはやはり
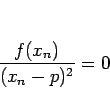
なので、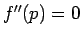 となる。
これを繰り返して結局
となる。
これを繰り返して結局 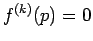 が得られるが、
これは
が得られるが、
これは
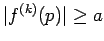 に矛盾する。
よって
に矛盾する。
よって 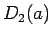 は集積点を持たない。
は集積点を持たない。
結局 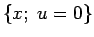 上の積分は 0 となるので、
(38) より
上の積分は 0 となるので、
(38) より
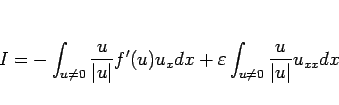 |
(39) |
となる。この最初の積分は、
と変形できる。ここで 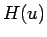 は、
は、
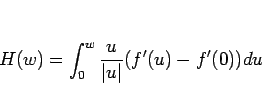
で定義される 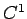 級の関数である。
級の関数である。
今、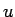 は
は 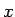 に関して連続なので
に関して連続なので
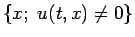 は
開集合であるが、その連結成分は開区間であり、
それらは高々可算個で共通部分を持たず、
は
開集合であるが、その連結成分は開区間であり、
それらは高々可算個で共通部分を持たず、
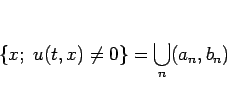
と書ける。各区間 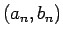 では
では 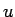 は正、または負のいずれかであり、
は正、または負のいずれかであり、
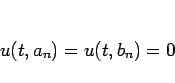 |
(41) |
となる。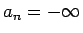 , あるいは
, あるいは 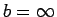 の場合も
の場合も 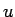 は遠方で 0 に収束するから、
その場合も (41) は成り立つと見ることができる。
よって、
は遠方で 0 に収束するから、
その場合も (41) は成り立つと見ることができる。
よって、
![\begin{displaymath}
\int_{u\neq 0}H(u)_xdx
=\sum_n\int_{a_n}^{b_n}H(u)_xdx
=\sum_n\left[H(u)\right]_{a_n}^{b_n}
=0
\end{displaymath}](img250.gif)
となる。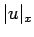 の積分の方も同様に 0 となる (
の積分の方も同様に 0 となる (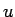 ,
, 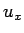 に適当な減衰性があるという仮定の元)。
よって、
に適当な減衰性があるという仮定の元)。
よって、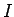 は
は
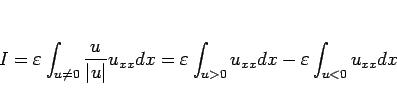
のみが残ることとなるが、この積分は (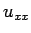 も可積分であるとし、遠方での減衰性を仮定すれば)、
上と同様に各開区間の積分に分けることができて、
も可積分であるとし、遠方での減衰性を仮定すれば)、
上と同様に各開区間の積分に分けることができて、
と変形できる。
ここで 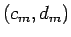 上では
上では 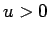 、
、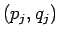 上では
上では 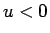 で、
で、
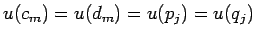 であるから、
であるから、
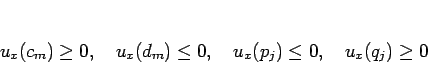
となる。よって、
![\begin{displaymath}
\left[u_x\right]_{c_m}^{d_m}\leq 0,\hspace{1zw}
\left[u_x\right]_{p_j}^{q_j}\geq 0\end{displaymath}](img263.gif) |
(43) |
となるので、
よって (42), (43) より 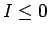 が言え、
結局 (37) と Fubini の定理により、任意の
が言え、
結局 (37) と Fubini の定理により、任意の 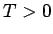 に対して
に対して
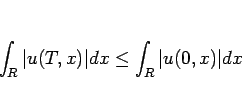
が言えることになる。
これが言えてしまえば後は前と同じで、
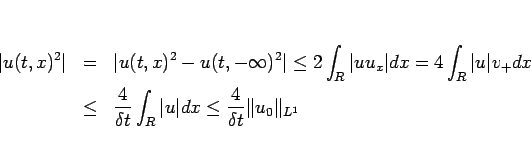
となり、(34) が得られることになる。
ただしこちらの場合は、
それなりに 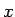 の遠方に関する減衰性や可積分性は必要とするものの、
の遠方に関する減衰性や可積分性は必要とするものの、
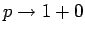 の極限を用いないので、
初期値がコンパクト台を持つ必要はない。
の極限を用いないので、
初期値がコンパクト台を持つ必要はない。
竹野茂治@新潟工科大学
2009年1月25日
![]() が
が ![]() 級のとき、
級のとき、
![]() ,
, ![]() の場合は、
それぞれ
の場合は、
それぞれ ![]() の近くでも
の近くでも ![]() ,
, ![]() であるから (36) は明らか。
であるから (36) は明らか。
![]() の場合は、
の場合は、
![]() が
が
![]() (
(![]() ) で
) で ![]() 級のとき、
級のとき、
![]() ,
, ![]() に対して
に対して
![]() に対し、
に対し、
![]() が
が ![]() 級 (
級 (![]() ) のとき、
) のとき、
![]() が
が ![]() 級 (
級 (![]() ) のとき、任意の
) のとき、任意の ![]() に対して、
に対して、
![]() は離散的なので高々可算集合となり、よって
は離散的なので高々可算集合となり、よって
![]() (
(![]() ) がすべて異なる点列で、
) がすべて異なる点列で、
![]() であるとする。
このとき、
であるとする。
このとき、
![]() とロピタルの定理により、
とロピタルの定理により、
![]() 上の積分は 0 となるので、
(38) より
上の積分は 0 となるので、
(38) より
![]() は
は ![]() に関して連続なので
に関して連続なので
![]() は
開集合であるが、その連結成分は開区間であり、
それらは高々可算個で共通部分を持たず、
は
開集合であるが、その連結成分は開区間であり、
それらは高々可算個で共通部分を持たず、
![]() の遠方に関する減衰性や可積分性は必要とするものの、
の遠方に関する減衰性や可積分性は必要とするものの、
![]() の極限を用いないので、
初期値がコンパクト台を持つ必要はない。
の極限を用いないので、
初期値がコンパクト台を持つ必要はない。