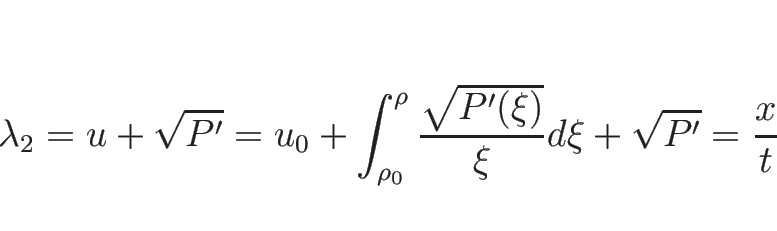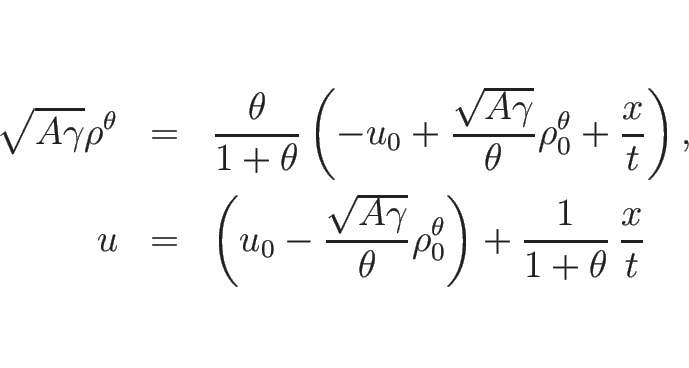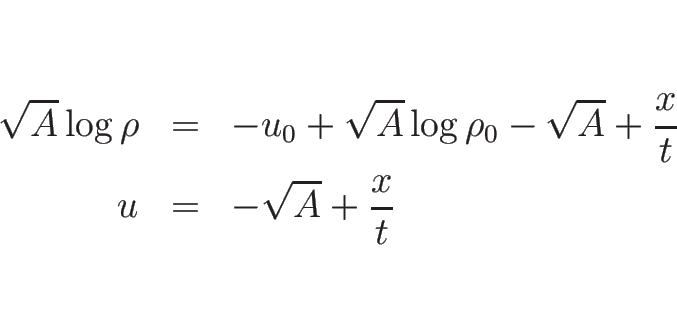3.7 バロトロピックのオイラー座標系の場合の例
2.5 節の最後に書いたように、
オイラー座標系での保存則方程式の圧力を 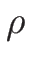 のみの関数
のみの関数
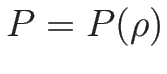 とみて、質量保存則 (2.10) と
運動量保存則 (2.15) のみで
閉じた系と考えることも多い。ここでは、その場合を考えてみる。
この場合は通常等エントロピー流:
とみて、質量保存則 (2.10) と
運動量保存則 (2.15) のみで
閉じた系と考えることも多い。ここでは、その場合を考えてみる。
この場合は通常等エントロピー流:
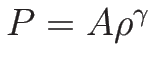 (
(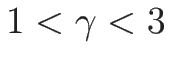 )
や等温流:
)
や等温流: 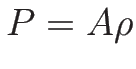 を想定していることが多く、
を想定していることが多く、
を仮定する場合が多い。
まず、方程式を
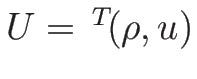 の方程式に書き直すと、
3.5 節の計算により、
の方程式に書き直すと、
3.5 節の計算により、
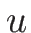 に関する方程式がこの場合は
に関する方程式がこの場合は
となるので、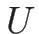 に関して
に関して
と書ける。
より、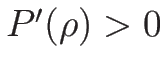 の仮定の元で、固有値は
の仮定の元で、固有値は
で、固有ベクトルは
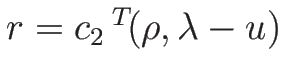 より、
より、
となり、
で、
となるので、
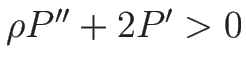 ならば 1-特性方向も 2-特性方向も
真性非線形となる。
ならば 1-特性方向も 2-特性方向も
真性非線形となる。
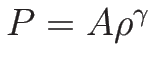 (
(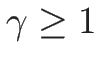 ) の場合であれば、
) の場合であれば、
なので確かに正となる。
リーマン不変量は、
より、
を解いて、
となるので、
となるので、この左辺が 1-リーマン不変量となる。
同様に、2-リーマン不変量は、
となる。
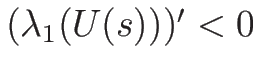 なのでパラメータ
なのでパラメータ 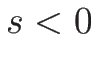 となり、
よって 1-膨張波曲線
となり、
よって 1-膨張波曲線 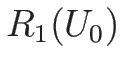 は、
は、
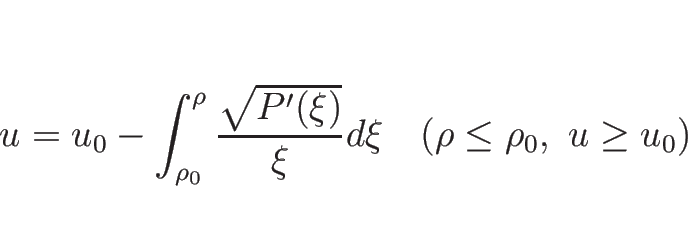 |
(3.45) |
2-膨張波曲線 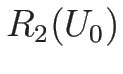 は
は
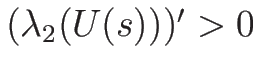 より
より 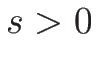 なので
なので
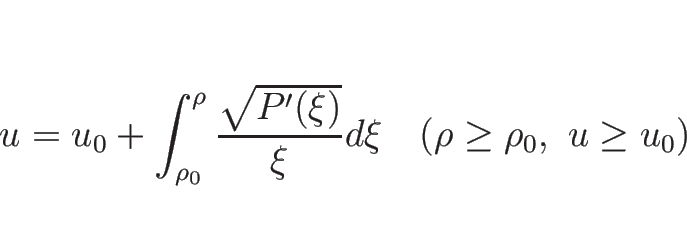 |
(3.46) |
となる。
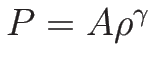 (
(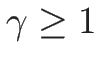 ) の場合で言えば、
) の場合で言えば、
なので、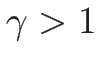 と
と 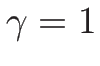 とで
とで
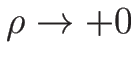 のときの挙動が異なり、
のときの挙動が異なり、
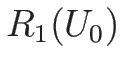 は、
は、
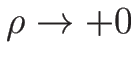 のときに
のときに
となる。つまり、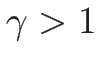 のときは
のときは 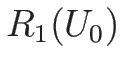 は
は
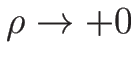 のときに有限の
のときに有限の 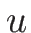 のところで
のところで 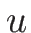 軸に当たって止まるが、
軸に当たって止まるが、
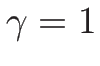 のときには
のときには 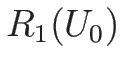 は
は 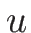 軸を漸近線として無限に伸びる。
軸を漸近線として無限に伸びる。
なおこの違いは、リーマン問題が真空状態 (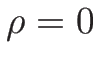 ) を解として
含むかどうかに関係する。
) を解として
含むかどうかに関係する。
また、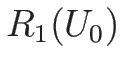 の場合は (3.26) により、
の場合は (3.26) により、
であるから、
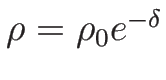 とすれば
とすれば 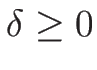 で、
で、
となり、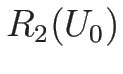 の場合は (3.27) により、
の場合は (3.27) により、
であるから、
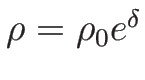 とすれば
とすれば  で、
で、
となる。
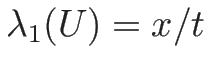 に (3.26) を代入すると、
に (3.26) を代入すると、
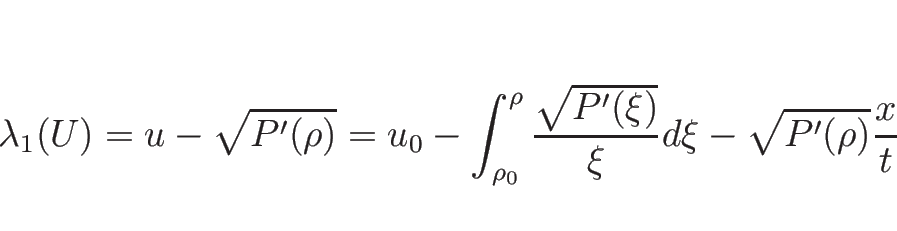 |
(3.47) |
となるので、これを 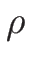 について解けば、
そしてそれを (3.26) に代入すれば
について解けば、
そしてそれを (3.26) に代入すれば
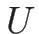 を
を 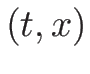 の式で表される。
の式で表される。
例えば
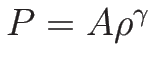 (
(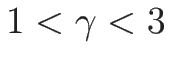 ) の場合、
(3.28) は
) の場合、
(3.28) は
となるので、
のようになる。
また、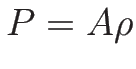 のときは (3.28) は
のときは (3.28) は
より、この場合は
となる。
同様に、 は、
は、
となるから、
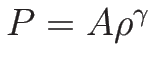 (
(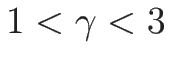 ) の場合は、
) の場合は、
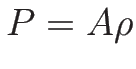 の場合は、
の場合は、
となる。
竹野茂治@新潟工科大学
2018-08-01
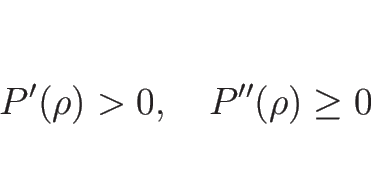
![]() の方程式に書き直すと、
3.5 節の計算により、
の方程式に書き直すと、
3.5 節の計算により、
![]() に関する方程式がこの場合は
に関する方程式がこの場合は
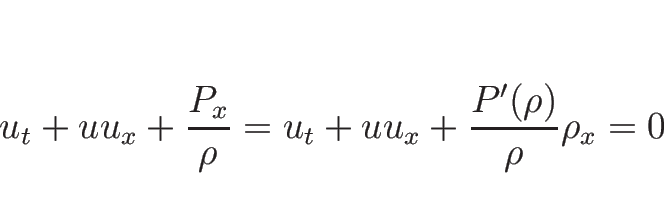
![\begin{displaymath}
\left[\begin{array}{c}\rho\\ u\end{array}\right]_t
+\left[\b...
...}\right]
\left[\begin{array}{c}\rho\\ u\end{array}\right]_x
=0
\end{displaymath}](img439.png)
![\begin{displaymath}
\left\vert\begin{array}{cc}
\lambda-u & -\rho \\ [.5zh]
\d...
...{\rho} & \lambda-u
\end{array}\right\vert=(\lambda-u)-P'(\rho)
\end{displaymath}](img440.png)
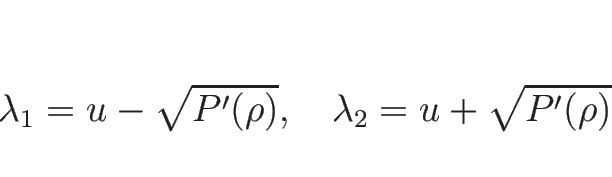
![\begin{displaymath}
r_1=\left[\begin{array}{c}-\rho\\ \sqrt{P'}\end{array}\right...
...w}r_2=\left[\begin{array}{c}\rho\\ \sqrt{P'}\end{array}\right]
\end{displaymath}](img444.png)
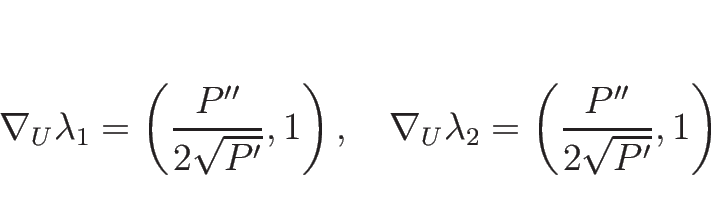
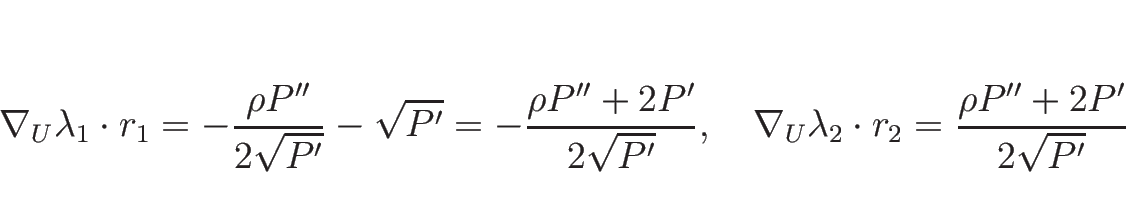
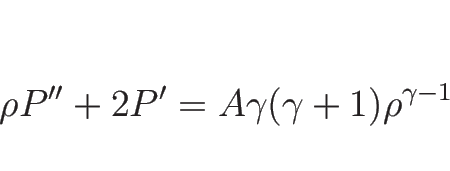
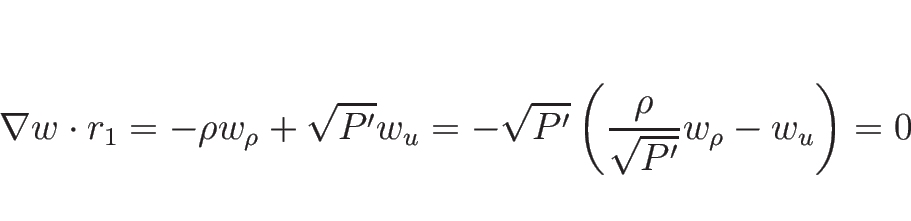
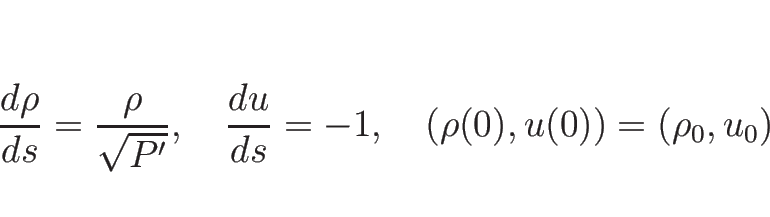
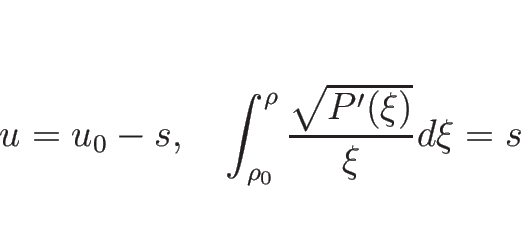
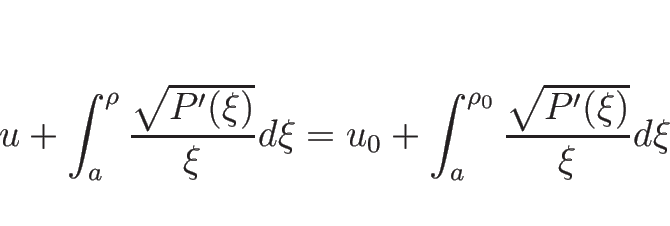
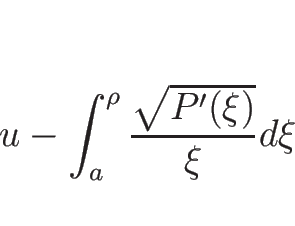
![]() なのでパラメータ
なのでパラメータ ![]() となり、
よって 1-膨張波曲線
となり、
よって 1-膨張波曲線 ![]() は、
は、
![]() (
(![]() ) の場合で言えば、
) の場合で言えば、
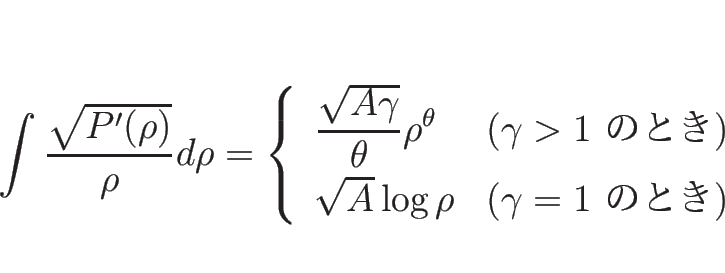
![\begin{displaymath}
u\rightarrow
\left\{\begin{array}{ll}
\displaystyle u_0+\fr...
...[.5zh]
+\infty & (\mbox{$\gamma=1$\ のとき})\end{array}\right.\end{displaymath}](img464.png)
![]() ) を解として
含むかどうかに関係する。
) を解として
含むかどうかに関係する。
![]() の場合は (3.26) により、
の場合は (3.26) により、
![\begin{displaymath}
\frac{d U}{d \rho}
=\frac{d}{d \rho}\left[\begin{array}{c}\r...
...c}1\\ -\sqrt{P'}/\rho\end{array}\right]
=-\frac{1}{\rho}r_1(U)
\end{displaymath}](img466.png)
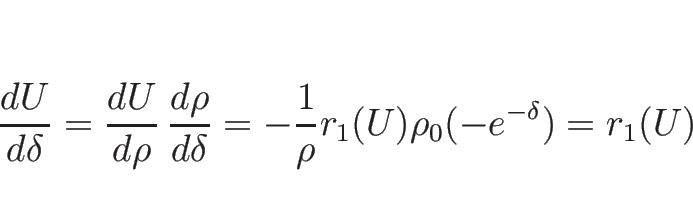
![\begin{displaymath}
\frac{d U}{d \rho}
=\frac{d}{d \rho}\left[\begin{array}{c}\r...
...}{c}1\\ \sqrt{P'}/\rho\end{array}\right]
=\frac{1}{\rho}r_2(U)
\end{displaymath}](img469.png)
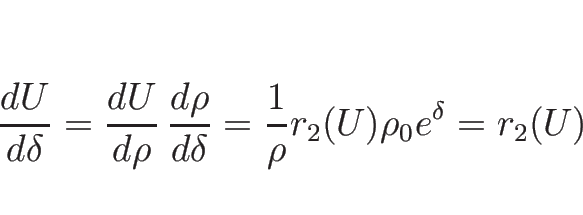
![]() に (3.26) を代入すると、
に (3.26) を代入すると、
![]() (
(![]() ) の場合、
(3.28) は
) の場合、
(3.28) は
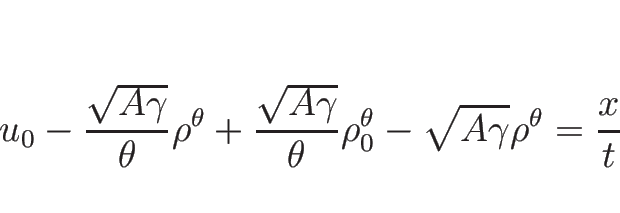
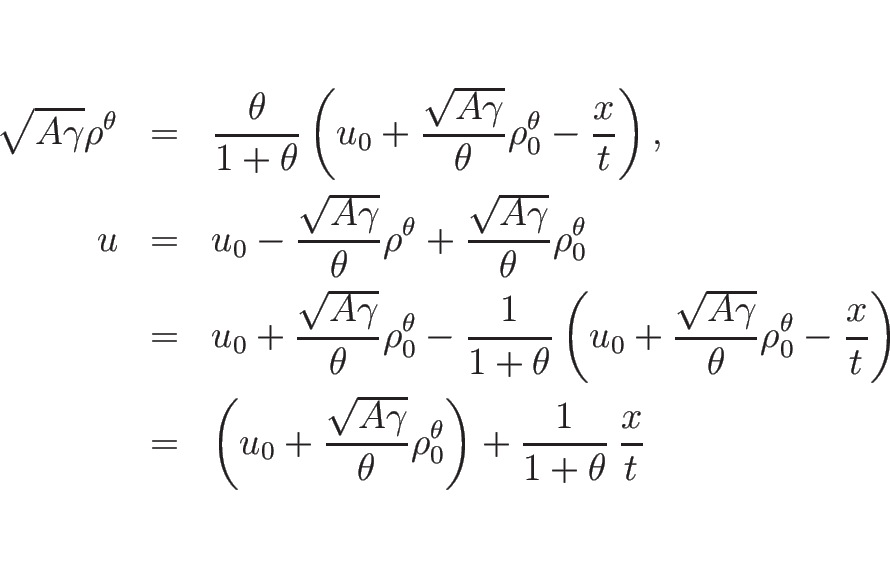
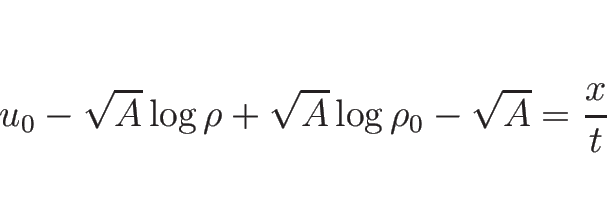
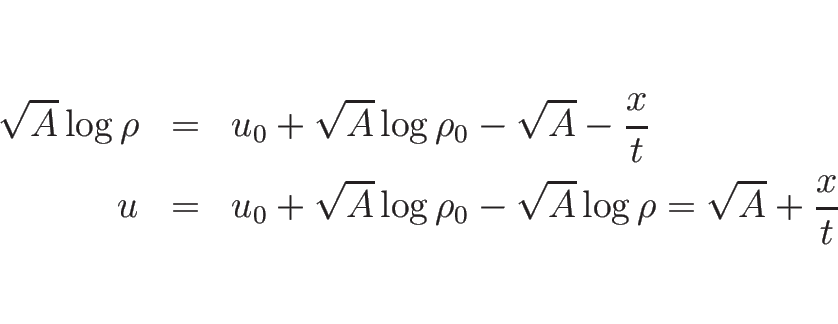
![]() は、
は、