2.2 節で
質量に対して ![]() ,
, ![]() ,
, ![]() ,
, ![]() のように書いたものを、
質量を運動量で置き換えたものを
のように書いたものを、
質量を運動量で置き換えたものを ![]() ,
, ![]() ,
, ![]() ,
, ![]() のように書くことにする。それを局所化したものを、
ここでは
のように書くことにする。それを局所化したものを、
ここでは ![]() ,
, ![]() と書くことにする。すなわち、
と書くことにする。すなわち、
運動量は質量と速度の積なので、
![]() のとき
のとき
![\begin{displaymath}
M^2_{[x,x+\Delta x]}(t)\approx M^1_{[x,x+\Delta x]}(t)u(t,x)
\end{displaymath}](img114.png)
2.3 節の (2.6) の関係式は、
そのまま ![]() ,
, ![]() を
を ![]() ,
, ![]() に
置き換えたものが成立し、その後の議論もそのまま成立する。
よって、この場合 (2.7) に変わって
に
置き換えたものが成立し、その後の議論もそのまま成立する。
よって、この場合 (2.7) に変わって
![]() ,
, ![]() での運動量の変化を考えると、
それは運動量の流入と流出だけではなく力積も追加されるので、
での運動量の変化を考えると、
それは運動量の流入と流出だけではなく力積も追加されるので、
![\begin{displaymath}
M^2_{[a,b]}(d)-M^2_{[a,b]}(c)=N^2_{[c,d]}(a)-N^2_{[c,d]}(b)+K\end{displaymath}](img119.png)
もし、この気体には力としては圧力しか働いていない (つまり外力はない)
とすると、
![]() を時刻
を時刻 ![]() のときに
のときに ![]() での断面全体で左右に向く気体の圧力とすれば、
圧力はどの方向にも等しく働くスカラー量であるから、
での断面全体で左右に向く気体の圧力とすれば、
圧力はどの方向にも等しく働くスカラー量であるから、
![]() の内部では圧力による力積は左右分が打ち消されるので 0 であり、
よって境界で働く圧力のみがこの内部の運動量の増減に関係する。
力積は、力と時間の積で得られるので、結局
の内部では圧力による力積は左右分が打ち消されるので 0 であり、
よって境界で働く圧力のみがこの内部の運動量の増減に関係する。
力積は、力と時間の積で得られるので、結局 ![]() は
は
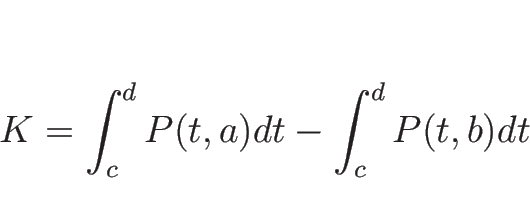
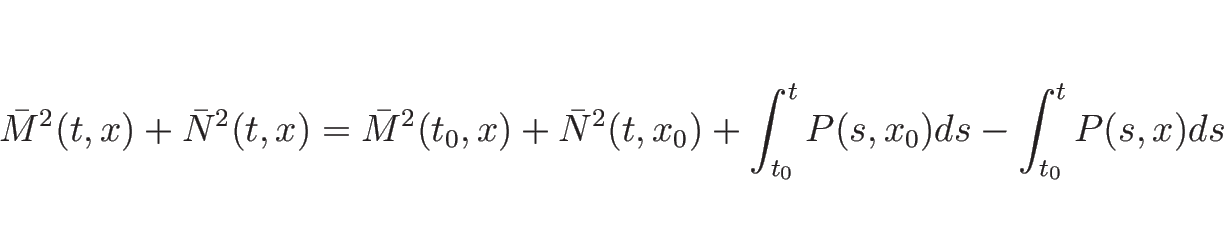
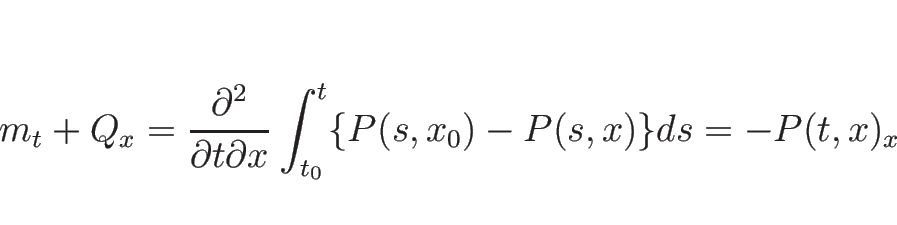
エネルギー保存則も同様に考えることができ、
エネルギー密度を ![]() とすれば、
運動量の場合に境界からの追加が力積であった部分が、
エネルギーの場合は境界から仕事量として
とすれば、
運動量の場合に境界からの追加が力積であった部分が、
エネルギーの場合は境界から仕事量として
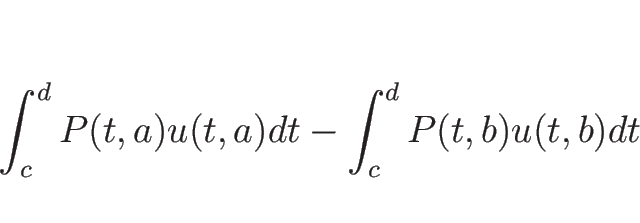
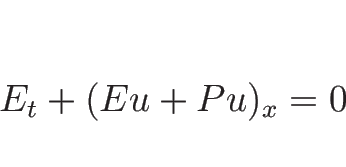
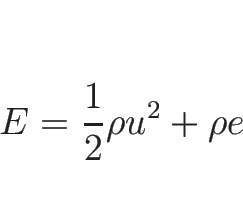
この (2.10), (2.15), (2.16) の 3 本の連立微分方程式が、
1 次元の理想気体の基礎的な保存則方程式系であり、
この場合未知関数は、![]() や
や ![]() などと考えて
考察することになる。
などと考えて
考察することになる。
また、圧力 ![]() が密度
が密度 ![]() のみによって決定するバロトロピー流
(
のみによって決定するバロトロピー流
(![]() 、例えば等エントロピー流:
、例えば等エントロピー流:
![]() ,
等温流:
,
等温流: ![]() など) であるという仮定を置いて、
エネルギー保存則 (2.16) を除いた
(2.10), (2.15) の 2 本
だけで考察することもよく行われる。この場合は、
など) であるという仮定を置いて、
エネルギー保存則 (2.16) を除いた
(2.10), (2.15) の 2 本
だけで考察することもよく行われる。この場合は、
![]() や
や ![]() を未知関数と考える。
を未知関数と考える。
竹野茂治@新潟工科大学