2.4 質量保存則
次に、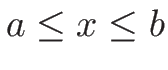 での、時刻
での、時刻 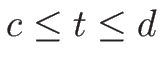 の間の質量変化
の間の質量変化
を考える。この質量の増加分は、
この間に 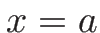 に左から流入した質量
に左から流入した質量
![$N^1_{[c,d]}(a)$](img82.png) と、
と、
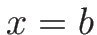 から右へ流出した質量
から右へ流出した質量
![$N^1_{[c,d]}(b)$](img93.png) との差に等しいので、
との差に等しいので、
![\begin{displaymath}
M^1_{[a,b]}(d)-M^1_{[a,b]}(c)=N^1_{[c,d]}(a)-N^1_{[c,d]}(b)\end{displaymath}](img94.png) |
(2.8) |
が成り立つ。
これを 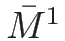 ,
, 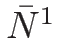 で書き下すと、
で書き下すと、
となる。
これは、任意の 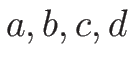 について成り立つので、
について成り立つので、
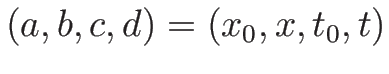 とすれば、
定義より
とすれば、
定義より
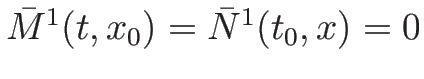 なので、
なので、
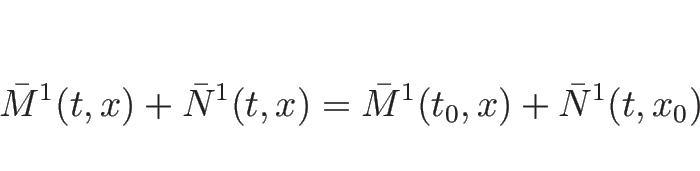 |
(2.9) |
が得られる。
これを 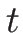 と
と 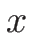 で微分すれば、
右辺は
で微分すれば、
右辺は 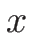 のみの関数と
のみの関数と 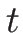 のみの関数なので 0 となり、
また (2.3), (2.7) より
のみの関数なので 0 となり、
また (2.3), (2.7) より
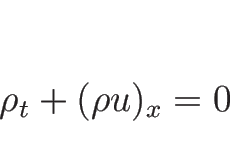 |
(2.10) |
が得られる。これは質量保存を示す微分方程式で、連続の方程式
と呼ばれる。
なお、(2.9) は
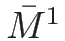 ,
, 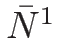 に対する質量保存則を意味する。
に対する質量保存則を意味する。
竹野茂治@新潟工科大学
2018-08-01
![\begin{displaymath}
M^1_{[a,b]}(d)-M^1_{[a,b]}(c)
\end{displaymath}](img92.png)
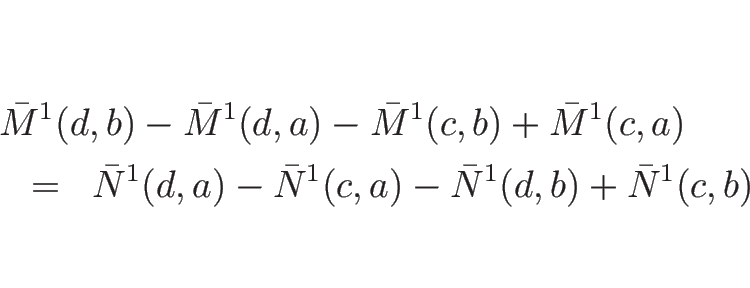
![]() と
と ![]() で微分すれば、
右辺は
で微分すれば、
右辺は ![]() のみの関数と
のみの関数と ![]() のみの関数なので 0 となり、
また (2.3), (2.7) より
のみの関数なので 0 となり、
また (2.3), (2.7) より
![]() ,
, ![]() に対する質量保存則を意味する。
に対する質量保存則を意味する。