
 の極限を考える代わりに,
の極限を考える代わりに,  倍の積分の極限 (37) を考えることがその主な部分である.
倍の積分の極限 (37) を考えることがその主な部分である.
この改良によって, DiPerna[3] の結果よりも良いことが示された
わけではないが, 証明が多少シンプルになり, 証明に使われるエントロピーに
対する制約が多少緩められ,  ,
,
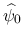 は (16) と (32) の条件, および (34) の
は (16) と (32) の条件, および (34) の 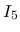 が 0 でないものを
取ればよいこと, 例えば (41) のような
簡単な関数で構成できることがわかる.
が 0 でないものを
取ればよいこと, 例えば (41) のような
簡単な関数で構成できることがわかる.
一方この方法を, 一般の
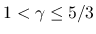 に対する Ding-Chen-Luo[2] の結果に適用すると, 彼らの膨大な計算を簡略化で
きる可能性があるだけでなく,
に対する Ding-Chen-Luo[2] の結果に適用すると, 彼らの膨大な計算を簡略化で
きる可能性があるだけでなく,  に関する条件を
に関する条件を
 か
か 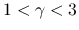 まで広げられる可能性もある. それについても今後紹介したいと思うが, 存在定理はすでに一般の
まで広げられる可能性もある. それについても今後紹介したいと思うが, 存在定理はすでに一般の 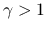 に
対して示されているので, その改良により特に新しい結果が得られるわけではない.
しかし, さらにより一般の
に
対して示されているので, その改良により特に新しい結果が得られるわけではない.
しかし, さらにより一般の  に結果を拡張する場合には
このような簡略化の考察が解決につながる可能性はあるし, この分野の学習を多少容易にすることにはなるので, 意味のないことではないと考える.
に結果を拡張する場合には
このような簡略化の考察が解決につながる可能性はあるし, この分野の学習を多少容易にすることにはなるので, 意味のないことではないと考える.
竹野茂治@新潟工科大学