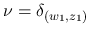
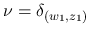 であることを示す.
であることを示す.
命題 2 より,
 は 0 以上で,
は 0 以上で,
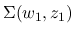 上で 0 になるのは
上で 0 になるのは 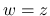 か, または
か, または  で
で
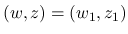 の場合のみである.
の場合のみである.
よって, (39) より, 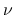 の台はそこに含まれる
ことになり, 台 が
の台はそこに含まれる
ことになり, 台 が 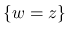 に含まれる非負の測度
に含まれる非負の測度 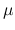 により
により
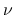 の台は点
の台は点 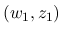 を含むから
を含むから 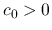 である.
である.
一方, Tartar 方程式より

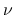 の被積分関数はいずれも
の被積分関数はいずれも 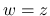 で 0 で, よって (42) より,
で 0 で, よって (42) より, 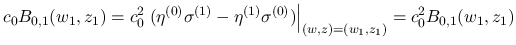
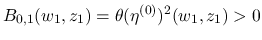 より
より
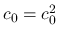 となるので
となるので 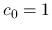 となる.
となる.
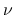 も
も
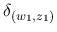 も全測度 1 なので, よって
も全測度 1 なので, よって  となり, これで
となり, これで
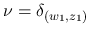 が得られる.
が得られる.
なお, 本節の議論は標準的な手法[9] であり, 改良点は特にない.
竹野茂治@新潟工科大学