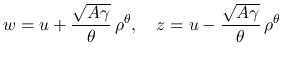 (8)
(8)
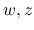 を「Riemann 不変量」と呼ぶ.
ここで
を「Riemann 不変量」と呼ぶ.
ここで 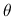 は
は
 の定数で,
の定数で, 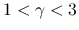 では
では 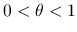 である.
である.
 という組は,
という組は, 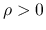 の範囲では
の範囲では 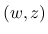 という組に 1 対 1 に対応し,
という組に 1 対 1 に対応し,
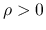 な解に対しては,
な解に対しては,  で考えることと
で考えることと 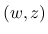 で考えることは同等となる.
弱エントロピー対
で考えることは同等となる.
弱エントロピー対 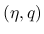 や Young 測度
や Young 測度
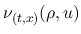 も,
も, 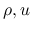 の関数,
の関数, 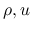 の測度と考える代わりに
の測度と考える代わりに 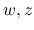 の関数,
の関数, 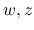 の測度, と考えることもできる.
の測度, と考えることもできる.
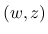 で考えると方程式 (3) も対角化され, 色々見通しが良くなり, 本稿でもほぼ
で考えると方程式 (3) も対角化され, 色々見通しが良くなり, 本稿でもほぼ 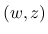 で考察する.
で考察する.
補償コンパクト性理論で用いられる (3) の
近似解は, 一様有界性を持つ人工粘性近似や Lax-Friedrichs 型の差分近似
が用いられる. それらは, ある不変領域を持つことが知られている.
まず, 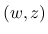 平面の三角領域
平面の三角領域
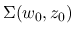 を以下のように定める.
を以下のように定める.
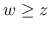 は
は  に対応し, これは常に満たす必要がある.
この
に対応し, これは常に満たす必要がある.
この
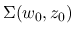 は
は 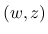 平面,
平面,  平面では
図 1 のようになる.
なお, これは
平面では
図 1 のようになる.
なお, これは  平面のものと
平面のものと 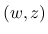 平面のものを同一視し, 同じ
平面のものを同一視し, 同じ
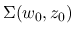 で表すことにする.
また, 厳密に言えば弱解は
で表すことにする.
また, 厳密に言えば弱解は 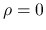 (
(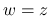 ) の値を取り得て, その部分では
) の値を取り得て, その部分では 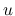 は未定義になってしまうのであるが, 弱解は正確には
は未定義になってしまうのであるが, 弱解は正確には  の対ではなく,
の対ではなく,
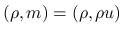 の対で考えるので,
の対で考えるので, 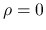 も問題なく弱解として含み得る.
本稿では, 弱解と
も問題なく弱解として含み得る.
本稿では, 弱解と 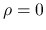 に関する議論は詳しくは行わないが, 参考文献[9] を参照のこと.
三角領域
に関する議論は詳しくは行わないが, 参考文献[9] を参照のこと.
三角領域
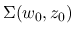 に関して次が成り立つことが知られている.
に関して次が成り立つことが知られている.
初期値これにより, この近似解の部分列がすべての
に対してある 三角領域
に含まれていれば, そこから構成する (3) の 人工粘性近似解, あるいは Lax-Friedrichs 型差分近似解
は,
に対し常に
に含まれる.
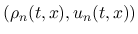 , その汎弱極限
, その汎弱極限
 , およびそれに対する Young 測度
, およびそれに対する Young 測度
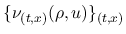 が
取れ,
が
取れ, 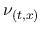 は
は
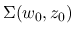 以外では 0 となる.
そして, 補償コンパクト性理論により, この Young 測度
以外では 0 となる.
そして, 補償コンパクト性理論により, この Young 測度 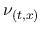 と, 任意の弱エントロピー対
と, 任意の弱エントロピー対 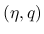 ,
,
 に対して, 冒頭の Tartar 方程式 (1) が, ほとんどいたるところの
に対して, 冒頭の Tartar 方程式 (1) が, ほとんどいたるところの 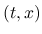 (
( ) に対して
成り立つことが示される.
ここまでは標準的な流れで, この部分に変更はない.
詳しくは参考文献[9] 等を参照のこと.
) に対して
成り立つことが示される.
ここまでは標準的な流れで, この部分に変更はない.
詳しくは参考文献[9] 等を参照のこと.
あとは, Tartar 方程式を解くのに必要な弱エンロピー対を, 以下のいわゆる Darboux の公式から具体的に生成して, それを使って考察する.
のとき, 実数上の任意の連続関数
に対して,
は, (5) を満たす弱エントロピー 対 () となる. ここで,
は

で,は
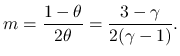
 は, 逆に
は, 逆に
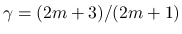 となり, DiPerna[3] は
となり, DiPerna[3] は  を自然数とし, Ding-Chen-Luo[2] は
を自然数とし, Ding-Chen-Luo[2] は  を 1 以上の実数としている.
本稿では,
を 1 以上の実数としている.
本稿では,  を自然数として, DiPerna[3] と同じ
を自然数として, DiPerna[3] と同じ  の
条件で考える.
の
条件で考える.
弱エントロピー対は, この Darboux の公式 (11) により, 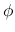 の自由度だけ存在し, ここから多くの種類のエントロピー対を生成できる.
この Darboux の公式の形のエントロピー対を, 本稿では「Darboux エントロピー対」と呼ぶ.
なお, 以後,
の自由度だけ存在し, ここから多くの種類のエントロピー対を生成できる.
この Darboux の公式の形のエントロピー対を, 本稿では「Darboux エントロピー対」と呼ぶ.
なお, 以後,
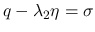 とする.
Darboux エントロピー対に対しては
とする.
Darboux エントロピー対に対しては
本稿の議論で必要なエントロピー対を以下に紹介する.
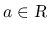 に対して,
に対して, 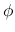 を
を 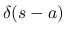 に近づけた極限, 具体的には
に近づけた極限, 具体的には
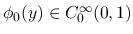 ,
,
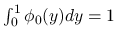 なる
なる  に対して
に対して
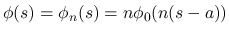 と
して
と
して
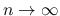 により得られるエントロピー対
ここで,
により得られるエントロピー対
ここで,  は
である (図 2). 詳しくは参考文献[9] を参照.
なお, このエントロピー対は, ほぼ Darboux の公式の積分を外して
は
である (図 2). 詳しくは参考文献[9] を参照.
なお, このエントロピー対は, ほぼ Darboux の公式の積分を外して 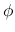 を除いた形なので, これを本稿では「核エントロピー対」と呼ぶ.
を除いた形なので, これを本稿では「核エントロピー対」と呼ぶ.
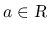 に対して,
に対して, 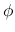 を
を 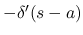 に近づけた極限, 具体的には上の
に近づけた極限, 具体的には上の  に対して
に対して
 と
して
と
して
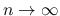 により得られるエントロピー対
により得られるエントロピー対
 は,
は,  では
では
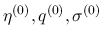 を
を 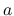 で微分したものになっている.
なお, 厳密に言えば,
で微分したものになっている.
なお, 厳密に言えば,
 は,
は, 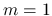 の場合は
の場合は 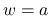 ,
, 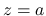 で連続ではないが,
で連続ではないが, 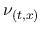 での積分は可能で,
での積分は可能で,
 に対して成立する Tartar 方程式で, Lebesgue 収束定理による極限を取れば,
に対して成立する Tartar 方程式で, Lebesgue 収束定理による極限を取れば,
 に対しても Tartar 方程式が成立することが
示される.
に対しても Tartar 方程式が成立することが
示される.
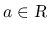 に対して
に対して
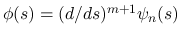 として得られる
弱エントロピー対
として得られる
弱エントロピー対  . ここで
. ここで 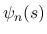 は
は
 で,
で, 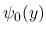 は
は 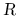 上滑らかで,
とする. そして同じ条件を満たす
上滑らかで,
とする. そして同じ条件を満たす
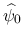 に対して,
に対して,  と同様にして構成した弱エントロピー対を
と同様にして構成した弱エントロピー対を
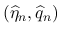 とし,
とし,
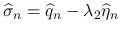 とする.
とする.
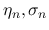 を計算する.
を計算する.

 では
では 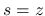 ,
,  で 0 になるので,
で 0 になるので,  回部分積分すると,
となる. ここで,
回部分積分すると,
となる. ここで,  は
の
は
の 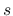 に関する多項式であり, その境界値は
となる.
もう 1 回部分積分をすると,
に関する多項式であり, その境界値は
となる.
もう 1 回部分積分をすると, 竹野茂治@新潟工科大学