
 の評価, およびその極限を考察する.
の評価, およびその極限を考察する.
本節では, (20) と (21) の
式を使って,  を一旦行列式形に表す.
を一旦行列式形に表す.
![$\displaystyle \overrightarrow{Q} = \left[\begin{array}{c}Q_1\\ Q_2\end{array}\r...
...overrightarrow{R}(s) = \left[\begin{array}{c}R_1(s)\\ R_2(s)\end{array}\right]
$](img281.png)
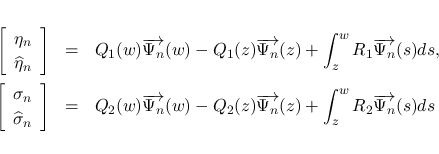
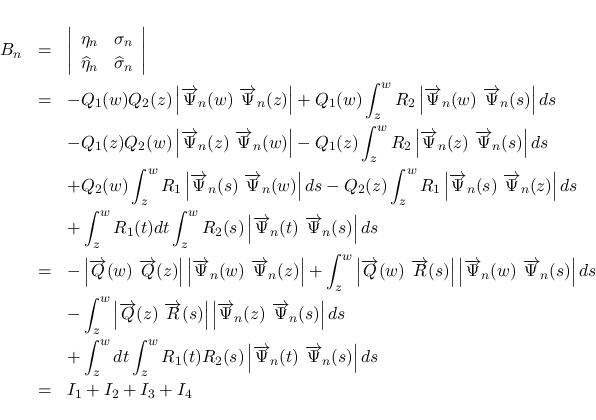
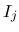 は, その前の式の項を一つずつ順番に
名付けることにする.
は, その前の式の項を一つずつ順番に
名付けることにする.
まずは  から考える. (19) より,
から考える. (19) より,
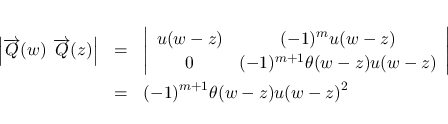
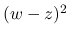 を因数に含むので,
を因数に含むので, 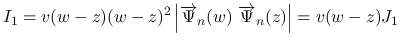
 で,
で,  ,
,  により
により
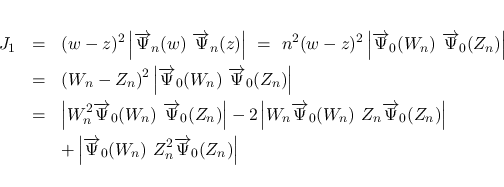
![$w,z,a\in [z_1,w_1]$](img259.png) に対する
に対する 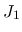 の一様有界性と 0 への収束性が
得られる. なお,
の一様有界性と 0 への収束性が
得られる. なお, ![$\displaystyle \overrightarrow{\Psi}_0(y)=\left[\begin{array}{c}\psi_0(y)\\ \widehat{\psi}_0(y)\end{array}\right]
$](img292.png)
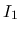 は一様有界で,
は一様有界で,
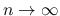 のときに 0 に
収束する.
のときに 0 に
収束する.
次は  を考える.
を考える.  は二重積分の形にまとめているが, 実際には,
は二重積分の形にまとめているが, 実際には, 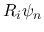 の積分と
の積分と
 の積分の積の差の形に
なっていて, よって,
の積分の積の差の形に
なっていて, よって,  の連続性と補題 3 により
の連続性と補題 3 により
![$w,z,a\in [z_1,w_1]$](img259.png) に対して一様有界で, その極限は,
に対して一様有界で, その極限は,
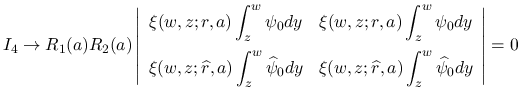
あとは  ,
, 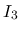 であるが, これらは 0 には収束しないので, 単独で考える代わりに, 連続関数
であるが, これらは 0 には収束しないので, 単独で考える代わりに, 連続関数  をかけて
をかけて 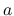 で
積分したものを考える.
まずは,
で
積分したものを考える.
まずは,  から.
から.
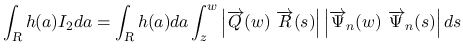
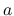 を
を  と置換し,
と置換し,  を
を  と置換すると,
と置換すると, 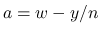 ,
, 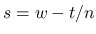 で,
で, 
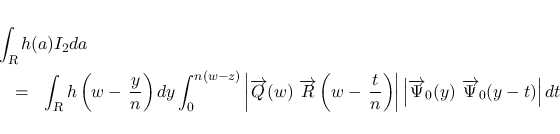
 より
より
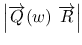 は
は
![$w,z\in[z_1,w_1]$](img309.png) に関して有界,
に関して有界, 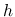 も有界で,
も有界で,
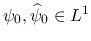 より
より

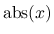 は
は 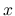 の絶対値), Lebesgue 収束定理により,
の絶対値), Lebesgue 収束定理により,  では
に収束し,
では
に収束し, 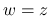 では 0 となることがわかる.
では 0 となることがわかる.
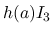 の積分も同様に,
の積分も同様に,
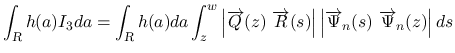
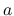 を
を 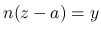 と置換し,
と置換し, 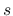 を
を 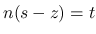 と置換すると,
と置換すると, 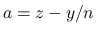 ,
, 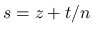 で,
で, 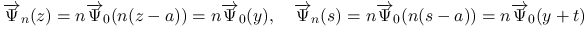
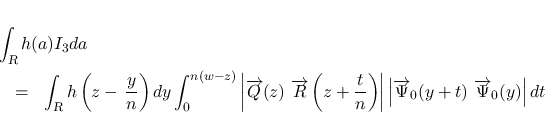
 の場合と同様に有界性が言え, その極限は,
の場合と同様に有界性が言え, その極限は,  では
に収束し,
では
に収束し, 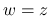 では 0 となる.
では 0 となる.
(34), (35) の極限の値を
求めるために, 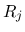 の
の 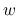 ,
, 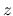 での値をまず計算する.
(18), (22) より,
での値をまず計算する.
(18), (22) より,
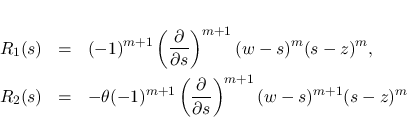
![\begin{eqnarray*}\left\vert\overrightarrow{Q}(w)\ \overrightarrow{R}(w)\right\ve...
...\ [.7zh]
w-z & m+1\end{array}\right\vert
\ =\
-\theta(m+1)u^2\end{eqnarray*}](img327.png)
 は, 置換して順序交換すれば,
は, 置換して順序交換すれば, 
 は
は
![$w,z\in[z_1,w_1]$](img309.png) に関して一様有界で,
となる.
に関して一様有界で,
となる.
 は
は ![$[z_1,w_1]$](img268.png) の外では 0 なので, Fubini の定理より,
の外では 0 なので, Fubini の定理より,
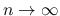 に対して
に対して

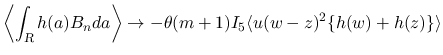
 となる
となる  ,
,
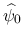 が取れれば,
が得られることになる.
が取れれば,
が得られることになる.
そのような  ,
,
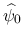 の存在は, 以下のように保証される.
例えば 0 ではない
の存在は, 以下のように保証される.
例えば 0 ではない 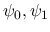 を
を
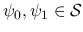 (= 急減少関数の族) で
(= 急減少関数の族) で
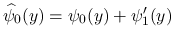 とすると, これらは (16) を満たし,
とすると, これらは (16) を満たし, 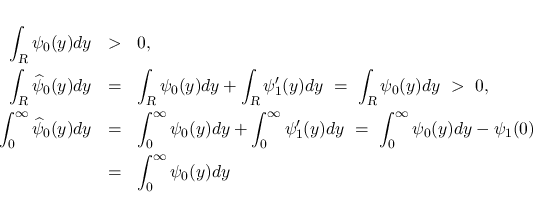
 となり, また
となり, また
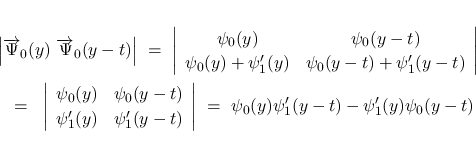
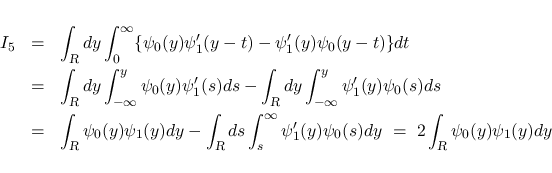
 となる.
実際に (40) を満たす
となる.
実際に (40) を満たす 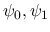 としては, 例えば
などがある.
としては, 例えば
などがある.
竹野茂治@新潟工科大学