7.1 誤差評価

6 節で見たように、 Glimm 差分近似解はある関数 $U(t,x)$ に収束する部分列を持つが、 この $U(t,x)$ が弱解であるかどうかは自明ではない。 この節では、それが弱解、 すなわち積分による関係式 (2.2) を満たすかどうかを考える。

各 $\phi(t,x)\in C_0^1([0,\infty)\times R)$ に対し、 $\mathop{\mathrm{supp}}\nolimits \phi\subset [0,T)\times(-M,M)$ となる正数 $T$, $M$ を取れば、 定理 6.2 により、

$$\int\!\!\!\int _{[0,T)\times(-M,M)}\vert U^{\Delta''_n}(t,x)-U(t,x)\vert dtdx \rightarrow 0$$

であり、よって

$$\begin{eqnarray*}\lefteqn{ \int\!\!\!\int _{[0,T)\times(-M,M)}\vert F(U^{\Delta... ...times(-M,M)}\vert U^{\Delta''_n}-U\vert dtdx &\rightarrow & 0\end{eqnarray*}$$

となるので、まず

$$\int\!\!\!\int _{t>0}\{\phi_t U^{\Delta''_n}+\phi_x F(U^{\De... ... \rightarrow \int\!\!\!\int _{t>0}\{\phi_t U+\phi_x F(U)\}dtdx$$

は成り立つ。

また、$\Delta x$ を十分小さくして、 $1/\Delta x>M+2\Delta x$ であるとすれば、 $\phi(0,x)$ が 0 でない範囲では $U^\Delta(0,x)=U_0(m\Delta x)$ となるので、

$$\begin{eqnarray*}\lefteqn{ \left\vert\int_R\phi(0,x)U^\Delta(0,x)dx -\int_R\phi... ...0,\cdot)\Vert _{C} 2\Delta x\mathop{\mathrm{TV}}\nolimits _R U_0\end{eqnarray*}$$

なので、 $\Delta x\rightarrow +0$ のときに、

$$\int_R\phi(0,x)U^\Delta(0,x)dx\rightarrow\int_R\phi(0,x)U_0(x)dx$$

が成り立つ。よって、後は、

$$E(\Delta x) = \int\!\!\!\int _{t>0}\{\phi_t U^\Delta+\phi_x F(U^\Delta)\}dtdx +\int_R\phi(0,x)U^\Delta(0,x)dx$$ (7.98)

が、 $\Delta x=\Delta x''_n$ のとき、 あるいはその部分列に対して 0 に収束することを言えばよい。

なお、逆にこれが成り立たなければ、 近似解はたとえ収束したとしてもそれは解ではないことを意味し、 すなわち「近似解」が近似になっていないことになる。 その意味で、(7.1) (またはその部分列) が 0 に収束することは、 近似解がちゃんと解を近似しているかどうかを示すことにもなるので、 この $E(\Delta x)$ の評価は 誤差評価 と呼ばれる。 ただし、「誤差」とは言っても、 実際に真の解との差を意味するわけではなく、 あくまで解の弱形式 (2.2) の意味での誤差であるから、 この値が小さいからといって近似解が真の解に近い状態であるとは限らない。

3.2 節で説明したように、 Glimm の差分においては無限個の確率変数の組 $\theta=(\theta_n)_n$ が意味を持ち、 これをランダムに取ることによってこの近似解が弱解に近づき、 よってこの誤差 $E$ が 0 に近づくことが期待される。 その意味で、$E$ は

$$E=E(\Delta x)=E(\Delta x,\theta,\phi)$$

と書いて考える方が適切となる。

また、6 節で考えた部分列や極限 (定理 6.2) では $\theta$ のことを考慮してはいなかったから、 各 $\theta$ 毎に近似解を収束させる列や極限が取れたことになり、 つまりそれらの列や極限も $\theta$ に依存していることになる。 この節では、さらにその極限が弱解となるような 「適切な」$\theta$ を取れることを示すことが目標となる。

まず、この $E$ を変形する。 $U^\Delta (t,x)$ は、$t=t_n$ 上、及び Riemann 問題の波のつなぎ目 (衝撃波や接触不連続の波の上、あるいは膨張波の端) を除いては滑らかで 方程式 (1.1) を満たす。よって

$$U^\Delta_t+F(U^\Delta)_x = 0\hspace{1zw}\mbox{a.e. in $(0,\infty)\times R$}$$

が成り立つので、これに $\phi(t,x)$ をかけて積分すると、

$$0 = \int\!\!\!\int _{t>0}\phi\{U^\Delta_t+F(U^\Delta)_x\} dtdx$$

$$= \int\!\!\!\int _{t>0}\{(\phi U^\Delta)_t+(\phi F(U^\Delta))_x\} dtdx -\int\!\!\!\int _{t>0}\{\phi_t U^\Delta+\phi_xF(U^\Delta)\} dtdx$$ (7.99)

となるが、この第 1 項は Green の定理により、

$${ \int\!\!\!\int _{t>0}\{(\phi U^\Delta)_t+(\phi F(U^\Delta))_x\}... ...nfty\int_{t_{n-1}}^{t_n}\int_R \{(\phi U^\Delta)_t+(\phi F(U^\Delta))_x\} dxdt}$$

$$= \sum_{n=1}^\infty\int_R \left[\phi U^\Delta(t,x)\right]^{t=t_n-0}_{t=t_{n-1}+0}dx$$

$${}+\sum_{n=1}^\infty\sum_{\sigma(t)}\int_{t_{n-1}}^{t_n} \left(-\... ...+\sigma'(t)\left[\phi U^\Delta\right]^{x=\sigma(t)+0}_{x=\sigma(t)-0} \right)dt$$ (7.100)

と変形できる。ここで、 $\sum_{\sigma(t)}$ は、$t_{n-1}<t<t_n$ 内の 不連続波 $x=\sigma(t)$ すべてに渡る和である。 しかし、それに関する積分は、Rankine-Hugoniot 条件 (2.7) により、

$$-\left[\phi F(U^\Delta)\right]+\sigma'(t)\left[\phi U^\Delta... ...[U^\Delta\right]-\left[F(U^\Delta)\right])\phi(t,\sigma(t)) =0$$

となるので、結局 (7.3) の式は、

$${ \int\!\!\!\int _{t>0}\{(\phi U^\Delta)_t+(\phi F(U^\Delta))_x\} dtdx}$$

$$= \sum_{n=1}^\infty\int_R\phi(t_n,x)\left[U^\Delta\right]^{t=t_n-0}_{t=t_n+0}dx -\int_R\phi(0,x)U^\Delta(+0,x)dx$$ (7.101)

となる。よって、(7.2), (7.4) より、

$$E = \int\!\!\!\int _{t>0}\{\phi_t U^\Delta+\phi_x F(U^\Delta)\}dtdx +\int_R\phi(0,x)U^\Delta(0,x)dx$$

$$= \sum_{n=1}^\infty\int_R\phi(t_n,x)\left[U^\Delta\right]^{t=t_n-0}_{t=t_n+0}dx$$ (7.102)

が得られることになる。

今、この (7.5) の右辺の和の各項を $E_n$ と書くことにする:

$$E_n = E_n(\Delta x,\theta,\phi) = \int_R\phi(t_n,x)\left[U^\Delta\right]^{t=t_n-0}_{t=t_n+0}dx, %\label{eq:error:E_n}$$ (7.103)

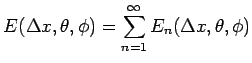$$E = E(\Delta x,\theta,\phi) = \sum_{n=1}^\infty E_n(\Delta x,\theta,\phi) %\label{eq:error:E_3}$$ (7.104)

[Glimm], [Smoller] では、$\phi$ を一旦階段関数で近似してから、 それに対する $E_n$ の $n$ に関する直交性を示して、 そこからその近似に関する評価を行っているが、 ここでは [Dafermos] に従ってそのままの $\phi\in C_0^1([0,\infty)\times R)$ に対して誤差評価を行う方法で 話を進めることにする。

$E(\Delta x,\theta,\phi)$ は、直接これが 0 に収束することを 示すことができるわけではなく、 確率変数 $\theta$ に関する平均が 0 に収束することを 示すことができるのみである。 よってそれを示すために、まずこの $E$ の「$\theta$ に関する積分」を考える。

各 $\theta_n$ は $-1<\theta_n<1$ であるので、 この範囲を確率測度空間にするために $\mu(d\theta_n) = (1/2)dx$, すなわち

$$E\subset (-1,1)\mbox{ に対して } \mu(E)=\frac{1}{2}m(E) \hspace{1zw}(\mbox{$m$ は Lebesgue 測度})$$

と定め、

$$X=\prod_{n=1}^\infty(-1,1)\ni\theta=(\theta_n)_n$$

に対して、この $\mu(d\theta_n)$ から導かれる 無限直積測度 $\nu(d\theta)$ を入れる。 例えば、 $X\supset\prod_{n=1}^\infty A_n$ に対しては、

$$\nu\left(\prod_{n=1}^\infty A_n\right) =\prod_{n=1}^\infty\mu(A_n) =\prod_{n=1}^\infty\frac{1}{2}m(A_n)$$

となる。詳しくは確率論の本、例えば [西尾] を参照のこと。

まずは、$\vert E_n\vert$ の評価を考える。

$$\begin{eqnarray*}\lefteqn{\vert E_n(\Delta x,\theta,\phi)\vert \leq \Vert\phi... ...)\Vert _{C}\mathop{\mathrm{TV}}\nolimits _R U^\Delta(t_n-0,\cdot)\end{eqnarray*}$$

となるので、(5.28) より

$$\vert E_n(\Delta x,\theta,\phi)\vert \leq 2C_1\Delta x\Vert\phi(t_n,\cdot)\Vert _{C}\mathop{\mathrm{TV}}\nolimits _R U_0$$ (7.105)

が得られる。

また、$E_n$ を $\theta_n$ で積分すると、

$$\begin{eqnarray*}\lefteqn{\int_{-1}^1 E_n(\Delta x,\theta,\phi)\mu(d\theta_n) =... ...^\Delta(t_n-0,\cdot)\right]^x_{(m+\theta_n)\Delta x} dxd\theta_n\end{eqnarray*}$$

ここで、$\theta_n$ に関する積分を $y=(m+\theta_n)\Delta x$ と置換すれば、

$${\int_{-1}^1 E_n(\Delta x,\theta,\phi)\mu(d\theta_n)}$$

$$= \frac{1}{2\Delta x}\sum_{m} \int_{(m-1)\Delta x}^{(m+1)\Delta x}\... ...Delta x}^{(m+1)\Delta x} \phi(t_n,x)\left[U^\Delta(t_n-0,\cdot)\right]^x_y dxdy$$ (7.107)

となるが、

$$\begin{eqnarray*}\lefteqn{ \int_{(m-1)\Delta x}^{(m+1)\Delta x}\int_{(m-1)\Delt... ...int_{(m-1)\Delta x}^{(m+1)\Delta x}U^\Delta(t_n-0,y)dy &=& 0\end{eqnarray*}$$

なので、

$${ \int_{(m-1)\Delta x}^{(m+1)\Delta x}\int_{(m-1)\Delta x}^{(m+1)\Delta x} \phi(t_n,x) \left[U^\Delta(t_n-0,\cdot)\right]^x_y dxdy}$$

$$= \int_{(m-1)\Delta x}^{(m+1)\Delta x}\int_{(m-1)\Delta x}^{(m+1)\D... ...\{\phi(t_n,x)-\phi(t_n,m\Delta x)\} \left[U^\Delta(t_n-0,\cdot)\right]^x_y dxdy$$ (7.108)

と変形できる。 $(m-1)\Delta x\leq x\leq (m+1)\Delta x$ では、

$$\vert\phi(t_n,x)-\phi(t_n,m\Delta x)\vert \leq \Vert\phi_x(t_n,\cdot)\Vert _{C}\Delta x$$ (7.109)

と評価できるので、よって (7.10), (7.11), (7.12) により、

$$\begin{eqnarray*}\lefteqn{\left\vert\int_{-1}^1 E_n(\Delta x,\theta,\phi)\mu(d\t... ...\Vert _{C}\mathop{\mathrm{TV}}\nolimits _R U^\Delta(t_n-0,\cdot) \end{eqnarray*}$$

となる。よって、

$$\left\vert\int_{-1}^1 E_n(\Delta x,\theta,\phi)\mu(d\theta_... ...\phi_x(t_n,\cdot)\Vert _{C}\mathop{\mathrm{TV}}\nolimits _R U_0$$ (7.110)

となる。

自然数 $n_0$ を、 $n_0\Delta t<T\leq (n_0+1)\Delta t$ なるものとすると $n>n_0$ に対して $\phi(t_n,x)\equiv 0$ であり、 そのような $n$ に対しては $E_n=0$ となるので、

$$E(\Delta x,\theta,\phi)=\sum_{n=1}^{n_0}E_n(\Delta x,\theta,\phi)$$

であり、よって $n>n_0$ に対する $\theta_n$ は $E(\Delta x,\theta,\phi)$ の中には現れない。 よって、$\vert E\vert^2$ を $X$ で積分すると、

$$\begin{eqnarray*}\lefteqn{\int_X\vert E(\Delta x,\theta,\phi)\vert^2\nu(d\theta)... ...\Delta x,\theta,\phi)\right\vert^2 d\theta_1\cdots d\theta_{n_0}\end{eqnarray*}$$

となる。ここで、

$$\left\vert\sum_{n=1}^{n_0}E_n\right\vert^2 = \left(\sum_{... ...}\vert E_n\vert^2 +2\sum_{n_1<n_2\leq n_0}E_{n_1}\cdot E_{n_2}$$ (7.111)

と分けると、 $n>k$ のとき $E_k$ は $\theta_n$ に関しては定数なので、 この $\vert E_n\vert^2$ の和に関する積分は (7.8) より、

$$\begin{eqnarray*}\lefteqn{\frac{1}{2^{n_0}}\int_{-1}^1\cdots\int_{-1}^1 \sum_{n... ...C([0,\infty)\times R)}^2 (\mathop{\mathrm{TV}}\nolimits _R U_0)^2\end{eqnarray*}$$

と評価できる。ここで、 $n_0\Delta x=n_0\Delta t\Lambda\leq T\Lambda$ なので、結局

$$\frac{1}{2^{n_0}}\int_{-1}^1\cdots\int_{-1}^1 \sum_{n=1}^{... ...[0,\infty)\times R)}^2(\mathop{\mathrm{TV}}\nolimits _R U_0)^2$$ (7.112)

となる。 一方、 $E_{n_1}\cdot E_{n_2}$ の和の積分は、

$$\begin{eqnarray*}\lefteqn{\frac{1}{2^{n_0}}\int_{-1}^1\cdots\int_{-1}^1 2\sum_{... ...ots\int_{-1}^1 E_{n_1}\cdot E_{n_2}d\theta_{n_2}\cdots d\theta_1\end{eqnarray*}$$

と書け、$n_1<n_2$ なので、 (7.8), (7.13) より、

$$\begin{eqnarray*}\lefteqn{\left\vert\frac{1}{2}\int_{-1}^1E_{n_1}\cdot E_{n_2}d\... ...hi(t_{n_1},\cdot)\Vert _{C} \Vert\phi_x(t_{n_2},\cdot)\Vert _{C}\end{eqnarray*}$$

となるので、よって、

$$\begin{eqnarray*}\lefteqn{\left\vert\frac{1}{2^{n_0}}\int_{-1}^1\cdots\int_{-1}^... ..._{C}\Vert\phi_x\Vert _{C}(\mathop{\mathrm{TV}}\nolimits _R U_0)^2\end{eqnarray*}$$

となるので、 $n_0\Delta x\leq T\Lambda$ より

$${\left\vert\frac{1}{2^{n_0}}\int_{-1}^1\cdots\int_{-1}^1 2\sum_{n_1<n_2\leq n_0}E_{n_1}\cdot E_{n_2} d\theta_1\cdots d\theta_{n_0}\right\vert}$$

$$\leq 2C_1^2(T\Lambda)^2\Delta x \Vert\phi\Vert _{C}\Vert\phi_x\Vert _{C}(\mathop{\mathrm{TV}}\nolimits _R U_0)^2$$ (7.113)

となる。 よって、(7.14), (7.15), (7.16) より、

$${\int_X\vert E(\Delta x,\theta,\phi)\vert^2\nu(d\theta)}$$

$$\leq 4T\Lambda(C_1\mathop{\mathrm{TV}}\nolimits _R U_0 \Vert\phi\Vert ... ...hi\Vert _{C}\Vert\phi_x\Vert _{C}\Delta x %\label{eq:error:\vert E\vert^2_est}$$ (7.114)

が得られるから、 $\Delta x\rightarrow +0$ のとき

$$\int_X\vert E(\Delta x,\theta,\phi)\vert^2\nu(d\theta)\rightarrow 0$$

となることがわかる。 つまり、 $E(\Delta x,\theta,\phi)$ は、 $L^2(X;\nu(d\theta))$ で 0 に収束することになるので、 通常の Lebesgue 積分の理論により、 0 に a.e. 収束する $E(\Delta x,\theta,\phi)$ の部分列が存在することが示される。 つまり、ある $N_\phi\subset X$ と 0 に収束する列 $\{\Delta\bar{x}_n(\phi)\}_n$ (それぞれ $\phi$ に依存するが $\theta$ にはよらない) がとれて、 $\nu(N_\phi)=0$ で、かつ $\theta\in X\setminus N_\phi$ に対して

$$E(\Delta\bar{x}_n(\phi),\theta,\phi)\rightarrow 0$$

となる。 この $N$ や部分列の $\phi$ への依存性をなくすために次の事実を用いる。

補題 7.1

$C_0^\infty([0,\infty)\times R)$ のある可算部分集合列 $\{\phi_n\}_n$ があって、 任意の $\phi\in C_0([0,\infty)\times R)$ に対し、 ある部分列 $\{\phi_{n_j}\}_j$ が取れて次を満たす。

1. $j$ によらないある正数 $T_0$, $M_0$ が存在して、

   $$\mathop{\mathrm{supp}}\nolimits \phi_{n_j}, \mathop{\mathrm{supp}}\nolimits \phi\subset [0,T_0)\times(-M_0,M_0)$$

   
   
2. $j\rightarrow\infty$ のとき、

   $$\Vert\phi_{n_j}-\phi\Vert _{C}\rightarrow 0$$

   
   

これは、任意の連続関数がコンパクト集合上多項式で一様近似できること (Weierstrass の定理) と、 $[0,n]\times[-m,m]$ 上 1 で $C^\infty_0$ の元であるような 関数列 $\psi_{n,m}(t,x)$ を使えば容易に示せるので証明は省略する。

この補題 7.1 の $\phi_k$ に対する $N_{\phi_k}$ を考えると、その和 $N=\bigcup_k N_{\phi_k}$ も 0 集合 ($\nu(N)=0$) であり、 一方部分列の方は、この $\{\phi_k\}$ に関して次のような部分列の列を作る:

$$\{\Delta\bar{x}'_n(1)\} \supset \{\Delta\bar{x}'_n(2)\} \supset \{\Delta\bar{x}'_n(3)\} \supset\ldots$$

で、任意の $k$ と $\theta\in X\setminus N_{\phi_k}$ に対して、

$$\lim_{n\rightarrow\infty}E(\Delta\bar{x}'_n(k),\theta,\phi_k)=0$$

となるものとする。 対角線論法を用いれば、 $\theta\in X\setminus N=\bigcap_k(X\setminus N_{\phi_k})$ に対しては任意の $k$ に対して

$$\lim_{n\rightarrow\infty}E(\Delta\bar{x}'_n(n),\theta,\phi_k)=0$$ (7.115)

となることが言える。

このとき、任意の $\phi\in C_0^1([0,\infty)\times R)$ に対して、 補題 7.1 の $\{\phi_{n_j}\}_j$ と $T_0$, $M_0$ を取れば、(7.8) により、

$$\begin{eqnarray*}\lefteqn{\vert E(\Delta\bar{x}'_n(n),\theta,\phi)\vert \leq ... ...\Vert _{C} +\vert E(\Delta\bar{x}'_n(n),\theta,\phi_{n_j})\vert \end{eqnarray*}$$

となるので、 $n\rightarrow\infty$ の上極限を取れば、 (7.18) より

$$\limsup_{n\rightarrow\infty}\vert E(\Delta\bar{x}'_n(n),\the... ...hop{\mathrm{TV}}\nolimits _R U_0\Vert\phi-\phi_{n_j}\Vert _{C}$$

となるが、 $j\rightarrow\infty$ とすれば右辺は 0 に収束するので、 結局 $\theta\in X\setminus N$ に対して

$$\lim_{n\rightarrow\infty}E(\Delta\bar{x}'_n(n),\theta,\phi)=0$$

となる。

この $\{\Delta\bar{x}'_n(n)\}_n$ に対し、 6 節の議論を用いてある $U(t,x)$ に収束する部分列 $\{\Delta\tilde{x}_n\}_n$ を取れば、 $\theta\in X\setminus N$ に対してはその極限 $U$ が 弱解になることが言えたことになる。