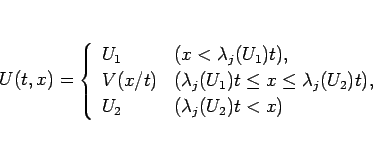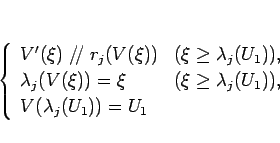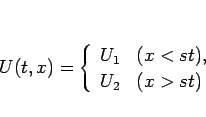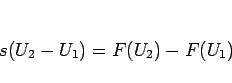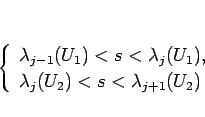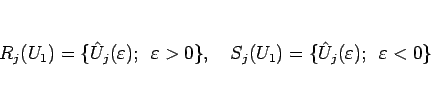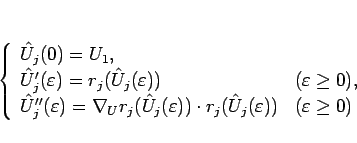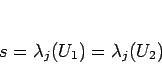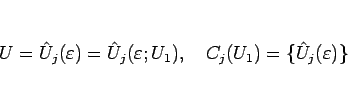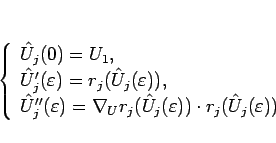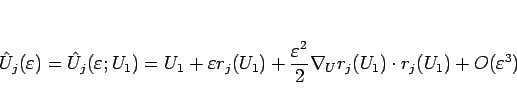(2.7)
ここで、
(2.8)
を満たす関数。 各
![]() は、(2.6) を満たす
は、(2.6) を満たす
![]() の値の集合でもあり、
ベクトル場
の値の集合でもあり、
ベクトル場 ![]() の積分曲線 (の一部) でもあり、
また、
の積分曲線 (の一部) でもあり、
また、![]() を左から右に見ていくと、
膨張波解の値がこの
を左から右に見ていくと、
膨張波解の値がこの ![]() 上を連続的に移動することもわかる。
上を連続的に移動することもわかる。
ここで、
(2.9)
と Lax 条件:
(2.10)
(ただし、
![]() に対し、この
に対し、この ![]() の取りうる集合 (
の取りうる集合 (![]() から始まる半曲線)
を
から始まる半曲線)
を ![]() と書いて 衝撃波曲線 と呼ぶ。
と書いて 衝撃波曲線 と呼ぶ。
![]() と
と ![]() は
は ![]() で
で ![]() 級でつながり、
級でつながり、
![]() パラメータ
パラメータ ![]() を使って、
以下のものを満たすものとして
を使って、
以下のものを満たすものとして
![]() と書ける:
と書ける:
(2.11)
(詳しくは、例えば [竹野] 参照)。
ここで、
(2.12)
を満たすもの。
(2.13)
を満たすものと書ける。