6.2 (t,x) に対する極限
(6.4) と Lebesgue 有界収束定理を用いれば、
任意の正数  ,
, 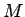 に対して、
に対して、

も言えるので、
ある
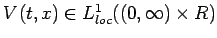 が存在して、
任意の正数
が存在して、
任意の正数  ,
, 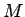 に対して、
に対して、
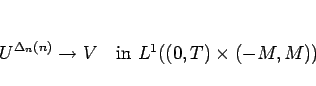
が言える。
よって、(必要ならば対角線論法を用いて)
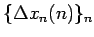 のある部分列
のある部分列
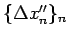 を取って、
を取って、
 |
(6.93) |
とできるので、(6.5), (6.6),
(6.7) より、
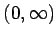 のある 0 集合
のある 0 集合 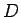 に対して、
に対して、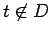 ならば
ならば

となることが言える。よって 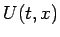 を、
を、
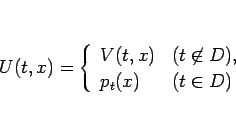
と定義すれば、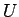 は 0 集合
は 0 集合 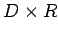 以外では
以外では  に等しいから
に等しいから
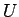 は
は  に関する可測関数であり、
すべての
に関する可測関数であり、
すべての 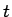 に対し、
に対し、
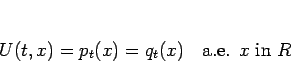 |
(6.94) |
を満たすことになる。さらにこの 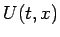 は、
定理 5.2 と
Helly の定理 6.1 により、
次も満たすことになる:
は、
定理 5.2 と
Helly の定理 6.1 により、
次も満たすことになる:
ただし、この (6.9) のように
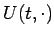 を有界変動関数と見るときは、
ここでは (6.8) により
を有界変動関数と見るときは、
ここでは (6.8) により
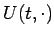 の代わりに
の代わりに  を考えることを意味するものとする3。
を考えることを意味するものとする3。
Helly の定理 6.1、および 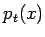 の定義により、
の定義により、
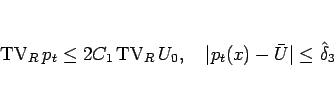
であるから、(6.8) により
(6.9), (6.10) が得られるので、
最後に (6.11) を示す。
(5.30) より、任意の 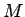 に対して
に対して

であり
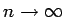 とすれば、(6.4) より
とすれば、(6.4) より
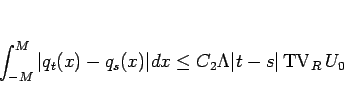
となり、よって (6.8) により

となる。
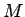 は任意なので、よって (6.11) が得られる。
は任意なので、よって (6.11) が得られる。
以上をまとめると、以下のようになる。
定理 6.2
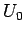 に関する定理 5.1 の仮定の下、
0 に収束するある列
に関する定理 5.1 の仮定の下、
0 に収束するある列
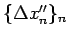 に対して、
これに対する近似解
に対して、
これに対する近似解
 はほとんどいたるところ
ある関数
はほとんどいたるところ
ある関数
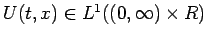 に収束し、
この
に収束し、
この 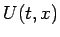 は (6.9),
(6.10), (6.11) を満たす。
は (6.9),
(6.10), (6.11) を満たす。
ただし、
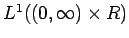 の元
の元 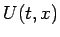 の
の
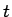 での値
での値 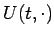 というのは、
本来はほとんどいたるところの
というのは、
本来はほとんどいたるところの 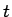 にしか意味はないが、
この定理での
にしか意味はないが、
この定理での 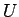 の値に関する性質に関しては、
上に述べてきたように、
すべての
の値に関する性質に関しては、
上に述べてきたように、
すべての 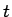 (および
(および 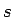 ) に対してこれらの性質
(6.9), (6.10),
(6.11)
が意味を持つような
) に対してこれらの性質
(6.9), (6.10),
(6.11)
が意味を持つような
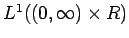 の代表元を取ることができる、
といったような意味合いであることに注意する。
の代表元を取ることができる、
といったような意味合いであることに注意する。
竹野茂治@新潟工科大学
2009年1月18日
![]() の定義により、
の定義により、
![]() に対して
に対して
![]() に関する定理 5.1 の仮定の下、
0 に収束するある列
に関する定理 5.1 の仮定の下、
0 に収束するある列
![]() に対して、
これに対する近似解
に対して、
これに対する近似解
![]() はほとんどいたるところ
ある関数
はほとんどいたるところ
ある関数
![]() に収束し、
この
に収束し、
この ![]() は (6.9),
(6.10), (6.11) を満たす。
は (6.9),
(6.10), (6.11) を満たす。
![]() の元
の元 ![]() の
の
![]() での値
での値 ![]() というのは、
本来はほとんどいたるところの
というのは、
本来はほとんどいたるところの ![]() にしか意味はないが、
この定理での
にしか意味はないが、
この定理での ![]() の値に関する性質に関しては、
上に述べてきたように、
すべての
の値に関する性質に関しては、
上に述べてきたように、
すべての ![]() (および
(および ![]() ) に対してこれらの性質
(6.9), (6.10),
(6.11)
が意味を持つような
) に対してこれらの性質
(6.9), (6.10),
(6.11)
が意味を持つような
![]() の代表元を取ることができる、
といったような意味合いであることに注意する。
の代表元を取ることができる、
といったような意味合いであることに注意する。