私の修士論文 (1990 年 2 月) です。 私の頃はまだ手書きでしたので、 スキャナで取りこんだものを無理矢理 PS, PDF にしたものなので、 画質はよくありませんし、ファイルサイズも大きいです (12.5MB, 8.7MB)。 HTML は、その画像を単に 1 枚ずつ貼りつけたものです。
内容は、等エントロピー流のピストン問題の大域解の存在を、 compensated compactness を使って証明したものですが、 この結果を拡張したものが後に Proc.Royal.Soc.Edinburgh に掲載されました。 ただし、この修士論文は
以前研究会のために準備した compensated compactness に関する 本、論文などを整理した物です。 今となってはやや古くなりましたが、 基本的な物は現在でもそう変化はなく参考になると思います。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
研究室の 4 年生のために書いた非線形双曲形偏微分方程式の入門書です。 ただし、かなりかたよった話になっています。
HTML 版は図の大きさがまちまちで、文字が切れている部分があるので 調整する予定でしたが、それなりに見えますので公開します。 ちゃんと見たい場合は PostScript 版、PDF 版の方をどうぞ。
HTML 版に PDF ファイルへのリンクを追加し、 画像の背景の色がおかしくなっているものを修正しました (01/13 2009)。
(単独保存則方程式 + 時間周期外力) の方程式の時間周期解の存在を compensated compactness を用いて、なるべく一般的な条件の元で 証明したものです。 これを連立方程式 (等エントロピー理想気体) の場合に拡張するのが 現在の私の主要なテーマの一つです。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
最近興味を持っている保存則方程式の周期解に関して、 単独方程式の場合の数値計算をしてその様子を見てみたものです。 元は研究室の学生向けに卒業研究のための資料として書いたものですが、 私自身の数学的な研究にももちろん意味があります。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
単独保存則方程式に対する compensated compactness 入門といった内容です。 2001 年 6 月に京都大学数理研で話したものをまとめたものです。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
以前工科大紀要に書いた、 「単独保存則方程式の周期解の数値解析」 の続編です。 前の論文で不明であった周期解の構造を数値的に解明したもので、 共同研究により明らかになった数学的な結果も合わせて紹介しています。 今後もこの論文で明らかになった数値的な結果を 一般の状況で数学的に証明すること、 及びここで取り上げられている数学的な結果を発展させることを 考えていきたいと思っています。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
N×N のリーマン問題の話は、あまり日本語の解説もなさそうだったので、 春休みを利用して入門書として書いてみました。 ただし、うだうだ書いたためにかなり長くなってしまいました (140 ページ程)。
ちゃんと見たい場合は PostScript 版、PDF 版の方をどうぞ。
目次をつけて、2,3 の修正を行いました (08/18 2007)。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
Glimm 差分の話を、自分の勉強も兼ねて、夏休みを利用して書いてみました。 最初は「入門」としようと思っていたのですが、 N=2 などに限定してもあまり簡単になるわけではなかったので 「解説」としてみました (75 ページ程)。
手法は、Glimm の原論文よりも、 Dafermos の本 流の手法による解説になっています。 ちゃんと見たい場合は PostScript 版、PDF 版の方をどうぞ。
HTML 版に PDF ファイルへのリンクを追加しました (01/13 2009)。
相互作用評価の 4 節 (4.1, 4.3 節) の引用文献の [Yong] と書くべきところを [Lu] と書いていましたので修正しました (Thanks Wen-An Yong)。
上の 単独保存則の時間周期解の論文 は、compensated compactness を用いて周期解の存在を示していますが、 その中でキーとなるのは単独保存則方程式の Lax-Friedrichs 差分近似解の、 周期外力がない場合の一様減衰評価です。 そのキーとなる一様な減衰評価を、 多分差分よりはわかりやすい人工粘性近似解に対して説明しています (実質的に同じです)。 ついでに、連立方程式で同じ方法を用いようとすると どうなるかについても簡単に述べています。
既知の結果の解説が主ですが、 保存則方程式の減衰を考える場合の何かの参考になれば、と思います。
上の 「compensated compactness と保存則方程式について」 では、単独保存則方程式に関する補償コンパクト法 (compensated compactnes method) の解説を行いましたが、これは 2x2 の保存則方程式である 1 次元の等エントロピー気体の運動方程式に対する補償コンパクト法についての 解説を書きました。
ここでは比熱比γ=5/3 の場合に限っての解説を行いましたが、 以下の点が上の 修士論文 とは違っています。
よって 修士論文 よりは 多少わかり易いのではないかと思います。
追記 (12/14 2010):
最近、この続きをやっていて、ψ0 を、 サポートが (0,1) 内の関数で考えるよりも、 むしろ L1 で遠方の減衰を持つ (|x|→∞ のときに x2ψ0→ 0) という仮定で考えた方が少しシンプルに議論できそうなことがわかりました (p41-p43 付近)。機会があったら補遺としてでもまとめたいと思います。
ここでは、conservation law に関する Q and A を取り上げます。 実際に今までに受けた質問や、必要と思われる物などを取り上げていく予定です。
もし、conservation law に関する質問があれば メールをください。 Q and A として適当なものがあればここに載せていく予定です。
また、この Q and A に誤り、修正が必要な箇所を見つけた場合は 報告してください。
ご意見、ご希望なども歓迎します。
(06/05 2001)
現在 (06/05 2001) は 竹野茂治 (shige)が 個人的に作っています。よって、内容も shige の知る所によってのみ 書かれていますから、必ずしも正しい物ではないかも知れません。 間違いや改良箇所などを見つけたら、是非 御連絡下さい。
(06/05 2001)一応研究しています。なかなか結果は出ませんが、現在 (08/06 2001) まで 10 年以上は研究していることになります。
(08/08 2001)解の存在を証明する方法 (QandA 4.6 を参照) として 補完測度法 (compensated compactness theory; 補償コンパクト性理論とも呼ばれる) というものがありますが、 いくつかの方程式に対してこれを使って解の存在を証明するための研究や、 補完測度法の適用部分の改良などの研究を行っています。
これまでは主に、1 次元の等エントロピー気体の方程式の初期値境界値問題、 3 次元の星の大気、あるいは気体星の球対称解の存在、 1 次元非線形弾性振動の方程式の弱解 (方程式については QandA 2.2 を参照) の研究を行ってきました。
最近では、周期外力を持つ conservation law の周期解の存在や性質に 興味があり、 それに関する研究 (工科大紀要の論文 I, 工科大紀要の論文 II 参照) も行っています。
(08/08 2001; 12/20 2004, 03/27 2007 修正)元々、気体や液体などの流体の運動を支配する方程式から来ていて、 これらは、質量保存則、運動量保存則、エネルギー保存則などの物理量の 保存則から導かれるのでそのような名前がついています。
そしてそれを一般化した方程式系
を、conservation law (保存則方程式) といいます。 通常研究されているのは 1 次元の保存則方程式系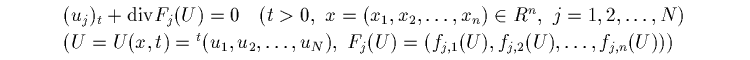
で、かつ双曲型と呼ばれる物です。 双曲型とは、準線形の形の方程式に直したもの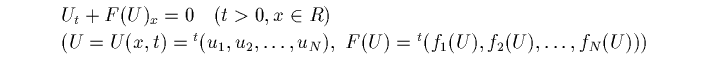
の係数行列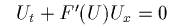
の固有値がすべて実数で相異なるものをいいます。 (06/05 2001)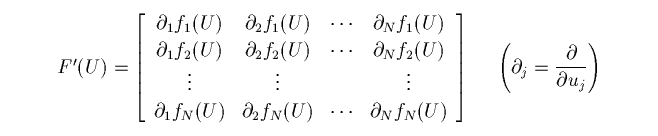
は、単独保存則方程式の典型的なものの一つです。 元々は、粘性バーガース方程式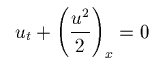
の、粘性係数νを 0 にしたもののようです。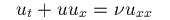
ただし、これは解析が難しいので、圧力 P が v のみの関数 P=P(v) である場合 (バロトロピック) を考え、最初の 2 本で閉じた方程式系と 考えたもの
(u: 速度, v=1/ρ: 比体積, ρ: 密度, P: 圧力, e: 内部エネルギー)
がよく研究されています。これは特に P-system と呼ばれます。 P=P(v) は P'(v)<0, P''(v)>0 のような仮定がおかれることが 多いようですが、特に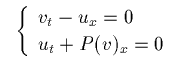
P=A/v (等音気体, A>0: 定数),がよく研究されています。 Euler 座標系では
P=A/vγ (等エントロピー気体, A>0,γ>1: 定数)
のようになります。これも P=P(ρ) と考え、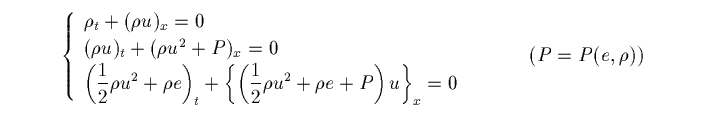
としたものが良く研究されています。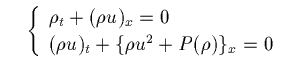
のようなものがありますが、これは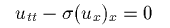
のように書き直すことができます。通常は σ'(w)>0 を仮定します。 P-system と似た形をしていますが、w は負の値も取り得ます。 どちらかというと w と σ''(w) が同符号である場合より、 w と σ''(w) が異符号である方程式の方が難しいようです。
が成り立ちますが、この速度 u がρのみの関数 u=u(ρ) であると見ると 単独保存則方程式となります。この場合は、
(u: 速度, ρ>0: 密度)
0≦ρ≦R (=最大密度), u(0)=u(R)=0, u'(ρ)≦0などが自然な条件であるようです。 さらに u と ρ の関係を運動方程式によって関係付けて、 気体の質量保存と運動量保存の、2x2 の連立方程式と同等の形とする 交通流モデルもあるようです。
これは、気体の等エントロピー流の方程式の γ=2 の場合に相当します。
(g: 重力加速度、h: 水深、u: 速度)
ここで、f(u),g(v),h(w) (w=1-u-v) は
(u, v, 1-u-v: 油、水、ガスの体積率)
f(0)=f'(0)=g(0)=g'(0)=h(0)=h'(0)=0,を満たすのが自然であるようです。例えば f=au2, g=bv2, h=cw2 のような形です。
f''(u)>0, g''(v)>0, h''(w)>0
最近は conservation law の教科書も増えて来ました。 例えば次のような物があります。
他にも、保存則系について概説してある日本語の記事に次のような物があります。
また、この方程式の数値計算は衝撃波があるため難しい所もあるのですが、 色々詳しく調べられていて、現在もなお活発に研究されています。 数値計算に関しては例えば次をご覧下さい。
保存則方程式に関する最新の研究に関しては、 国際会議の会議録 (特に 2 年に 1 度の "Hyperbolic Problems: Theory, Numerics, Applications" が有名) がたくさん出版されていますし、プレプリントサーバもあります。
難しい質問ですね。
私は双曲型の、空間次元が 1 次元の物しか良くは知りませんが、 例えば空間次元が 3 以上の物については、連立方程式に対しては 数学的にはほとんど何も分かっていないでしょう。 空間に関して球対称と仮定して、動径方向のみの 1 次元形にした物に対する 結果ならありますが。
空間次元が 2 次元の場合も、連立方程式の場合はほとんど何も解かれていない と言ってもいいでしょう。まだ Riemann 問題が研究されている段階です。
連立でない、単独の方程式 (N=1) に対しては、空間次元が 2 以上の場合も 色々 (解の存在、一意性、初期値に関する連続性なども ?) 分かって いるようですが、私は詳しくは知りません。
最もよく研究されているのが空間 1 次元の場合です。 例えば気体の方程式でいうと、細長い管に気体が入っていて、右へ行くか 左へ行くかの運動しか考えない、非粘性の気体の運動に相当します。
初期値問題は、十分定数に近い初期値に対しては時間大域的な弱解 (エントロピー解) の存在が示されていて、漸近的な挙動も多少 知られています。
しかし、大きい初期値、またはエントロピー解の一意性については 連立方程式ではまだ部分的にしか結果はありません。
(06/05 2001)真性非線形 (genuinely nonlinear) であるような双曲型保存則の方程式では、 初期値が滑らかでも解が有限時刻で不連続になる現象が知られています。 実際にもこれに対応する物理現象があり、衝撃波と呼ばれています。
もちろん、衝撃波が発生した後も現象は続いているわけですから、そのような 不連続性を持つような (微分できないような) 解を考えなければいけません。
そのために、弱解、エントロピー解といった解を考える必要があるわけですが、 その解のクラスでは解の微分可能性が使えないため、通常他の方程式の 解の存在証明で使われるような不動点定理、ソボレフの不等式などが使えません。 そのため、使える道具が少なく、解の性質を調べるのも難しいのだと思います。
(06/05 2001)私は全体を知っているわけではないので、詳しくは知らないのですが、 私の知る限りで、以下のものを予想としてあげておきます。 いずれも空間 1 次元の conservation law 方程式に関するものです。
また、別の項目 (「QandA 2.4 知られていること」, 「QandA 4.3 一意性について」, 「QandA 4.4 初期値に関する連続性」, 「QandA 4.5 漸近性」) などもご覧下さい。
以上はいずれもかなり大きなものですが、他にも専門書や論文を読んで 専門家になれば細かい予想などが見えてくると思います。
(08/08 2001)一つ追加します。これも空間 1 次元に関する問題です。
連立方程式の場合も、いくつかの方程式に対しては compensated compactness によって解の存在が示されましたが、 この方法では初期値は必ずしも有界変動である必要はありません。 しかし、その弱解が t>0 に対して有界変動となるかどうかは 多分まだ分かっていないと思います (特に、大きな初期値に対して)。 compensated compactness では、近似解として人工粘性解や、 粘性を含む差分近似解が使われるのですが、 連立方程式の場合にはその一様有界変動評価を得るのが難しく、 まだ t>0 で有界変動となるかどうかは知られていないと思います。 最近 Bressan らが詳しく研究していて、 それに関する結果が少しずつ出て来てはいるようです。
(10/14 2002)とりあえず、今現在 (2008 04/01) では それなりに研究されていると言っていいと思います。
保存則方程式のプレプリントサーバ
しかも、conservation law に関する論文は、
ここに載らないものもかなりあって、
私も順次雑誌の目次を参照して論文のコピーを取りよせています。
難しくて研究が進まないテーマも多い中、
よくネタがつきないものだ、解決される問題もあるものだとも
思うほどです。
# 私も頑張んないと...
保存則方程式は日本国内にも何人か研究者がいる (Q 2.3. に上げた書物や記事などを書いた人以外にもいます) のですが、その多くが理学部数学科以外の所属だったりします。 数学的な理論家ではなく、実在する衝撃波研究といった工学的な立場、 あるいは流体の数値解析研究といった立場から研究している研究者もいます。 よって、どこというのは実はかなり難しいです。
また数学者は、割と所属を移動しがちなので、 知らないうちに別なところに行ってしまうこともよくありますし、 それに私からこの人とこの人、 という風に指定はしづらいところもあります。
ただ、理学部数学科の学部レベル (1-4 年生) では、 ここまで専門的な勉強をすることはあまりないと思いますので、 多分このような質問の意味が出てくるのは大学院の話だと思いますが、 流体に関する微分方程式を研究しておられる先生ならば、 保存則方程式に関しても理解があると思いますし、 大学院生ならば自分の興味のあることをそれなりに自由に勉強できるでしょうから、 保存則方程式を勉強したいと言えばさせてもらえるような気がしますので、 そういう先生を探してみるといいのではないかと思います。
最近は、大きな大学 (旧帝大、東工大、早稲田、慶應など) の数学科なら、 それぞれそういう分野の先生が少なくとも 1 人位はおられるような気がします。
またいっそ、保存則方程式の プレプリントサーバ に論文を投稿している研究者のいる海外の大学へ留学する、 なんていう方向もあるかもしれません。 実際、海外の先生のところで保存則を学んできた 日本の研究者も何人かおられます。
(04/01 2008 更新)QandA 2.5.にも書きましたが、 保存則方程式で不連続性を持つ解を衝撃波といいます。 気体の方程式の場合の物理現象の衝撃波に対応する解です。
衝撃波解は、ランキン−ユゴニオ条件、およびエントロピー条件と呼ばれる 条件を満たす必要があります。
(06/05 2001)初期値が
の形の、保存則方程式の初期値問題のことをいいます。 (06/05 2001)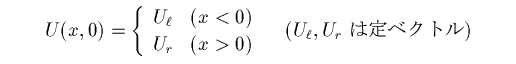
ええ、あの リーマン(G.F.B.Riemann 1826-1866 独) のようです。
流体力学も研究していたようで、他にも Riemann 不変量という 彼が導入した量に名前が残っています。詳しくは Courant Friedrichs の本をご覧下さい。
(06/05 2001; 12/23 2001 修正)幾つかの理由が考えられます。
Riemann 問題は 1957 年に Lax により一般的に解かれることが示されていて どのように解けばよいかもそれにより分かっています (例えば Smoller の本参照)。 それがどのような解であるか、少し簡単に説明します。
その解には、N 個の各特性方向に対応した波がその特性速度に従って 左から右へ順に現われ、波と波の間は定数状態 (両端を含めて (N+1) 個) になります。
各波は、その特性方向が真性非線形 (genuinely nonlinear) ならば 衝撃波 (shock wave)、または膨張波 (rarefaction wave) であり、 線形退化 (linearly degenerate) ならば接触不連続 (contact discontinuity) となります。 Riemann 問題の解の場合、衝撃波と接触不連続は一定速度で進む不連続な 断層の形の波、 膨張波は x/t の関数の形の自己相似的な連続波で、 いずれも簡単な式で書けます。
この波の左の定数状態を固定すると波の右に現われ得る定数状態は 任意ではなく、非線形な 1 パラメータの族を作り その 1 パラメータの族を表す式は具体的に書き下すことができます。 よってあとはそれらの族を使って (N-1) 個の定数状態 (と同等な N 個のパラメータ) を決定すればいいのですが、 それには N 本の連立非線形方程式 (微分方程式ではありません) を解く必要があり その解が一意であることは陰関数定理により示されているのですが、 残念ながらそれを具体的に書き下すことは、 ごく単純な方程式の場合を除いては簡単ではありません。
よって気体の方程式の Riemann 問題を数値計算する場合は (Godunov 型差分近似、乱数選択法などで必要となるようです) その非線形方程式の解を Newton 法等の近似計算法により求める、 といったことが行なわれることが多いようです。 詳しくは例えば Toro の本や LeVeque の本を参照して下さい。
(12/21 2001; 12/23 2001 修正)これは、「Q 3.4. 何故 Riemann 問題を考えるのですか」 に書いた、
方程式はスケール変換 (x,t) ==> (Ax,At) に関して不変であり、 それにより x/t の関数の形の自己相似解を持つことになる。に対する疑問だと思います。
確かに一般には非線形 (半線形、準線形) の方程式、 および変数係数の線形の方程式でも 特性曲線は直線ではなく曲線となります。 特性曲線が直線で話が済むのは、限られた方程式、 限られた問題だけです。 斉次の保存則方程式は、その限られた方程式の一つです。 非斉次、あるいは変数係数の保存則方程式だと そういう綺麗な性質が崩れて、数学的な解析も少し難しくなります。
この、保存則方程式と特性曲線の関係については、 「conservation law に関する document」 の、「非線形波動方程式入門」 を参考にしてみてください。 特性曲線について線形、半線形、準線形の方程式について 例を上げながら説明していて、 最後は単独保存則のリーマン問題の説明もしています。 連立の保存則方程式までは説明していませんが (いつか書こうかなとは思っています)、 それはこれを見た後で保存則方程式の成書 (例えば Smoller のテキスト など) を見られたらよいと思います。
(10/15 2005)QandA 2.3 で紹介した中の日本語の文献で言えば、 単独の方程式 (バーガース方程式) の Riemann 問題の話ならば 「非線形保存則系入門」 (吉川) にも 少し書かれていますし、「はじめての CFD」 (棚橋) にも (散発的にですが) 書かれています。 バーガース方程式の Riemann 問題ならば、 私の 「非線形波動方程式入門」 にも書かれています。
連立方程式の保存則系に対する Riemann 問題については、 2x2 の気体の方程式の場合に 「非線形の現象と解析」 (西田、川島) に書かれていますし、同様の方程式、 および一般の単独方程式の場合の Riemann 問題に関する話が 「非線形微分方程式の大域解」 (松村、西原) に書かれています。
しかし、そういえば一般の連立方程式の場合 (NxN) の Riemann 問題の話は 日本語の文献ではあまり見ませんね (結果だけなら 「双曲型保存則系の初期値問題」 (浅倉) にも簡単に触れられています)。
何でしたら、そのうちにそんな文章でも書きましょうか。
(11/06 2005)追加ですが、現在、「リーマン問題入門」 として そのようなものを書いて公開しています。 ただし、うだうだ書いたためにかなり長く、ちょっと読みにくいと思います。
(10/09 2007)超関数の意味での解、つまり弱形式での解とみた物です。詳しく述べると、 次のようになります。
U(x,t) が V(x) を初期値 (U(x,0)=V(x)) とする弱解であるとは、 (-∞,∞)×[0,∞) 上にコンパクトな台 (support) を持つ任意の連続微分可能な 実数値関数 φ(x,t) に対して
を満たすこと、をいいます。 部分積分で U,F(U) に対する微分を、テスト関数である φ の方に 持って行った、という形になっています。 これで微分可能でない U を解として考えることができるようになるわけです。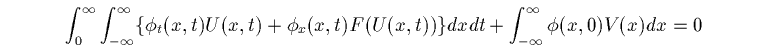
ただし、これにより今度は解のクラスが広くなり、解は存在しやすくなりますが、 一意性を示しにくくなります。
なお、上の定義のテスト関数 φ は、ベクトル値だと思って U, F(U), V との 積は内積だと思っても、 また、スカラー値だと思ってベクトルのスカラー倍だと思ってもどちらでも 結構です。φ の任意性によりそれらは同じことになります。
(06/05 2001; 03/16 2007 修正)不動点定理などが直接は使えないので、作りやすい近似解を作り、 その弱解への収束を示す、というのが普通のやり方です。
しかし、それも割と面倒で、今まで収束が示されている近似解には
なお、粘性近似解とは、人工粘性項をつけた放物型方程式
の解のことであり、Lax-Friedrichs 差分近似解とは、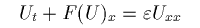
のような差分近似から作られる近似解のことをいいます。 他の近似解は簡単には説明できませんので、QandA 2.3 で 紹介した本や、または conservation law に関する論文などを参照して下さい。 (06/05 2001)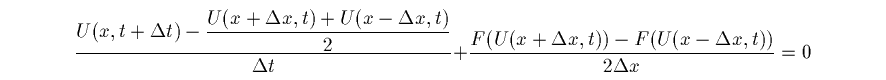
QandA 4.6も ご覧ください。
(07/21 2001)単独保存則方程式 (N=1) については、エントロピー条件を満たす弱解 (エントロピー解) の存在と一意性は証明されています (1957 Oleinik)。
しかし、連立の保存則方程式についてはエントロピー解の一意性は まだ完全には証明されていません。解のある程度の正則性 (区分的に滑らか などの滑らかさの条件) を仮定した場合の一意性が知られているのみです。
最近、Bressan により、Glimm 差分近似解の極限の一意性、あるいは Glimm 差分近似と波面追跡法の極限が一致することなど、 定数に近い状態の解の一意性が少しずつ明らかになってきています。
しかし、完全な形でのエントロピー解の一意性の証明にはまだかなり 時間を要するように思います。
(06/05 2001)適切性のためにはこれも必要なのですが、これも実はあまり 良く分かってはいません。
これに関しても最近 Bressan が定数に近い初期値に対しては 証明しています。 彼の方法は非常に強力で、今後も色んなことが明らかにされていくことでしょう。
(06/05 2001)一意性や初期値に関する連続依存性よりは色々なことが以前から知られています。
特に、気体力学で知られている N 型波と呼ばれる波への漸近減衰性は、 非線形により起こるものとして古くから研究され、その収束の速さなども 知られています。
その研究には、連立方程式の場合には、主に Glimm の差分近似解と 一般化特性曲線というものが使われるようです。
(06/05 2001)解の構成方法の大まかな話についてはQandA 4.2 を ご覧ください。それぞれについて文献を紹介します。
これに関しては、Smoller の本にも載っていますし、 論文であれば
これも Smoller の本に載っていますし、 日本語の記事もあります。
なお、Glimm の差分法は、"interaction estimate" という キーとなる定理があり、その証明が少しやっかいなのですが、 Serre の本の 1 の Lemma 5.8.1 に とても簡潔な証明が書かれています。
追加ですが、「Glimm 差分法解説」 なるものを書いてみました (2007 年 10 月)。
これは Bressan の本、 Holden, Risebro の本、 日本語の記事などが参考になると思います。 他にも以下のような物があります。
これは私の専門分野なのですが、これに関する文献については、 「conservation law に関する dcument」 の節にある 文献の一覧表 をご覧ください。 やや古くなったかも知れませんがそう大きな変化はないと思います (^^;
ただ、連立方程式に関しては DiPerna にしろ、Serre にしろ、 Ding, Chen, Luo にしろ、いずれもかなり面倒です。 Smoller や Hoermander の本にも少し触れられていますから それで概観を知るというのも手でしょうし、 Tartar の原論文で単独保存則方程式について概要を知るのもいいでしょう。
なお、Tartar の単独保存則方程式に関する方法 (を Chen, Lu が改良したもの) を話す機会があり、 それを日本語でまとめたもの (cf. 「 compensated compactness と保存則方程式について」) が数理研講究録に掲載されました。
また、最近補完測度法に関する Lu Yunguang の本 も出版されました。
難しいものは難しいと思います。それには幾つかの理由があります。
確かに私が使っている Lax-Friedrichs の差分近似解は 1 次近似でしかなく、 解をなまらせる効果 (粘性効果) が強いものとして知られていて、 通常数値計算の分野ではより良い近似法が色々と使われています。
私が Lax-Friedrichs の差分を使っているのには少し理由があります。
「Q 1.3 そのあなたはどんなことを研究しているのですか」でも 述べましたが、 私が主に使っているのは補完測度法 (compensated compactness theory; 補償コンパクト性理論とも呼ばれる) と呼ばれる近似解の収束証明法なのですが、 それはどんな近似解の収束も示すことができる訳ではなく、 今の所 Lax-Friedrichs 差分近似や人工粘性法などの粘性の強い近似解や 緩和法 (relaxation) などの列にしか適用されておらず、 例えば存在証明で良く使われる Glimm の差分法や、数値解析でよく用いられる 2 次精度の Lax-Wendroff 法などの近似解列には適用されません。
それは近似解が持つ一様な性質が違うからだと思っています。 そして、私が調べているのは、
近似解が一様にある性質を持つことを証明することで その近似解の極限 (補完測度法により存在が示される極限) としての 弱解がその性質を満たすことを示すという方法で、それに数値計算を使っています。 よって、もし単に
「極限としての弱解がそのような性質を持つことを数値計算で検証する」ということを調べたいなら精度の良い計算法を使えば良いのですが、 私の場合にはこれではだめで、
「そのような性質を補完測度法で収束が保証されている近似解が、 一様に (近似的に) 満たす」ということを確認する必要があります。
Lax-Wendroff 程度ならばさほど計算の手間は変わらないのですが、 Godunov や他の手法では Riemann-solver (Riemann 問題の解の数値計算) とか、面倒な数値計算を行なわなければいけません。
元々数値シミュレーションが目的でなく、 性質の予想をたてる、あるいは検証する程度なので ある程度はいい加減に考えています (^^;
ただ、確かに粘性効果が強いとそれにかくれてしまう性質もあり、 精度が良いに越したことはないので、 一応 Lax-Friedrichs でも分割数を変えたデータ同士で比較してみるとか、 2 次精度の近似解と比較してみるとか、 その辺りの検証も多少は行なっています。
確かに、人工粘性を使っている論文等では、 「標準的なやり方でそのような近似解の存在は容易に証明できる」 と書かれていることが多いようです。
基本的には、人工粘性方程式は半線形熱方程式になるので、 確かにその半線形熱方程式に関する「標準的なやり方」で近似解は作れますが、 時間大域解を作るときに a priori 評価と呼ばれるものが 少し面倒になることがあります。
例えば、「非線形微分方程式の大域解」 (松村、西原) の第 2 章に、 単独保存則方程式である Burgers 方程式に粘性がついたもの (数式は Q 2.2 の 式 を参照) の大域解の存在証明が書かれています。 連立方程式の場合も、これを元に考えてみるといいでしょう。
ただ、例えば Euler 座標系での等エントロピー流 (数式は Q 2.2 の 式 を参照) などの場合、密度ρの下からの評価が必要になります。 この場合の人工粘性近似解の大域解の存在については、 DiPerna のこの方程式に対する補間測度法に関する原論文:
何でしたら、そのうちにそんな文章でも書きましょうか。
(03/17 2006)まず「エントロピー」と「エントロピー条件」について説明します。
保存則方程式
Ut+F(U)x=0 (U=U(t,x)∈RN、t>0、x∈R、F:RN→RN)に対して、RN から R への関数 η(U)、q(U) が、
∇q(U)=∇η(U)∇F(U)を満たすとき、 すなわち、保存則方程式の「滑らかな」解 U=U(t,x) に対して追加保存則
η(U)t+q(U)x=0を満たすとき、 保存則方程式ではη(U)、q(U) を エントロピー対 と呼び、 η(U) を (一般化された) エントロピー ((generalized) entropy)、 q(U) を エントロピー流束 (entropy flux) と呼びます。
これは、もちろん気体の方程式の場合の物理的なエントロピー S に 対応して名付けられたものです。実際、S は Euler 座標系では、 次のような追加保存則を満たします (ρは気体密度、u は気体速度):
(ρS)t+(ρSu)x=0つまり、この場合はη=ρS、q=ρSu なわけです。
そして、保存則方程式の弱解 U=U(t,x) は、 次の「エントロピー条件」を満たす必要があります:
η(U)t+q(U)x≦ 0 (超関数の意味で)ここで、η(U)、q(U) は、η(U) が U に関して凸関数であるような 任意のエントロピー対です。
このエントロピー条件は、 確かに「(一般化) エントロピーη(U) が減少する」ような不等式になっていて、 通常の物理学での熱力学の法則である「エントロピーは増大する」ということとは 逆になってしまっています。
これは、エントロピー条件の定義を「凸な (一般化) エントロピーに対して」 としているために起きていて、 上に書いた気体の方程式の場合のエントロピー ρS は 実は「凹な (一般化) エントロピー」になっています。 よって、エントロピー条件に現れる (一般化) エントロピーη(U) は、 S に対しては η=-ρS とすべきものなわけです。
すなわち、確かに「(一般化) エントロピーは減少する」という形のものが 数学的なエントロピー条件なのですが、 それは物理的に不整合というわけではなくて、 「(一般化) エントロピーの定義に物理的なエントロピーの (-1) 倍がついている」 という事情によるわけです。 よって、物理的には問題なく整合しています。
このようなことになってしまったのは、 多分この (一般化) エントロピーを以下の論文で最初に深く考察した Lax が 「凸なエントロピー」に対する、 上の向きの不等号のエントロピー条件の研究を行っているからでしょう:
しかしこの論文で Lax は、エントロピー条件という言葉は使っているものの、 η(U) を「エントロピー」とは呼んではいないので、 むしろη(U) を「エントロピー」と呼ぶようにした人に責任があるのかもしれません (残念ながら誰であるかはちょっとわかりません)。
(06/11 2009; 06/12 2009 修正)新しく出た、保存則方程式に関する本などは、 「Q and A」 の 「Q 2.3. conservation law を勉強するには」 「Q 4.6. 弱解の構成方法を勉強したいのですが」 辺りに追加して行きますのでそちらを参照して下さい。
