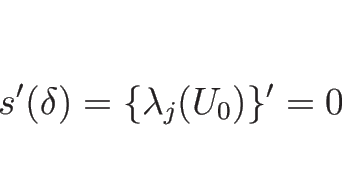B.2 数学的な一般化エントロピー
前節で物理的なエントロピー 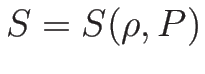 を
(B.3) として導いたが、
今度はこれと方程式 (3.12) との
数学的な関係を見てみる。
を
(B.3) として導いたが、
今度はこれと方程式 (3.12) との
数学的な関係を見てみる。
この方程式 (3.12) の滑らかな解に対しては、
(3.14) より、
となるので、よって
が成り立つ。
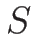 は単位質量あたりのエントロピーなので、全質量に対するエントロピー
は単位質量あたりのエントロピーなので、全質量に対するエントロピー
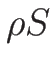 を考えると、
を考えると、
となるので、
となることがわかる。
このように、一般に保存則方程式
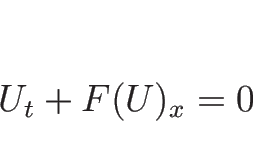 |
(B.124) |
の滑らかな解に対して、必ず
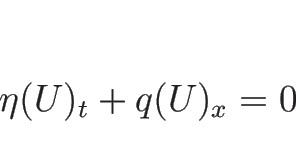 |
(B.125) |
となるスカラー関数 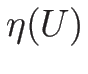 ,
, 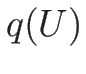 が存在する場合、
これを (一般化された) エントロピー対 (generalized entropy pair)
と呼び、
が存在する場合、
これを (一般化された) エントロピー対 (generalized entropy pair)
と呼び、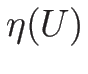 を エントロピー関数 (entropy)、
を エントロピー関数 (entropy)、
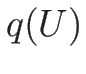 を エントロピー流束 (entropy flux) と呼ぶ。
を エントロピー流束 (entropy flux) と呼ぶ。
式 (B.5) は
と書けるので、(B.4) より
となる。よって、
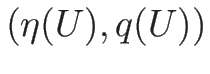 がエントロピー対となることは、
がエントロピー対となることは、
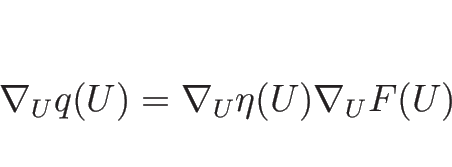 |
(B.126) |
が成り立つことを意味する。
しかし、(B.5) は衝撃波では成立しない。
それを調べるために、
不連続線での 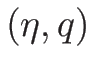 に対するランキン-ユゴニオ条件のような式
に対するランキン-ユゴニオ条件のような式
を調べてみる。
ここで、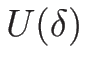 は、
衝撃波曲線 (4.7 節)、
または接触不連続曲線 (4.6 節)
を表し、
は、
衝撃波曲線 (4.7 節)、
または接触不連続曲線 (4.6 節)
を表し、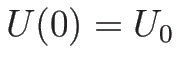 ,
,
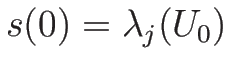 であるとする。
であるとする。
(B.6) より、
となるが、ランキン-ユゴニオ条件
を微分すれば、
なので、
![\begin{displaymath}
\frac{d \Phi}{d \delta}
=s'[\eta]-s'\nabla_U\eta(U)[U]
=-s'\{\eta(U_0)-\eta(U)-\nabla_U\eta(U)(U_0-U)\}\end{displaymath}](img1379.png) |
(B.127) |
となる。今、
とすれば、
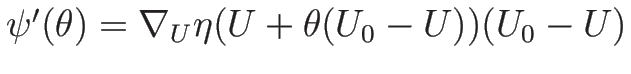 より、
(B.7) の中かっこ内は、
より、
(B.7) の中かっこ内は、
と書ける。
今、
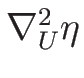 を、
を、 成分が
成分が
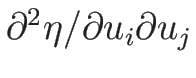 である
である 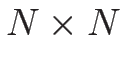 行列
であるとすると、
行列
であるとすると、
であるので、
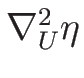 が正定値 (つまり
が正定値 (つまり 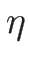 が凸) であれば、
(B.7) の中かっこ内は正となる。
ここで、
が凸) であれば、
(B.7) の中かっこ内は正となる。
ここで、
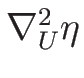 が正定値であるとは、
任意のベクトル
が正定値であるとは、
任意のベクトル 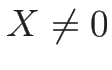 に対して、
2 次形式
に対して、
2 次形式
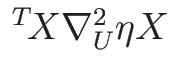 が正であることを意味する。
が正であることを意味する。
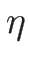 が凹 (
が凹 (
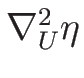 が負定値) ならば逆に
(B.7) の中かっこは負となる。
が負定値) ならば逆に
(B.7) の中かっこは負となる。
また、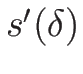 は、衝撃波の場合は
は、衝撃波の場合は
であったから、
少なくとも 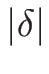 が十分小さければ
が十分小さければ 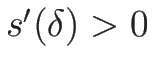 となる。
となる。
よって衝撃波の場合は、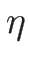 が凸ならば
が凸ならば 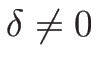 のときは
のときは
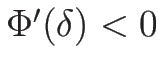 となり、
となり、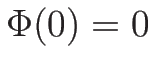 より、
より、
となる。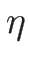 が凹ならば、逆に
が凹ならば、逆に
となる。
つまり、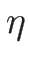 が凸か凹ならば、
が凸か凹ならば、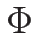 は衝撃波に対しては
どこでも一定符号であることになる。
後で示すように
(B.4 節参照)、
は衝撃波に対しては
どこでも一定符号であることになる。
後で示すように
(B.4 節参照)、
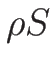 は
は
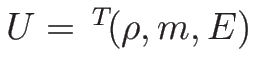 に関して凹となるので、
それが言える。
に関して凹となるので、
それが言える。
一方、接触不連続に対しては、
なので、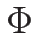 は 0 である。
よって、
は 0 である。
よって、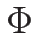 の符号を指定すること
(例えば凸なエントロピーに対して
の符号を指定すること
(例えば凸なエントロピーに対して 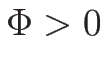 のような条件) によって、
適切な衝撃波のみを選択できることがわかる。
のような条件) によって、
適切な衝撃波のみを選択できることがわかる。
竹野茂治@新潟工科大学
2018-08-01
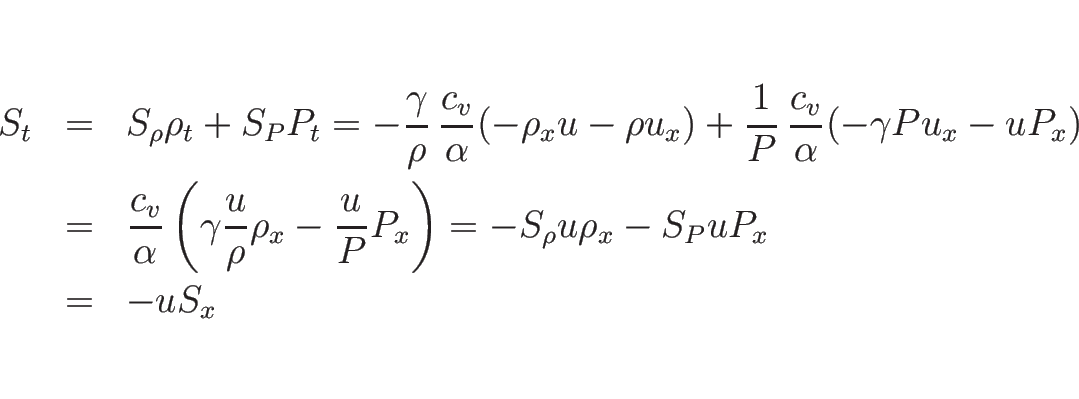
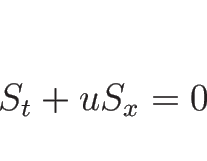
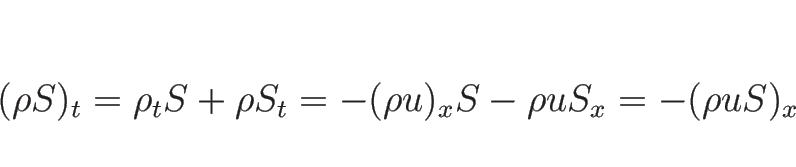
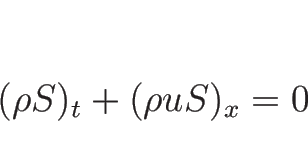
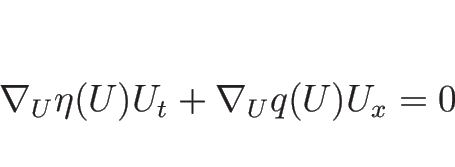
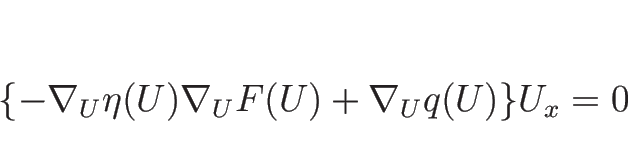
![]() に対するランキン-ユゴニオ条件のような式
に対するランキン-ユゴニオ条件のような式
![\begin{displaymath}
\Phi=s[\eta]-[q]
=s(\delta)\{\eta(U(\delta))-\eta(U_0)\}
-\{q(U(\delta))-q(U_0)\}
\end{displaymath}](img1372.png)
![\begin{eqnarray*}\frac{d \Phi}{d \delta}
&=&
s'[\eta]+s\eta'-q'
=
s'[\eta]+s...
...la_Uq(U)U'
\\ &=&
s'[\eta]+\nabla_U\eta(U)\{s-\nabla_UF(U)\}U' \end{eqnarray*}](img1376.png)
![\begin{displaymath}
s[U]-[F]
=s(\delta)\{U(\delta)-U_0\}-\{F(U(\delta))-F(U_0)\}
=0
\end{displaymath}](img1377.png)
![\begin{displaymath}
s'[U]+sU'-F'
=s'[U]+\{s-\nabla_UF(U)\}U'
=0
\end{displaymath}](img1378.png)
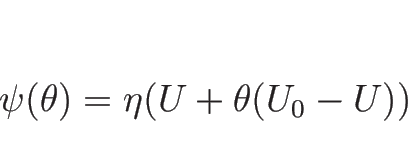
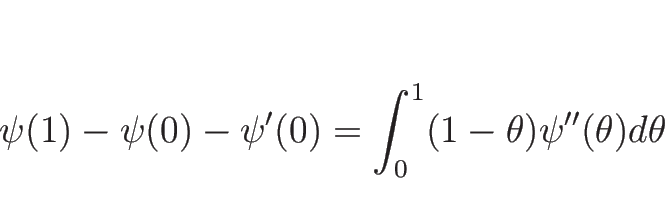
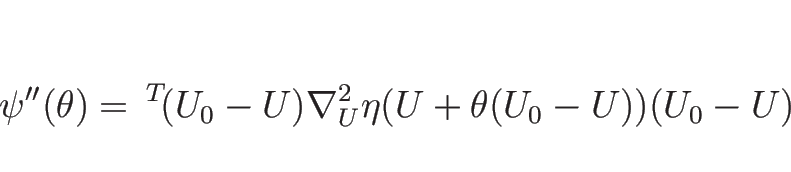
![]() は、衝撃波の場合は
は、衝撃波の場合は
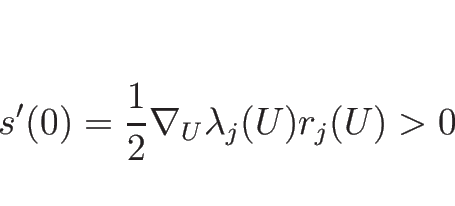
![]() が凸ならば
が凸ならば ![]() のときは
のときは
![]() となり、
となり、![]() より、
より、
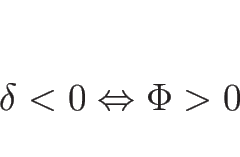
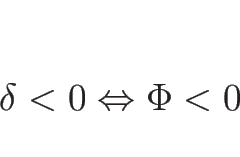
![]() が凸か凹ならば、
が凸か凹ならば、![]() は衝撃波に対しては
どこでも一定符号であることになる。
後で示すように
(B.4 節参照)、
は衝撃波に対しては
どこでも一定符号であることになる。
後で示すように
(B.4 節参照)、
![]() は
は
![]() に関して凹となるので、
それが言える。
に関して凹となるので、
それが言える。