(4.35) より、この場合は ![]() であるから、
であるから、
![]() と
と ![]() の間には次のような関係があることがわかる。
の間には次のような関係があることがわかる。
![]() が十分小さければ、
が十分小さければ、
![]() は次を満たす
(
は次を満たす
(
![]() とする):
とする):
証明
まず、
![]() より、
より、
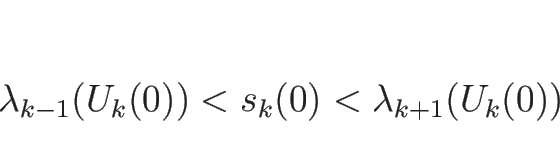
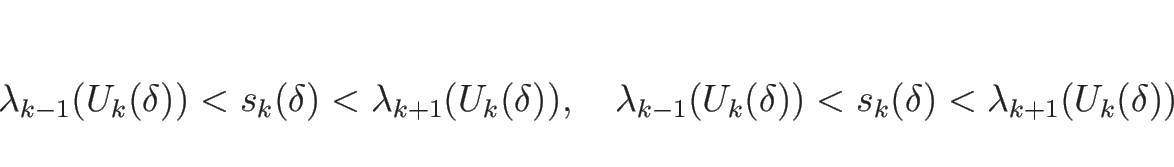
また、![]() であるので、
であるので、![]() が十分小さければ、
が十分小さければ、
![]() のとき、
のとき、
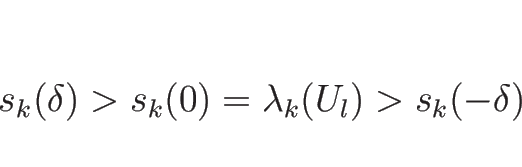
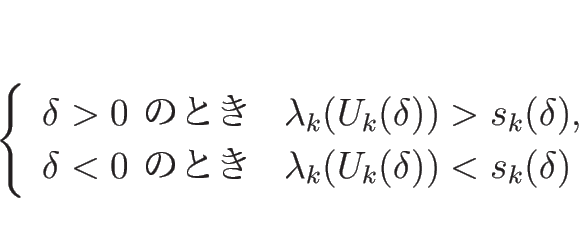
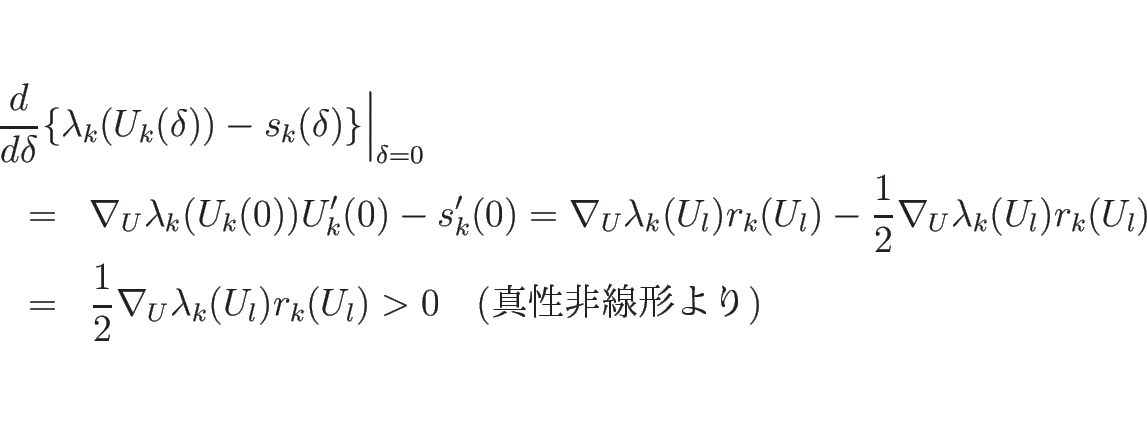
ところが、この ![]() の不連続解は、
後で見るように解の一意性も保証しないし、
理想気体の場合には膨張する (圧力が不連続線の通過にともなって減少する)
不連続解になっていて、
エントロピーも減少させるものであることが知られているので、
物理的には受け入れられないものである。
の不連続解は、
後で見るように解の一意性も保証しないし、
理想気体の場合には膨張する (圧力が不連続線の通過にともなって減少する)
不連続解になっていて、
エントロピーも減少させるものであることが知られているので、
物理的には受け入れられないものである。
よって、真性非線形の場合は不連続解のうち、
条件 (4.41) を満たすもののみを解として
採用することとする。この条件 (4.41) を
ラックス条件 (Lax's condition) または
ラックスのエントロピー条件 と呼び、
これを満たす不連続解を ![]() -衝撃波 (
-衝撃波 (![]() -shock wave)、
相空間上の曲線
-shock wave)、
相空間上の曲線 ![]() (
(![]() ) を
) を
![]() -衝撃波曲線 (
-衝撃波曲線 (![]() -shock curve,
-shock curve, ![]() -shock wave curve) と呼ぶ。
-shock wave curve) と呼ぶ。
なお、ここでは排除した ![]() の場合の不連続解も全く無益なわけではなく、
例えば最近保存則系方程式の研究で有益な手段である波面追跡法では、
膨張波の近似にこの
の場合の不連続解も全く無益なわけではなく、
例えば最近保存則系方程式の研究で有益な手段である波面追跡法では、
膨張波の近似にこの ![]() の不連続解 (膨張的衝撃波とも呼ばれる)
が利用される。
の不連続解 (膨張的衝撃波とも呼ばれる)
が利用される。
竹野茂治@新潟工科大学