![\begin{eqnarray*}0
&=&
-\int_a^b\eta(U(t_0,x))dx+\int_{X_1}^{X_2}\eta(U(t_1,x...
...gr]_{X(t;t_0,a)}^{X(t;t_0,b)}dt
\\ &&
+\int_{t_0}^{t_1}\Phi dt\end{eqnarray*}](img1401.png)
![\begin{eqnarray*}0
&=&
-\int_a^b\eta(U(t_0,x))dx+\int_{X_1}^{X_2}\eta(U(t_1,x...
...gr]_{X(t;t_0,a)}^{X(t;t_0,b)}dt
\\ &&
+\int_{t_0}^{t_1}\Phi dt\end{eqnarray*}](img1401.png)
ここからの類推として、弱解にも同様の条件、
すなわち凸なエントロピーに対して
「エントロピーの総量が減少していること」
を課すのがエントロピー条件である
(![]() は凹なので、
は凹なので、![]() とは逆になることに注意)。
とは逆になることに注意)。
しかし、一般の ![]() の関数に対して、線積分
の関数に対して、線積分
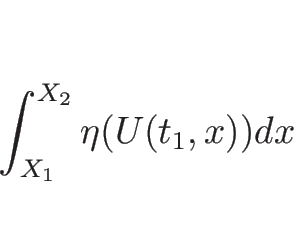
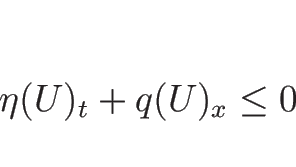
「凸なエントロピー関数を持つ任意のエントロピー対と 任意の非負なテスト関数に対して
を満たすこと」を、エントロピー条件 (entropy condition) と呼ぶ。
保存則の一般的な解の存在定理では、
通常ラックス条件の代わりにこの条件が用いられる。
この形の条件であれば、単純な不連続性の関数でなく、
もっと一般の ![]() の関数に対して適用できる。
の関数に対して適用できる。
以下に、簡単な場合についてこの条件を考えてみる。
解 ![]() が滑らかな部分では、
が滑らかな部分では、![]() となるので、
もちろんエントロピー条件は満たされる。
となるので、
もちろんエントロピー条件は満たされる。
![]() が不連続線
が不連続線 ![]() の両側で滑らかな場合は、
条件 (B.9) は、
A 節の図 A.3 のように分けて計算すれば、
の両側で滑らかな場合は、
条件 (B.9) は、
A 節の図 A.3 のように分けて計算すれば、
![\begin{eqnarray*}0
&\leq &
\int\!\!\!\int _Q\{\eta(U)\phi_t+q(U)\phi_x\}dxdt
...
...q\phi dt)
\\ &=&
\int_{x=d(t)}\phi(t,d(t))\{[\eta]d'(t)-[q]\}dt\end{eqnarray*}](img1412.png)
竹野茂治@新潟工科大学