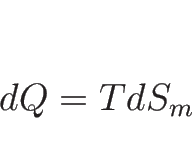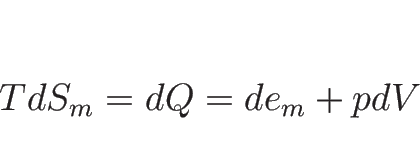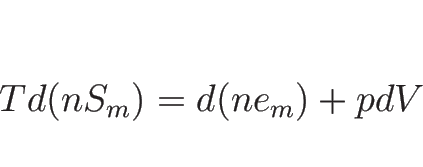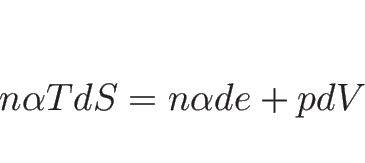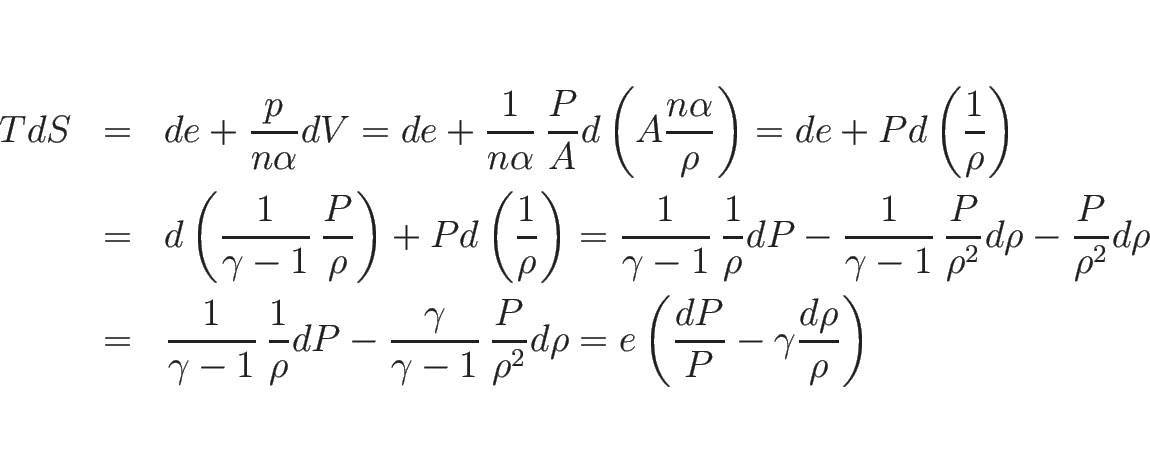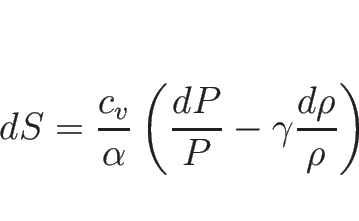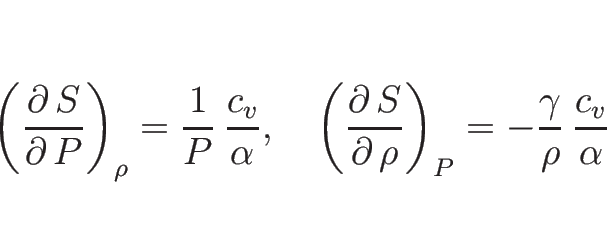B.1 理想気体に対するエントロピー
次は、A 節の最後で述べたように、
一般の弱解に対して物理的に意味のある解を選別するための、
ラックス条件に代わるエントロピー条件についてここで説明する。
まず、具体的なエントロピーについて紹介し、
その後で数学的なエントロピーとエントロピー条件について説明することにする。
2 節で考察した理想気体では、
よく知られているように定常状態の気体に対して状態方程式
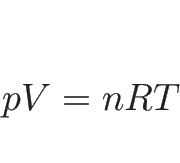 |
(B.121) |
が成り立つとする。
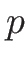 は単位面積あたりの気体の圧力、
は単位面積あたりの気体の圧力、
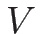 は気体の体積、
は気体の体積、
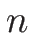 は気体のモル数、
は気体のモル数、
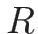 は気体の種類などにはよらない定数 (気体定数)、
は気体の種類などにはよらない定数 (気体定数)、
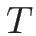 は絶対温度である。
は絶対温度である。
2 節の記号で書くと、
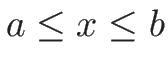 の範囲の定常的な気体で考えれば、
の範囲の定常的な気体で考えれば、
となるが、この部分の気体の質量は、
に等しい。よって、
と書けるので、これらを (B.1) に代入すれば
が得られる。
また、気体の 1 モルあたりの内部エネルギー 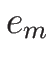 は、
理想的な場合には
は、
理想的な場合には 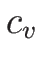 を定数 (定積モル比熱)として
を定数 (定積モル比熱)として
と書けることが知られている。
これに対し、2.5 節の 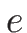 は
単位質量あたりの内部エネルギーなので、
は
単位質量あたりの内部エネルギーなので、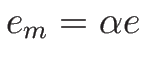 であり、
よって、
であり、
よって、
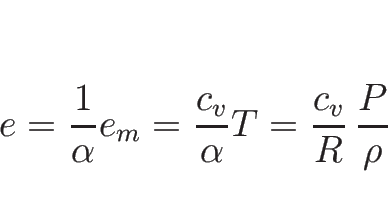 |
(B.122) |
となる。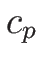 を低圧モル比熱、
を低圧モル比熱、
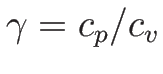 (比熱比) とすると、
(比熱比) とすると、
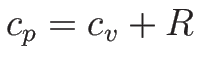 という関係 (マイヤーの関係) が成り立つことが知られていて、
よって、
という関係 (マイヤーの関係) が成り立つことが知られていて、
よって、
となり、(B.2) より
が得られる。これが (2.17) である。
さて、エントロピーは、1 モルあたりの気体の熱量 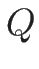 に対して
に対して
なるものとして定義される。
ここで 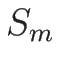 は気体の 1 モルあたりのエントロピーである。
は気体の 1 モルあたりのエントロピーである。
熱力学の第 1 法則により、1 モルの気体に対して
が成り立つ。
今、単位質量あたりのエントロピーを 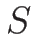 とすれば
とすれば 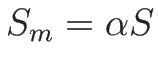 であり、
であり、
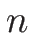 モルの気体に対する熱量変化を書けば、
モルの気体に対する熱量変化を書けば、
であり、よって、
となるので、
となる。
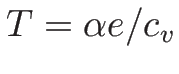 より、この両辺を
より、この両辺を 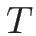 で割れば、
で割れば、
が得られる。よって、これを積分すれば
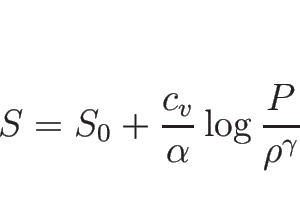 |
(B.123) |
と表される。また、
であることがわかる。
竹野茂治@新潟工科大学
2018-08-01
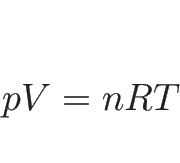
![]() の範囲の定常的な気体で考えれば、
の範囲の定常的な気体で考えれば、
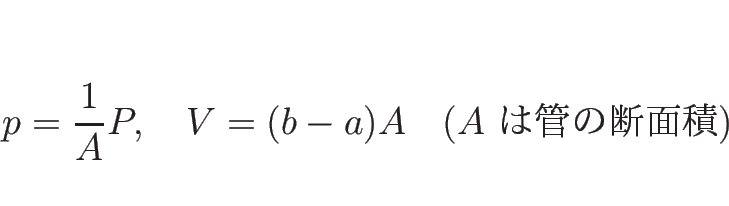
![\begin{displaymath}
M^1_{[a,b]}=(b-a)\rho=n\alpha
\hspace{1zw}(\mbox{$\alpha$\ はこの気体の (平均) 分子量})
\end{displaymath}](img1333.png)
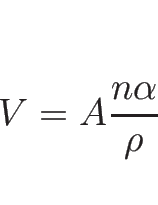
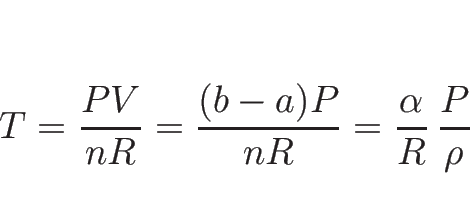
![]() は、
理想的な場合には
は、
理想的な場合には ![]() を定数 (定積モル比熱)として
を定数 (定積モル比熱)として
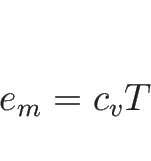
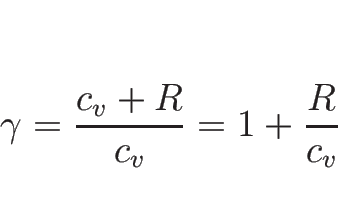
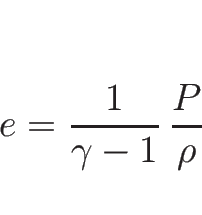
![]() に対して
に対して