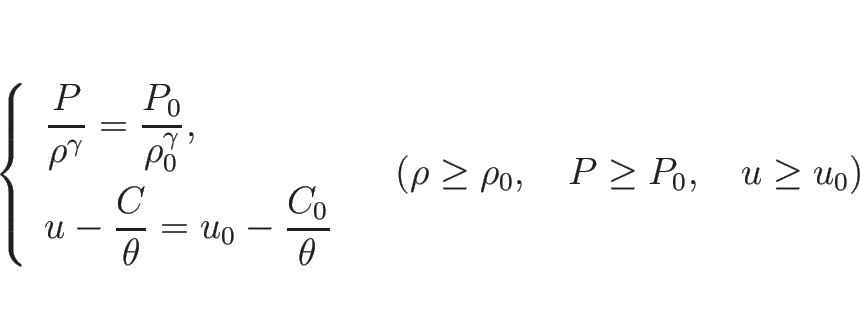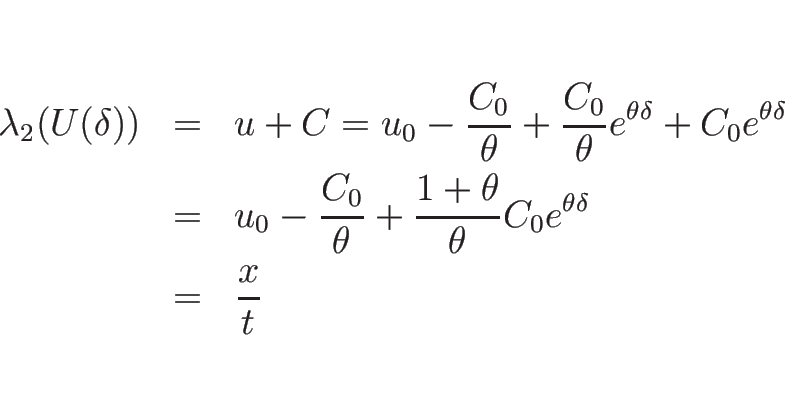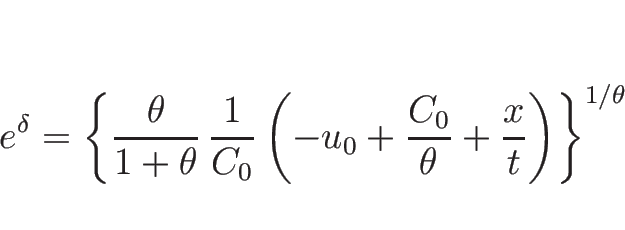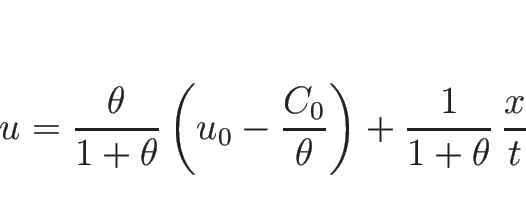3.5 オイラー座標系の理想気体の場合の例
ここでは、2.4, 2.5 節で紹介した、
オイラー座標系での理想気体の保存則方程式系 (2.10), (2.15), (2.16)
に対する固有値、固有ベクトル、リーマン不変量、膨張波解を計算する。
まず、
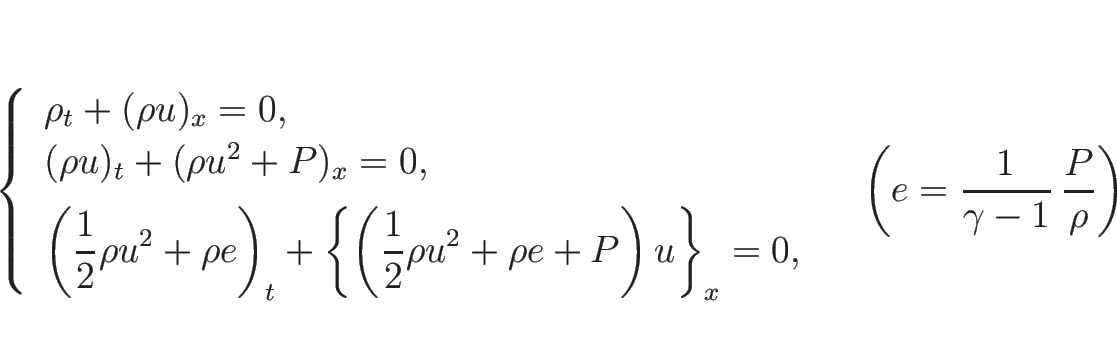 |
(3.31) |
を扱うが、そのために 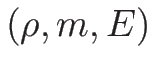 で考えても、
で考えても、
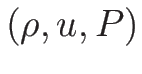 で考えても、それらには本質的な違いはないことを
まず示す。
で考えても、それらには本質的な違いはないことを
まず示す。
命題 3.2
準線形方程式系 (3.3) が
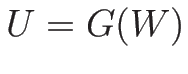 (
(
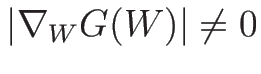 ) によって
) によって
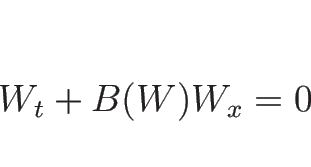 |
(3.32) |
と変換されるとき、(3.13) に
対する固有値 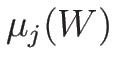 , 左右の固有ベクトル
, 左右の固有ベクトル
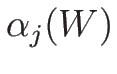 ,
, 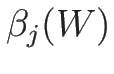 ,
, 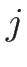 -リーマン不変量
-リーマン不変量 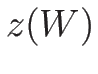 は、
以下のように得られる:
は、
以下のように得られる:
また、
が成り立ち、よって線形退化性、真性非線形性もこの変換で不変である。
証明
(3.3) に 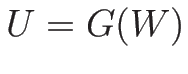 を代入すると
を代入すると
より、(3.13) の 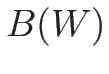 は
は
となる。よって 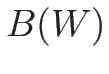 の固有値は
の固有値は
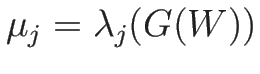 であり、
固有ベクトルは
であり、
固有ベクトルは
より、
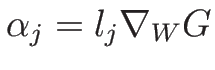 ,
,
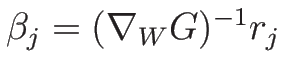 となる。
となる。
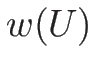 を (3.3) の
を (3.3) の
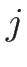 -リーマン不変量とし、
-リーマン不変量とし、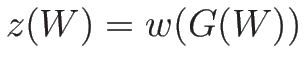 とすると、
とすると、
となるので、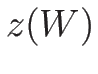 が
が 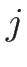 -リーマン不変量となる。
また、
-リーマン不変量となる。
また、
となるので、
(3.3) と (3.13)
の線形退化性、真性非線形性も変わらない。
この命題 3.2 より、
(3.12) を 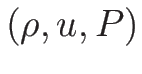 の式に直して考えてもよい
ので、それで考える。
(3.12) の第 1 式、第 2 式より、
の式に直して考えてもよい
ので、それで考える。
(3.12) の第 1 式、第 2 式より、
となるので 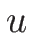 に関する方程式は
に関する方程式は
となる。第 3 式は
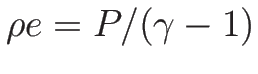 より、
より、
となるので、結局
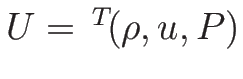 の方程式
の方程式
![\begin{displaymath}
\left[\begin{array}{c}\rho\\ u\\ P\end{array}\right]_t
+\l...
...ht]
\left[\begin{array}{c}\rho\\ u\\ P\end{array}\right]_x
=0\end{displaymath}](img339.png) |
(3.33) |
が得られる。この場合、 は
は
となる。
より、固有値は
固有ベクトルは
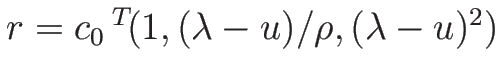 と
とればよいので、
と
とればよいので、
となる (これらは命題 3.2 の 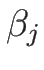 にあたる)。
にあたる)。
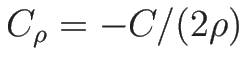 ,
, 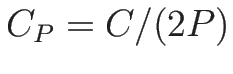 なので、
なので、
となり、
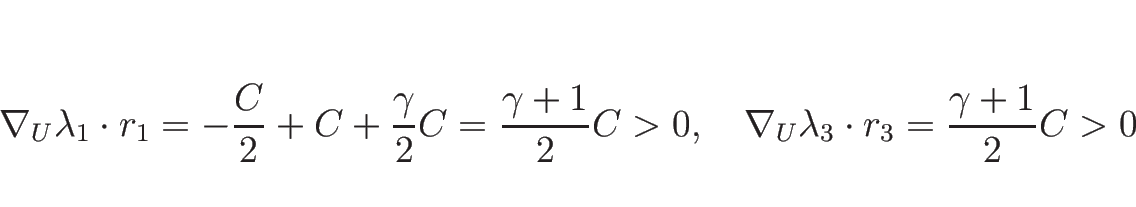 |
(3.34) |
となるので 1-特性方向、3-特性方向は真性非線形である。
一方、
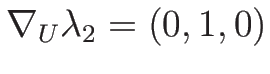 より
より
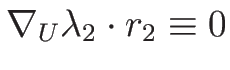 であるので、2-特性方向は線形退化となる。
よって、2-特性方向には膨張波解は存在しない。
であるので、2-特性方向は線形退化となる。
よって、2-特性方向には膨張波解は存在しない。
次にリーマン不変量を求める。
1-リーマン不変量は、
となるので、微分方程式 (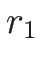 の積分曲線を与える方程式)
の積分曲線を与える方程式)
![\begin{displaymath}
\begin{array}{l}
\displaystyle \frac{d \rho}{d s}=\rho,\hs...
... P,\\ [.5zh]
(\rho(0),u(0),P(0))=(\rho_0,u_0,P_0)
\end{array}\end{displaymath}](img354.png) |
(3.35) |
を解くと、
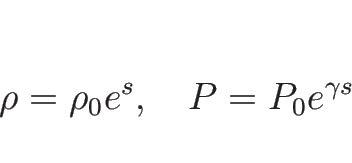 |
(3.36) |
となる。よって、
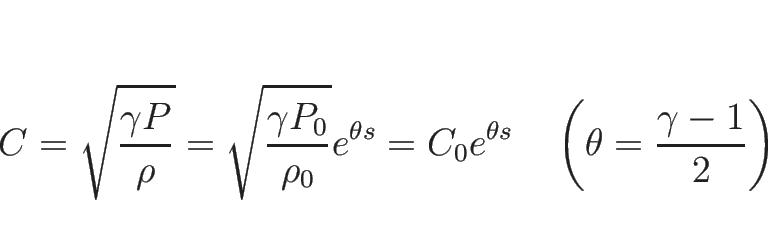 |
(3.37) |
より
となるので、よって
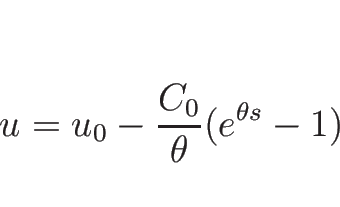 |
(3.38) |
となる。
Rimann 不変量はこの積分曲線 (3.17), (3.19) 上不変で
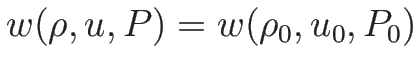 となるものだから、
(3.17) で
となるものだから、
(3.17) で 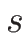 を消去すると、
を消去すると、
より、
となるので、
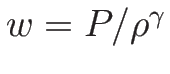 が一つの 1-リーマン不変量である。
が一つの 1-リーマン不変量である。
また、(3.18), (3.19) より
となるので、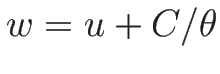 がもうひとつの 1-リーマン不変量となる。
がもうひとつの 1-リーマン不変量となる。
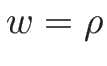 とすると、
とすると、
であるから、この 2 つのリーマン不変量に 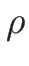 を加えると、
この
を加えると、
この
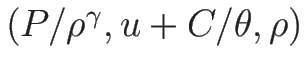 は相空間
は相空間  上で
上で
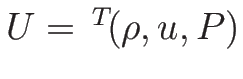 は 1 対 1 に対応する。
は 1 対 1 に対応する。
同様に、3-リーマン不変量の場合は、
(3.17) と
とより、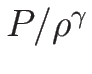 と
と 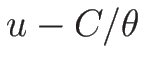 が 3-リーマン不変量であり、
が 3-リーマン不変量であり、
なので、
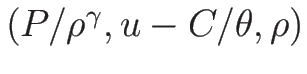 と
と 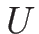 は 1 対 1 に対応する。
は 1 対 1 に対応する。
2-リーマン不変量は、
より、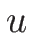 ,
, 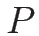 が 2-リーマン不変量であり、
同様に
が 2-リーマン不変量であり、
同様に 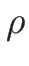 をつけ加えると
をつけ加えると 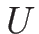 と 1 対 1 に対応する
(この場合は
と 1 対 1 に対応する
(この場合は 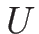 自身になる)。
自身になる)。
1-膨張波曲線 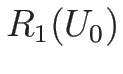 は、
は、
を満たしながら
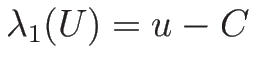 の増加方向に進む。
(3.16) より、
の増加方向に進む。
(3.16) より、
となるので、 の減少する方向が
の減少する方向が 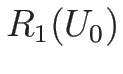 の伸びる方向。
よって、
の伸びる方向。
よって、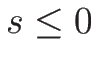 で、
で、
となるので、結局 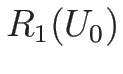 は、
は、
またはパラメータ表示により、
![\begin{displaymath}
\left\{\begin{array}{l}
\rho=\rho_0e^s,\\ [.5zh]
\display...
...h]
P=P_0e^{\gamma s}
\end{array}\right. \hspace{1zw}(s\leq 0)\end{displaymath}](img380.png) |
(3.39) |
と表される。
ここで、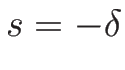 とすれば
とすれば 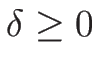 で、丁度
で、丁度
となる。
また、1-膨張波 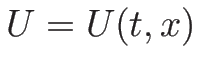 は、(3.8) より
は、(3.8) より
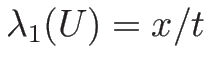 を満たす必要があるので、
を満たす必要があるので、
 によるパラメータ表示の式を代入すれば、
によるパラメータ表示の式を代入すれば、
となるので、
より
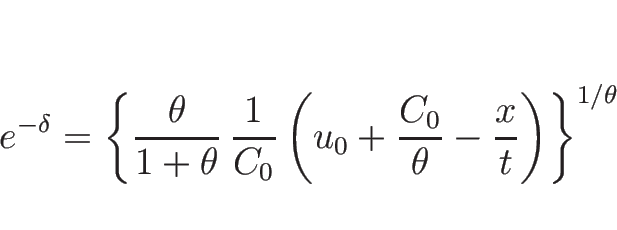 |
(3.40) |
となる。これを、(3.20) (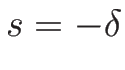 ) に代入すれば、
1-膨張波解を
) に代入すれば、
1-膨張波解を 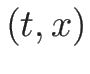 の式で表すことができることになる。
容易にわかる通り、
の式で表すことができることになる。
容易にわかる通り、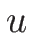 は
は 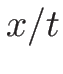 の一次式になる。より詳しく見れば、
の一次式になる。より詳しく見れば、
のようになる。
図 3.4:
ある 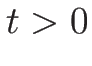 に対する膨張波解のグラフ
に対する膨張波解のグラフ
|
|
同様にして、3-膨張波曲線 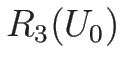 は、
は、
またはパラメータ表示により
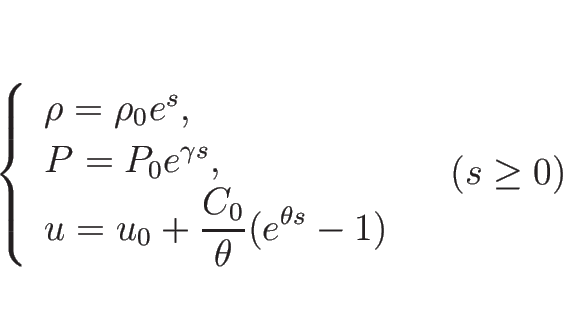 |
(3.41) |
と表される。
こちらは、 (
( )
でそのまま
)
でそのまま
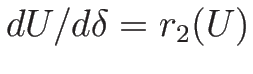 となり、
となり、
となるので、
を (3.22) ( ) に代入すれば 3-膨張波を
) に代入すれば 3-膨張波を 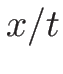 で表せる。
この場合も
で表せる。
この場合も 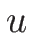 は
は 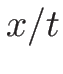 の一次式であり、
の一次式であり、
となる。
竹野茂治@新潟工科大学
2018-08-01
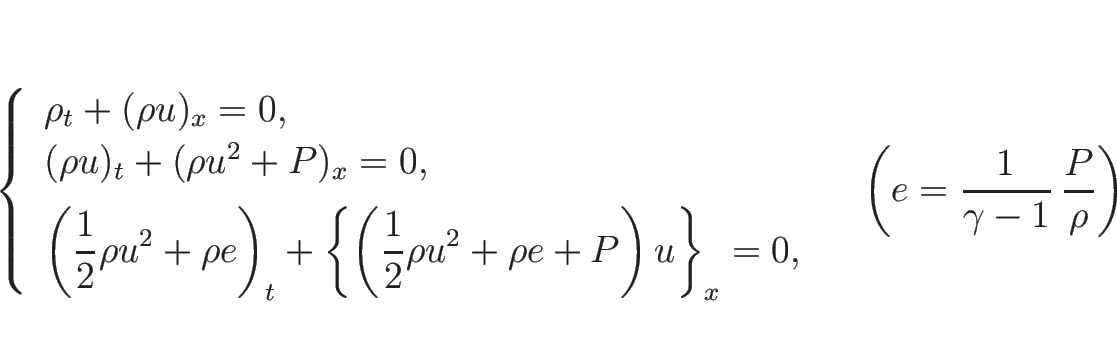
![]() (
(
![]() ) によって
) によって
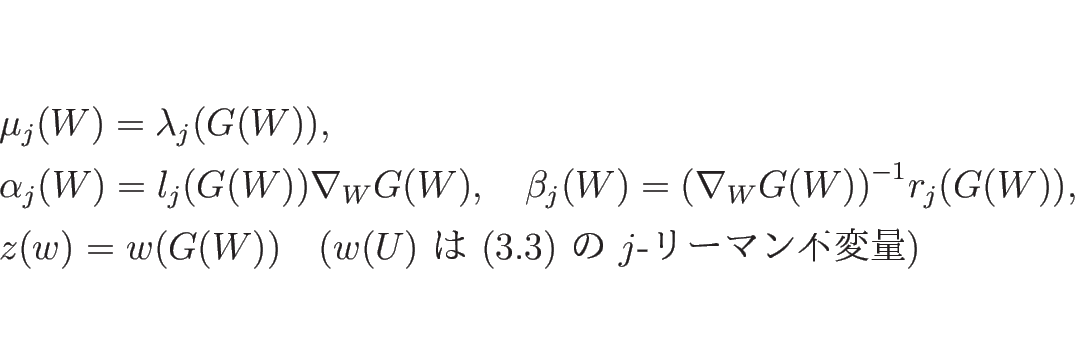
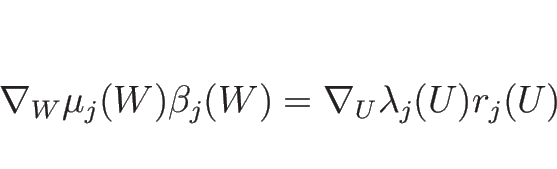
![]() を代入すると
を代入すると
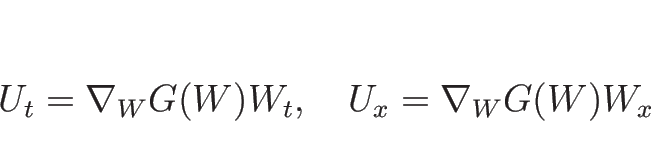
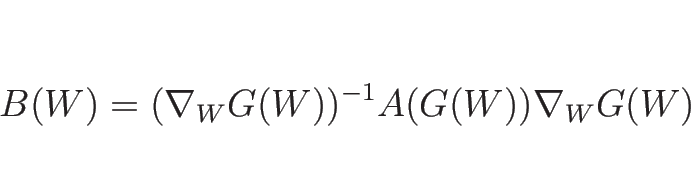
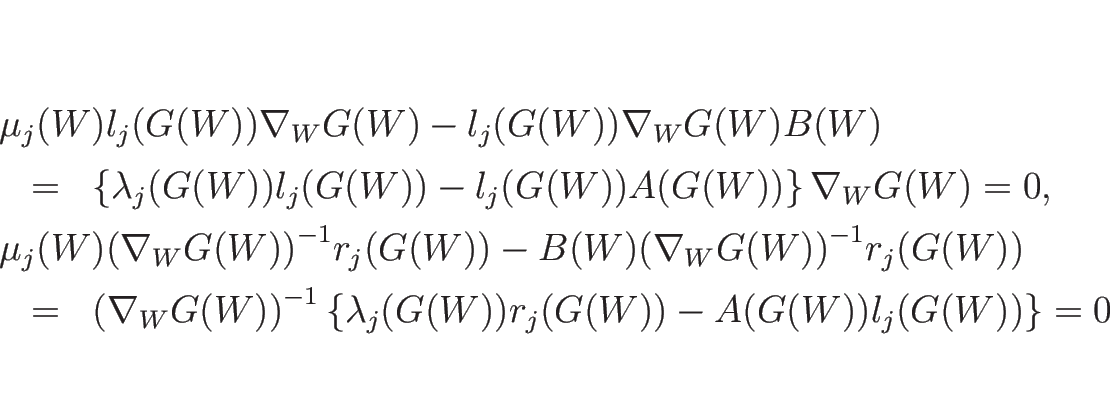
![]() を (3.3) の
を (3.3) の
![]() -リーマン不変量とし、
-リーマン不変量とし、![]() とすると、
とすると、
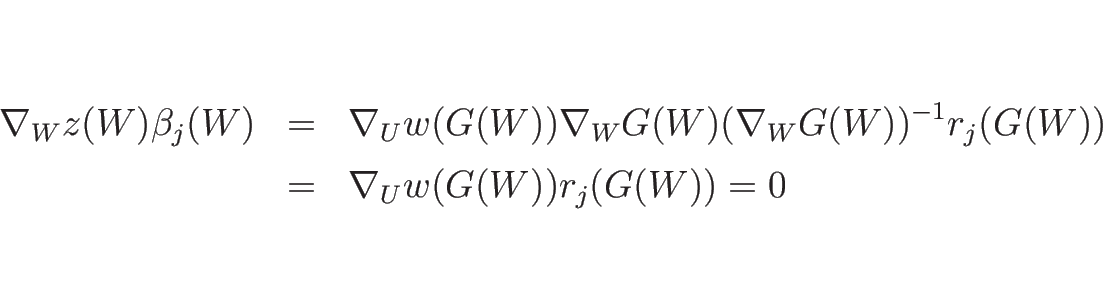
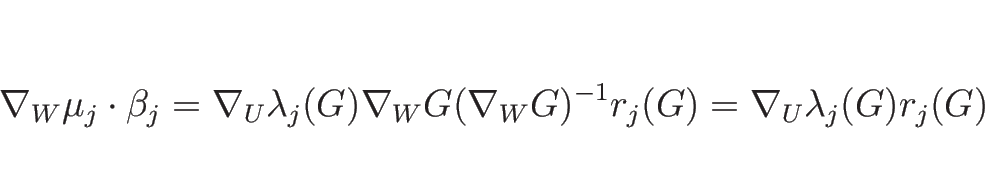
![]() の式に直して考えてもよい
ので、それで考える。
(3.12) の第 1 式、第 2 式より、
の式に直して考えてもよい
ので、それで考える。
(3.12) の第 1 式、第 2 式より、
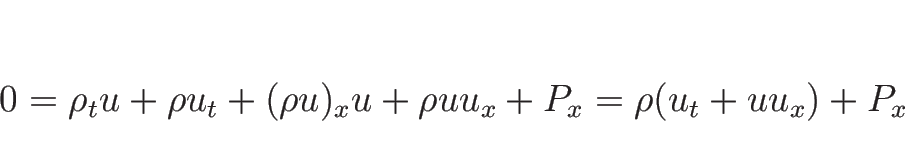
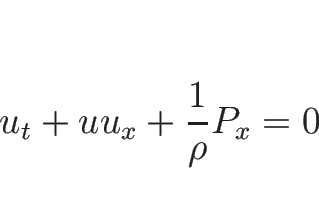
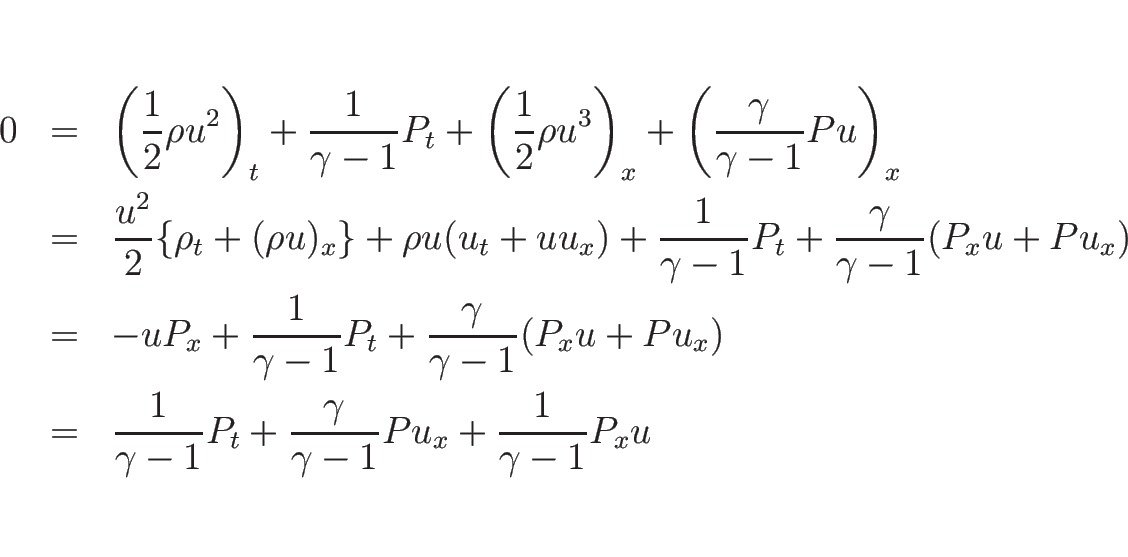
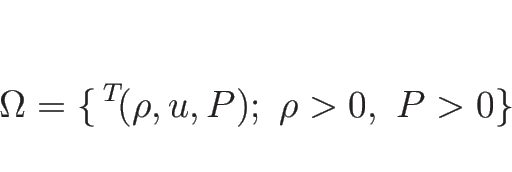
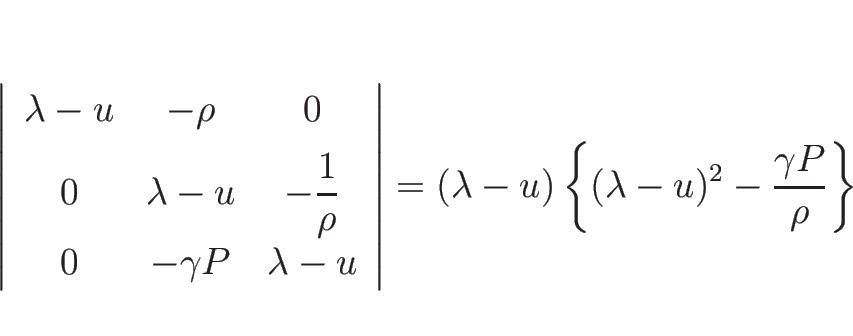
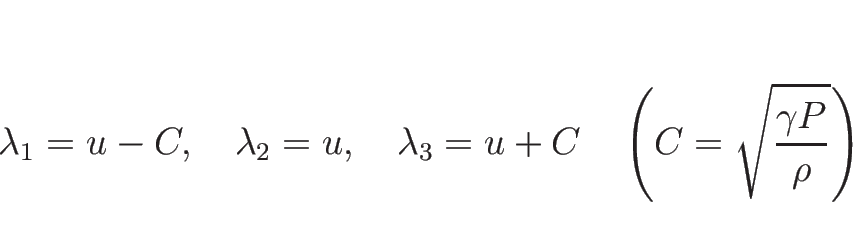
![\begin{displaymath}
r_1=\left[\begin{array}{c}-\rho\\ C\\ -\gamma P\end{array}\r...
..._3=\left[\begin{array}{c}\rho\\ C\\ \gamma P\end{array}\right]
\end{displaymath}](img344.png)
![]() ,
, ![]() なので、
なので、
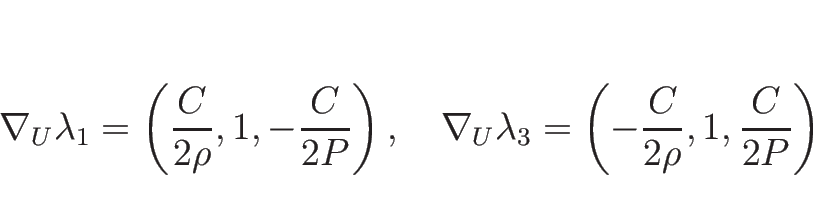
![]() より
より
![]() であるので、2-特性方向は線形退化となる。
よって、2-特性方向には膨張波解は存在しない。
であるので、2-特性方向は線形退化となる。
よって、2-特性方向には膨張波解は存在しない。
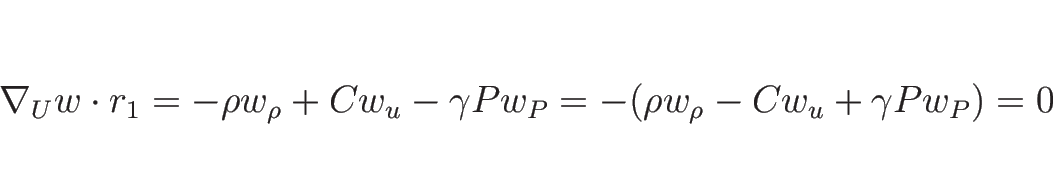
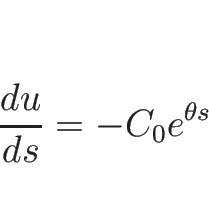
![]() となるものだから、
(3.17) で
となるものだから、
(3.17) で ![]() を消去すると、
を消去すると、
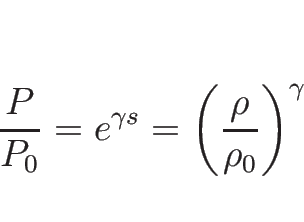
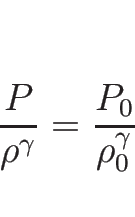
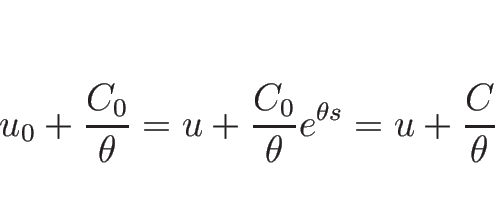
![\begin{displaymath}
\nabla_U w\cdot r_1 = \left[\begin{array}{c}1\\ 0\\ 0\end{array}\right]r_1=1
\end{displaymath}](img366.png)
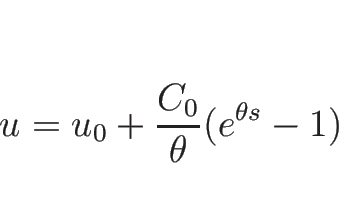
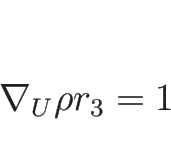
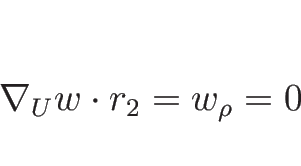
![]() は、
は、
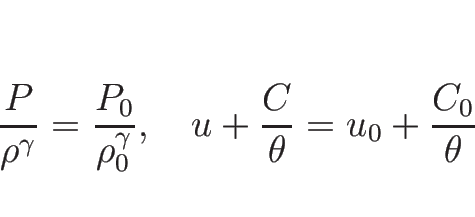
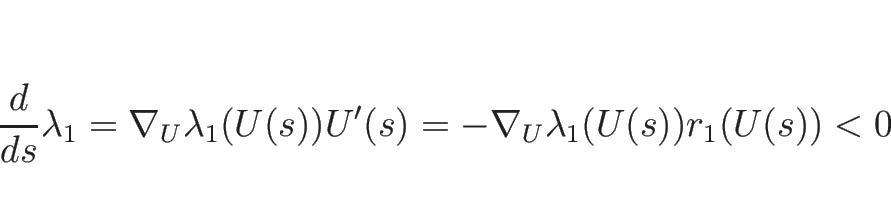
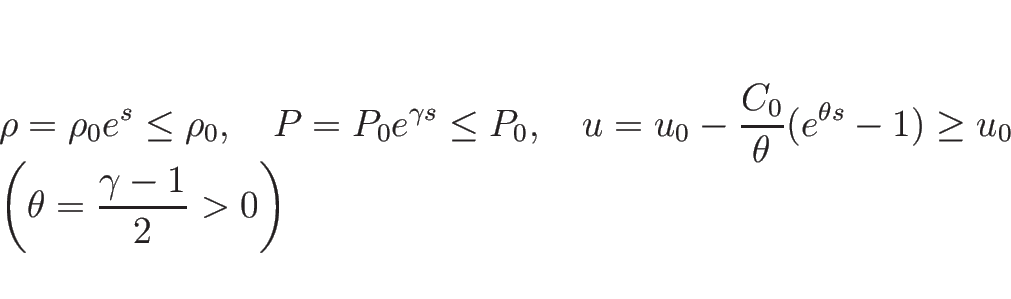
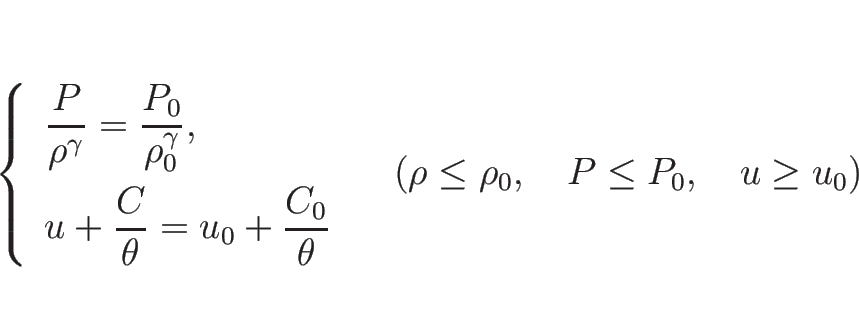
![]() とすれば
とすれば ![]() で、丁度
で、丁度
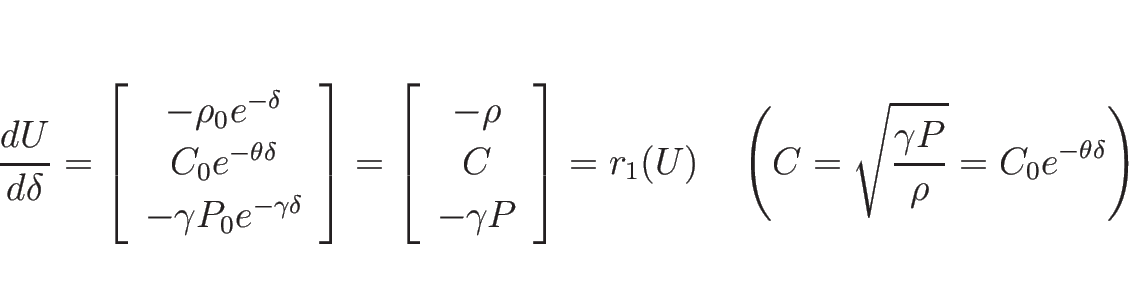
![]() は、(3.8) より
は、(3.8) より
![]() を満たす必要があるので、
を満たす必要があるので、
![]() によるパラメータ表示の式を代入すれば、
によるパラメータ表示の式を代入すれば、
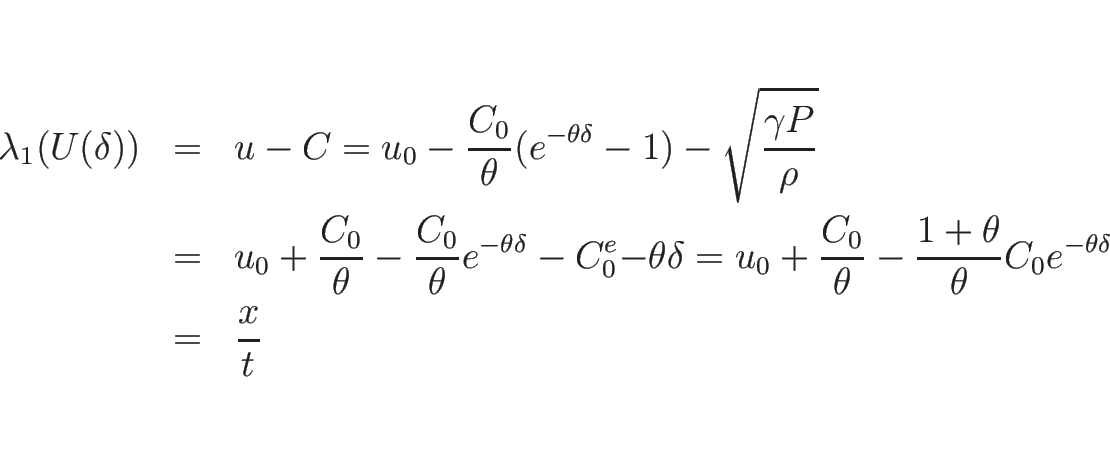
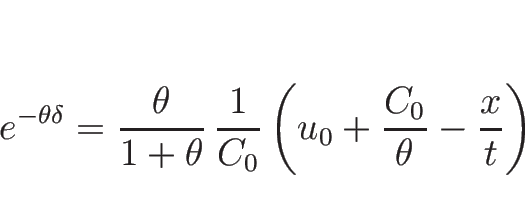
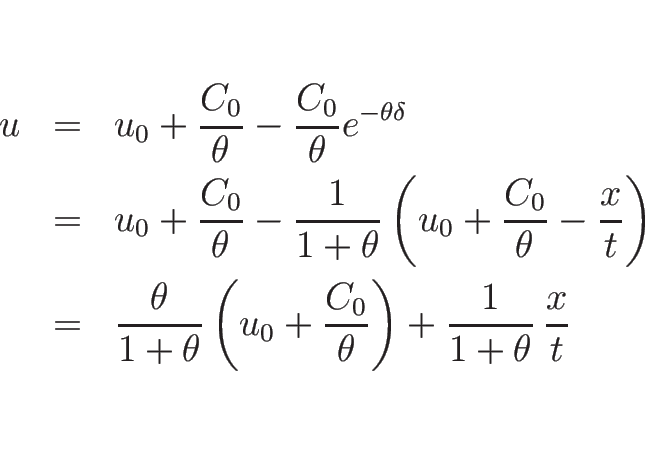
![]() は、
は、