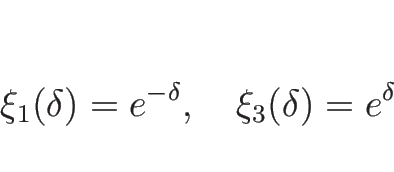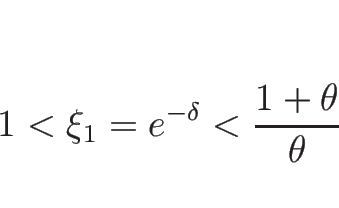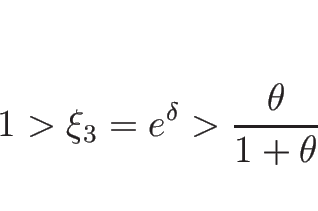4.8 オイラー座標系の理想気体の場合
ここでは、オイラー座標系での理想気体の保存則方程式系
(3.12) の不連続解である 1-衝撃波、3-衝撃波、
2-接触不連続を求めてみる。
ランキン-ユゴニオ条件はこの場合、
![\begin{displaymath}
\begin{array}{l}
s[\rho]=[\rho u],\\
s[\rho u]=[\rho u^2...
...ht]
= \left[\frac{1}{2}\rho u^3+\rho eu+Pu\right]
\end{array}\end{displaymath}](img773.png) |
(4.91) |
となる。ここで、![$[U]=U-U_0$](img774.png) とする (
とする (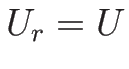 ,
, 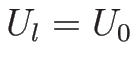 )。
)。
まずは 2-接触不連続を求める。
この場合、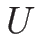 は
は
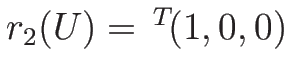 の積分曲線であるから、
の積分曲線であるから、
すなわち 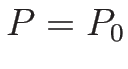 ,
, 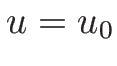 がその曲線となる。
がその曲線となる。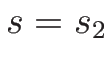 は
は
となる。この ![$[u]=[P]=0$](img783.png) ,
, 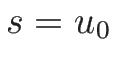 が
(4.42) を満たすことは、
が
(4.42) を満たすことは、
等より容易に検証できる。
この接触不連続は、固有ベクトルの積分曲線上を動くから、
2-リーマン不変量 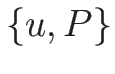 を定数にするもの、
と考えることもできる。
よって、2-接触不連続曲線
を定数にするもの、
と考えることもできる。
よって、2-接触不連続曲線 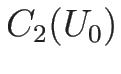 は
は
となる。
次は衝撃波を求める。
(4.42) の 1 本目と 2 本目の式から
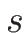 を消去すると
を消去すると
となる。ここで、(4.20) より、一般に
が成り立つので、
となり、よって
![\begin{displaymath}
\rho_0\rho[u]^2=[\rho][P]\end{displaymath}](img794.png) |
(4.93) |
が得られる。
また、(4.42) の 1 本目と 3 本目の式から
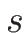 を消去すると
を消去すると
となるので、同様に (4.43) を使えば
![\begin{displaymath}
\rho_0\rho[u][B]=[\rho][Pu]\end{displaymath}](img796.png) |
(4.94) |
が得られるが、
なので、(4.45) は
と変形でき、これに (4.44) を代入すると、
となる。ここで (4.20) より、
であるから足して 2 で割れば
となるので、結局
が残ることになる。今 ![$[u]\neq 0$](img803.png) であることを示そう。
もし
であることを示そう。
もし ![$[u]=0$](img804.png) であると、(4.42) より
であると、(4.42) より
となり、衝撃波では
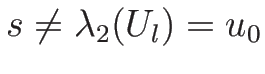 なので
なので ![$[\rho]=0$](img807.png) となり、
となり、
となるので ![$[U]=0$](img809.png) となってしまって不連続でなくなる。
よって
となってしまって不連続でなくなる。
よって ![$[u]\neq 0$](img803.png) でなければならない。
よって、
でなければならない。
よって、
となる。これを展開して 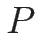 について解けば
について解けば
となるので、
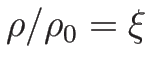 (
( ) と置くと、
) と置くと、
となる。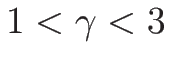 より
より  なので、
なので、
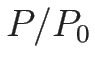 が正であるためには
が正であるためには
である必要がある。
そして、(4.44) より、
よって、
となる。以上により、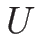 は
は 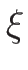 によって
によって
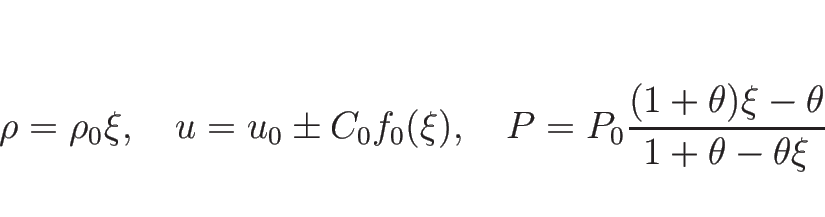 |
(4.95) |
のように表されることになる。
なお、これは  での表現であり、
厳密には
での表現であり、
厳密には 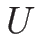 ではなく、命題 3.2 の
ではなく、命題 3.2 の 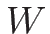 に
相当する。
この場合、命題 3.2 より、例えば接触不連続の条件
(4.39) は、
に
相当する。
この場合、命題 3.2 より、例えば接触不連続の条件
(4.39) は、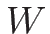 で言えば
で言えば
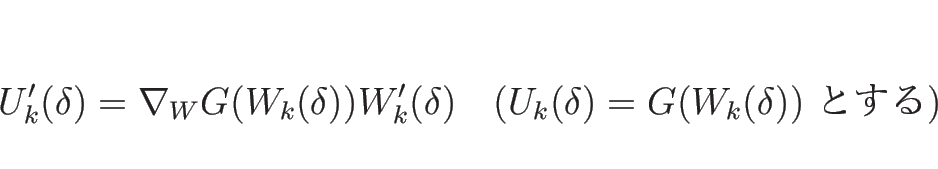 |
(4.96) |
より
となるので、 の固有値、固有ベクトルで考えればよいことがわかる。
衝撃波については、(4.34), (4.35) は次のようになる。
の固有値、固有ベクトルで考えればよいことがわかる。
衝撃波については、(4.34), (4.35) は次のようになる。
命題 4.4
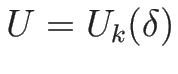 ,
, 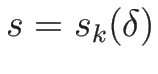 が
(4.34), (4.35) を
満たすとき、
が
(4.34), (4.35) を
満たすとき、
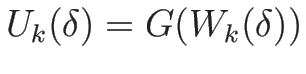 とするとき、
とするとき、
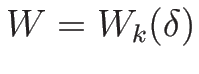 に対して次が成り立つ:
に対して次が成り立つ:
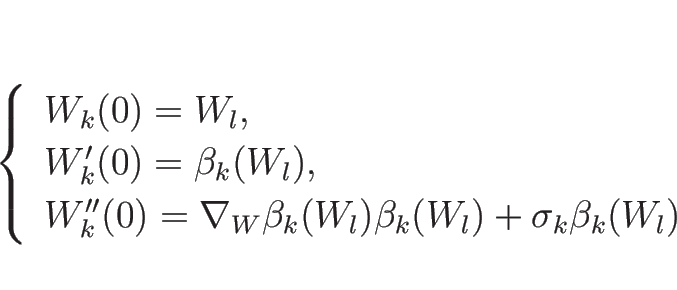 |
(4.97) |
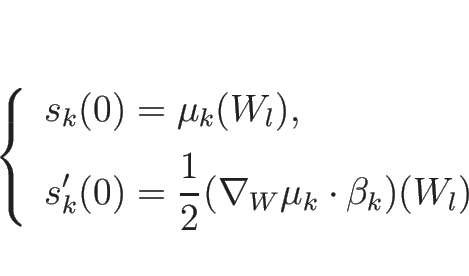 |
(4.98) |
(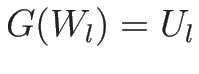 )
)
証明
命題 3.2 より
(4.49) の方は明らかに成り立つ。
また、(4.48) の最初の 2 本も
命題 3.2 と
式 (4.47) より明らか。
よって、(4.48) の最後の式のみを示す。
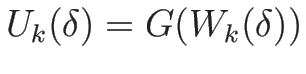 を
を 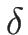 で 2 階微分すると
で 2 階微分すると
となるので  を代入すると
を代入すると
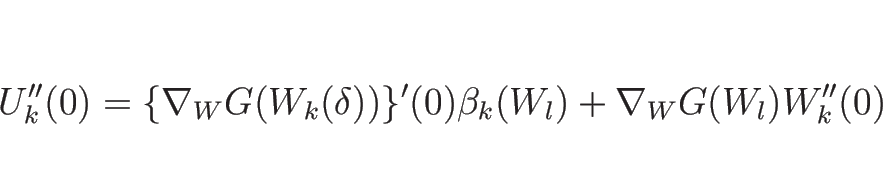 |
(4.99) |
となる。
一方、命題 3.2 より
であるので、この式を 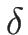 で微分すると
で微分すると
となり、 とすれば
とすれば
となるので、(4.50) と
(4.51) の両辺を引き算すると、
となる。(4.34) より、この左辺は
となるので、これで (4.48) の最後の式が得られる。
よって、(4.34), (4.35) を
考えるときは 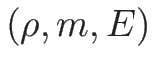 で考えても
で考えても 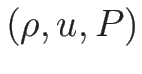 で考えても、
同じ形で書けることになる。
で考えても、
同じ形で書けることになる。
式 (4.46) に戻る。
今、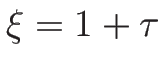 として
として 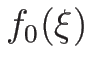 を
を 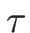 に関して
マクローリン展開すると
に関して
マクローリン展開すると
となるので、
であることがわかる。同様に、
なので、
となる。よって、(4.46) の 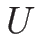 を
を
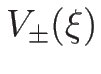 と書くことにすると、
と書くことにすると、
となるので、
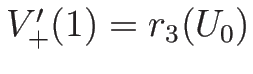 ,
,
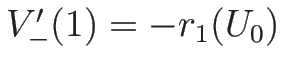 となる。
となる。
これを 4.7 節の 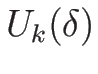 と比較すると、
と比較すると、
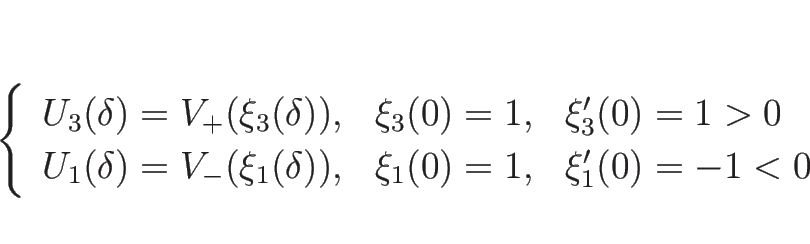 |
(4.101) |
のように書けることがわかり、よって、
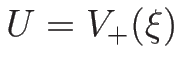 (
(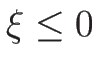 ) が 3-衝撃波曲線、
) が 3-衝撃波曲線、
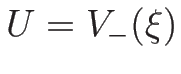 (
(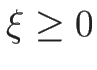 ) が 1-衝撃波曲線を与える。
) が 1-衝撃波曲線を与える。
衝撃波速度 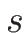 は、
は、
によって与えられる (複号は 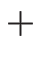 が
が 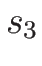 ,
,  が
が 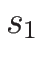 )。
)。
なので、(3.15) より
となるので、確かに
となる。
また、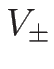 の 2 階微分の
の 2 階微分の 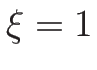 での値も、
での値も、
と求められる。
補題 4.2 に従って、
この 2 階微分の値と
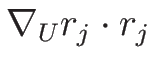 の値を比較してみる。
の値を比較してみる。
であるから、
となる。
よって、(4.52) にさらに
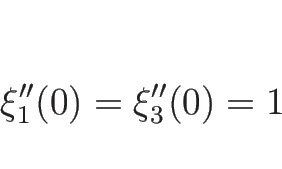 |
(4.103) |
であれば、
となるので、この 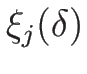 によって
補題 4.2 を満たす
によって
補題 4.2 を満たす 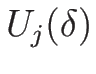 が
作れることになる。
が
作れることになる。
(4.52), (4.54) を満たす
満たす 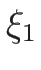 ,
, 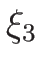 は、例えば
は、例えば
と取ればよいから、(4.46) の
 の方 (
の方 (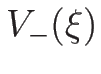 ) に
) に
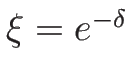 (
(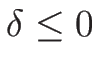 ) を
代入したのが 1-衝撃波曲線、
) を
代入したのが 1-衝撃波曲線、
 の方(
の方(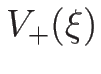 ) に
) に
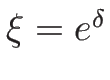 (
(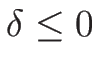 ) を
代入したのが 3-衝撃波曲線となる
(
) を
代入したのが 3-衝撃波曲線となる
(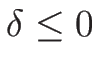 は補題 4.3 より)。
ただし、
は補題 4.3 より)。
ただし、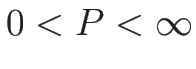 である必要があるので、1-衝撃波では
である必要があるので、1-衝撃波では
3-衝撃波では
の範囲である必要がある。
竹野茂治@新潟工科大学
2018-08-01
![\begin{displaymath}
\begin{array}{l}
s[\rho]=[\rho u],\\
s[\rho u]=[\rho u^2...
...ht]
= \left[\frac{1}{2}\rho u^3+\rho eu+Pu\right]
\end{array}\end{displaymath}](img773.png)
![]() は
は
![]() の積分曲線であるから、
の積分曲線であるから、
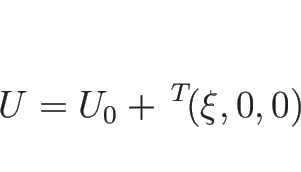
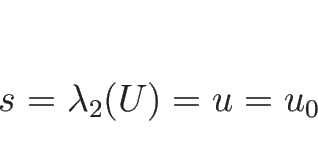
![\begin{displaymath}[\rho u]=u_0[\rho]=s[\rho],
\hspace{1zw}\rho e=\frac{1}{\gamma-1}P,
\hspace{1zw}\rho eu+Pu=\frac{\gamma}{\gamma-1}Pu
\end{displaymath}](img785.png)
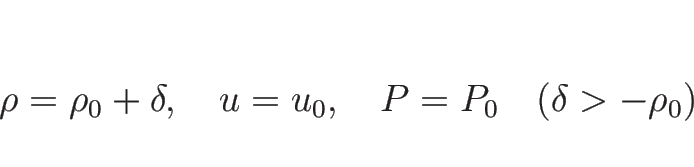
![]() を消去すると
を消去すると
![\begin{displaymath}[\rho][\rho u^2+P]=[\rho u]^2
\end{displaymath}](img789.png)
![\begin{displaymath}[\rho u]^2-[\rho][\rho u^2]=\rho_0\rho[u]^2
\end{displaymath}](img793.png)
![]() を消去すると
を消去すると
![\begin{displaymath}[\rho][\rho Bu+Pu]=[\rho u][\rho B]
\hspace{1zw}\left(B=\frac{u^2}{2}+e=\frac{u^2}{2}+\frac{P}{(\gamma-1)\rho}\right)
\end{displaymath}](img795.png)
![\begin{displaymath}[u][B]
=\frac{1}{2}[u][u^2]+\frac{1}{\gamma-1}[u]\left[\frac{...
...+u_0}{2}[u]^2+\frac{1}{\gamma-1}[u]\left[\frac{P}{\rho}\right]
\end{displaymath}](img797.png)
![\begin{displaymath}
\rho_0\rho\frac{u+u_0}{2}[u]^2
+\frac{\rho_0\rho}{\gamma-1}[u]\left[\frac{P}{\rho}\right]
=[\rho][Pu]
\end{displaymath}](img798.png)
![\begin{displaymath}
\frac{u+u_0}{2}[\rho][P]
+\frac{\rho_0\rho}{\gamma-1}[u]\left[\frac{P}{\rho}\right]
=[\rho][Pu]
\end{displaymath}](img799.png)
![\begin{displaymath}[Pu]=P[u]+u_0[P]=P_0[u]+u[P]
\end{displaymath}](img800.png)
![\begin{displaymath}[Pu]=\frac{P+P_0}{2}[u]+\frac{u+u_0}{2}[P]
\end{displaymath}](img801.png)
![\begin{displaymath}
\frac{\rho_0\rho}{\gamma-1}[u]\left[\frac{P}{\rho}\right]
=\frac{P+P_0}{2}[\rho][u]
\end{displaymath}](img802.png)
![\begin{displaymath}
(s-u_0)[\rho]=0
\end{displaymath}](img805.png)
![\begin{displaymath}[\rho u^2+P]-s[\rho u]
=u_0^2[\rho]+[P]-s u_0[\rho]
=[P]
=0
\end{displaymath}](img808.png)
![\begin{displaymath}
\rho_0\rho\left[\frac{P}{\rho}\right]
=\theta(P+P_0)[\rho]
\hspace{1zw}\left(\theta=\frac{\gamma-1}{2}\right)
\end{displaymath}](img810.png)
![\begin{displaymath}
P=P_0\frac{\rho+\theta[\rho]}{\rho_0-\theta[\rho]}
=P_0\frac{(1+\theta)\rho-\theta\rho_0}{(1+\theta)\rho_0-\theta\rho}
\end{displaymath}](img811.png)
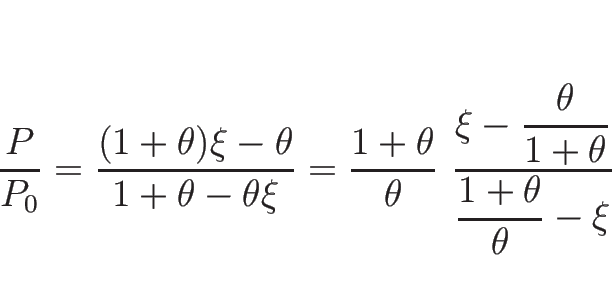
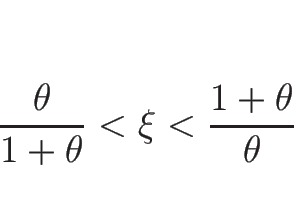
![\begin{eqnarray*}[u]^2
&=&
\frac{[\rho]}{\rho_0\rho}[P]
=
\frac{\xi-1}{\rho_...
...a\xi)}\,\frac{\gamma P_0}{\rho_0}
\hspace{1zw}(\gamma=2\theta+1)\end{eqnarray*}](img818.png)
![\begin{displaymath}[u]=\pm C_0f_0(\xi)
\hspace{1zw}\left(C_0=\sqrt{\frac{\gamma ...
...}f_0(\xi)=\frac{\xi-1}{\sqrt{\xi(1+\theta-\theta\xi)}}
\right)
\end{displaymath}](img819.png)
![]() での表現であり、
厳密には
での表現であり、
厳密には ![]() ではなく、命題 3.2 の
ではなく、命題 3.2 の ![]() に
相当する。
この場合、命題 3.2 より、例えば接触不連続の条件
(4.39) は、
に
相当する。
この場合、命題 3.2 より、例えば接触不連続の条件
(4.39) は、![]() で言えば
で言えば
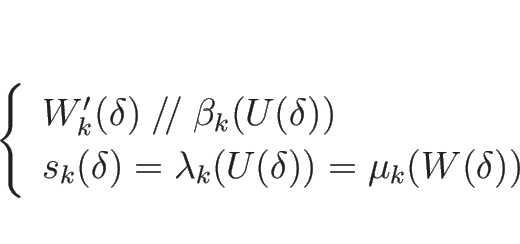
![]() ,
, ![]() が
(4.34), (4.35) を
満たすとき、
が
(4.34), (4.35) を
満たすとき、
![]() とするとき、
とするとき、
![]() に対して次が成り立つ:
に対して次が成り立つ:
![]() を
を ![]() で 2 階微分すると
で 2 階微分すると
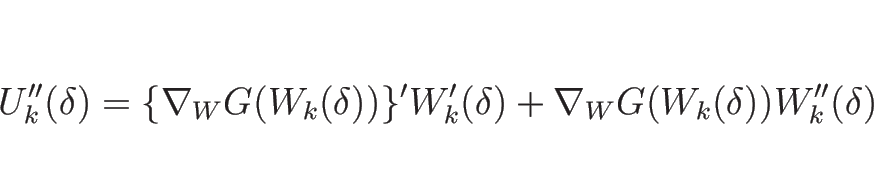
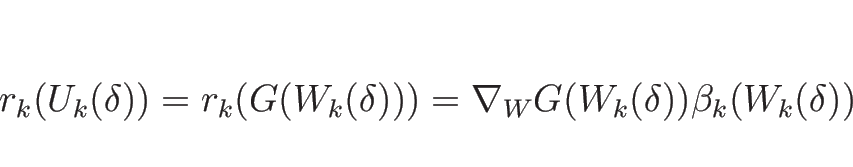
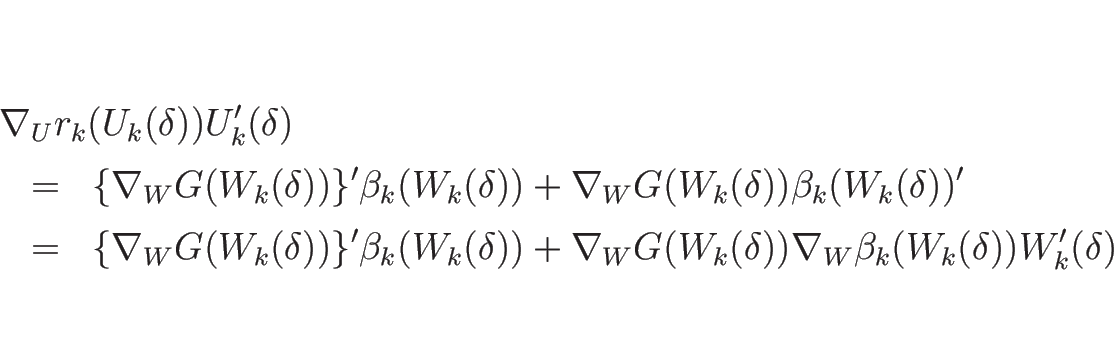
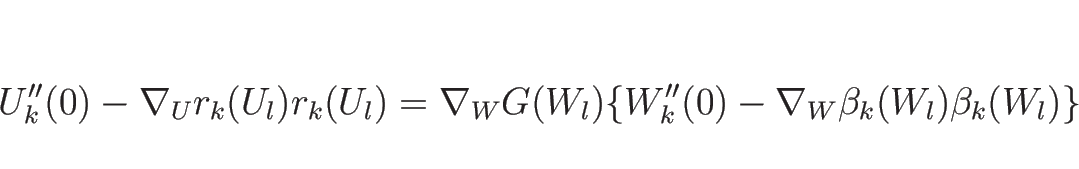
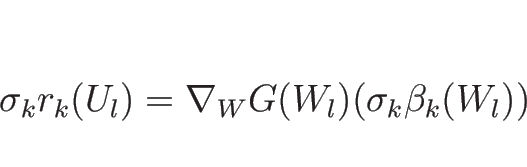
![]() で考えても
で考えても ![]() で考えても、
同じ形で書けることになる。
で考えても、
同じ形で書けることになる。
![]() として
として ![]() を
を ![]() に関して
マクローリン展開すると
に関して
マクローリン展開すると
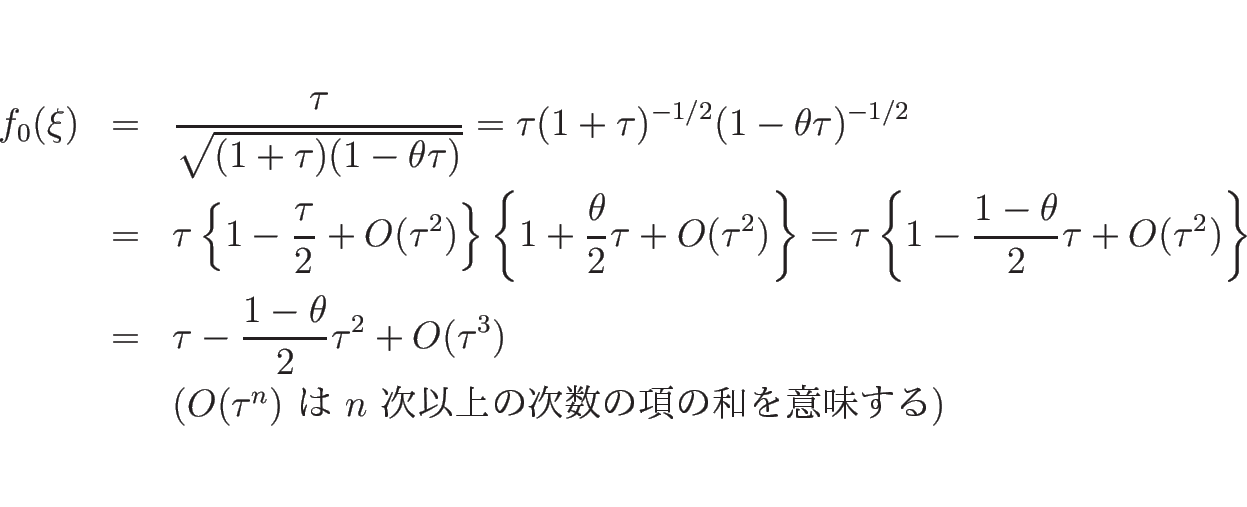
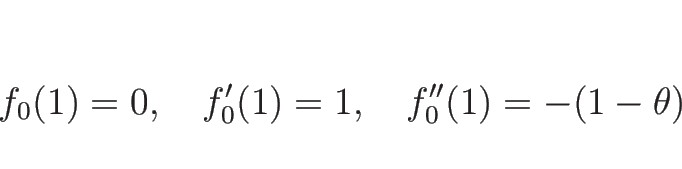
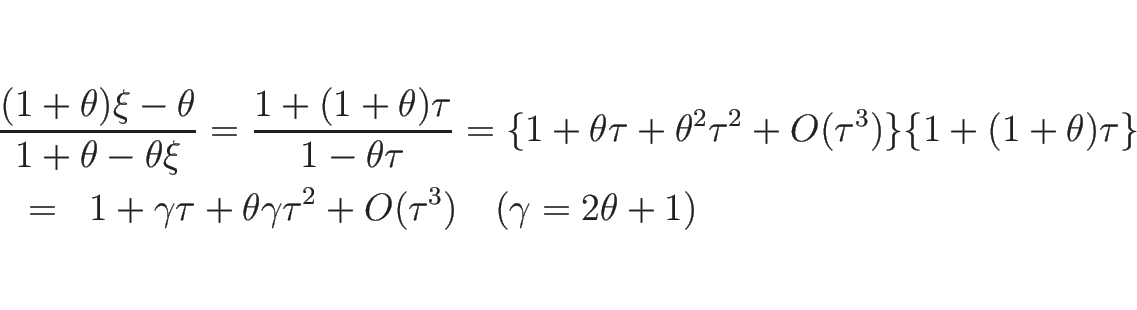
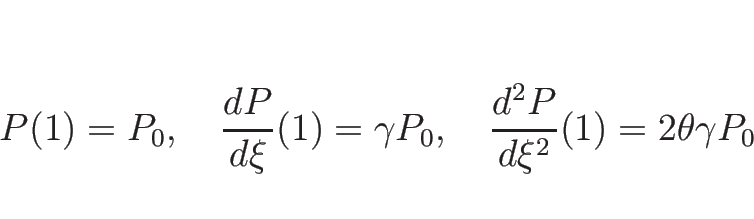
![\begin{displaymath}
V_{\pm}'(1)=\left[\begin{array}{c}\rho_0\\ \pm C_0\\ \gamma P_0\end{array}\right]
\end{displaymath}](img844.png)
![]() と比較すると、
と比較すると、
![]() は、
は、
![\begin{eqnarray*}s
&=&
\frac{[\rho u]}{[\rho]}
=
\frac{[\rho]u_0+\rho[u]}{[\...
..._0(\xi))
\\ &=&
u_0\pm C_0\sqrt{\frac{\xi}{1+\theta-\theta\xi}}\end{eqnarray*}](img853.png)
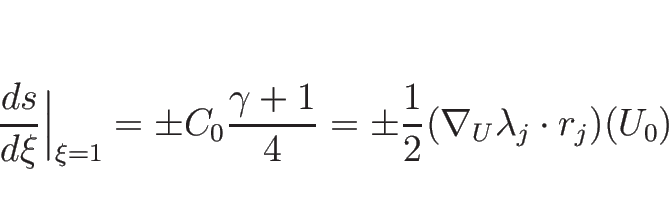
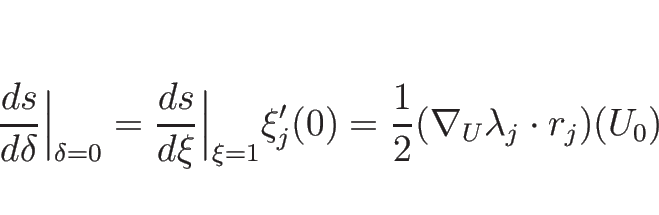
![]() の 2 階微分の
の 2 階微分の ![]() での値も、
での値も、
![\begin{displaymath}
V_{\pm}''(1)=\left[\begin{array}{c}0\\ \mp(1-\theta)C_0\\ 2\theta\gamma P_0\end{array}\right]
\end{displaymath}](img865.png)
![\begin{eqnarray*}\lefteqn{\nabla_Ur_1\cdot r_1}
\\ &=&
\nabla_U\left[\begin{ar...
...ft[\begin{array}{c}\rho\\ \theta C\\ \gamma^2 P\end{array}\right]\end{eqnarray*}](img867.png)
![\begin{eqnarray*}(\nabla_Ur_1\cdot r_1)(U_0)+r_1(U_0)
&=&
\left[\begin{array}{...
... P_0\end{array}\right]
=V_{+}''(1)\hspace{1zw}(\gamma-1=2\theta)\end{eqnarray*}](img868.png)
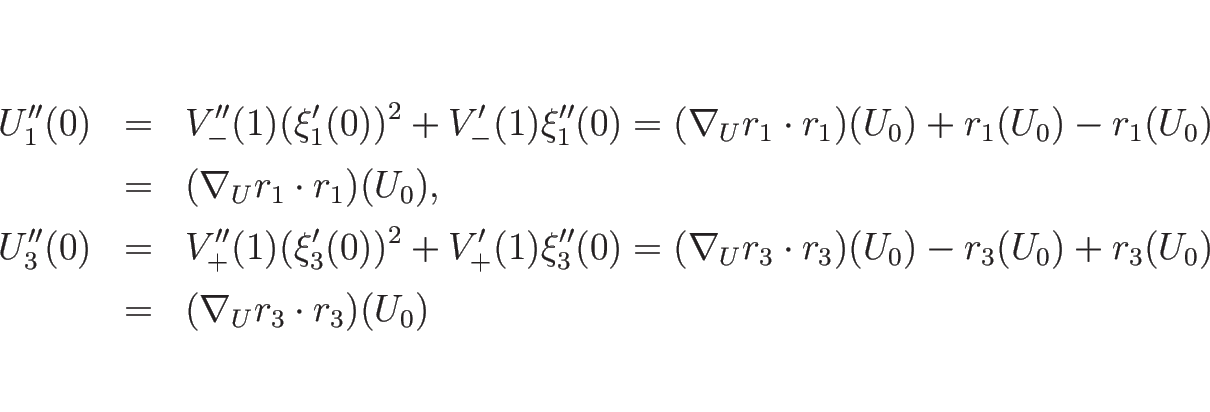
![]() ,
, ![]() は、例えば
は、例えば