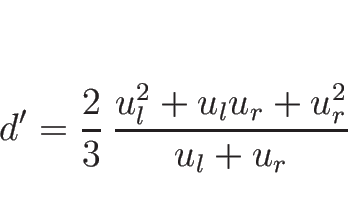4.4 ラグランジュ座標系での不連続性
ここまでの、4.2, 4.3 節での考察は オイラー座標系での話であったので、
ラグランジュ座標系 (質量座標系) の方程式に
そのまま同じような形で成り立つかどうかは定かではない。
しかも、2.6 節での ラグランジュ座標系の方程式の導出は、解がなめらかであるとして
式変形を行っているので、不連続な解に対してはそこでの計算は意味を持たず、
不連続な解に関する両座標系での対応は不明である。
よって、ここでは 4.2 節で得られた
ランキン-ユゴニオ条件が、ラグランジュ座標系ではどのようになるのかを
考えてみることにする。
まず、ここでは簡単のため
のように書くこととし、オイラー座標系での方程式を
![\begin{displaymath}
U_t+F(U)_x=0,
\hspace{1zw}U=\left[\begin{array}{c}\rho\\ \...
...gin{array}{c}\rho u\\ \rho u^2+P\\ \rho uB+Pu\end{array}\right]\end{displaymath}](img612.png) |
(4.64) |
ラグランジュ座標系での方程式を
![\begin{displaymath}
\tilde{V}_{\tau}+\tilde{G}(\tilde{V})_z=0,
\hspace{1zw}\ti...
...{array}{c}-\tilde{u}\\ \tilde{P}\\ \tilde{Pu}\end{array}\right]\end{displaymath}](img613.png) |
(4.65) |
のように書くこととする。
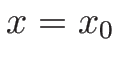 は、不連続線
は、不連続線 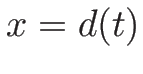 より左にあるとし、
より左にあるとし、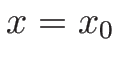 から右にみて
最初にあらわれる不連続線が
から右にみて
最初にあらわれる不連続線が 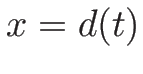 であるとする。
この
であるとする。
この 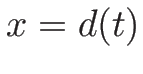 を質量座標で表した曲線を
を質量座標で表した曲線を
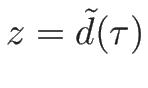 とすると、
とすると、
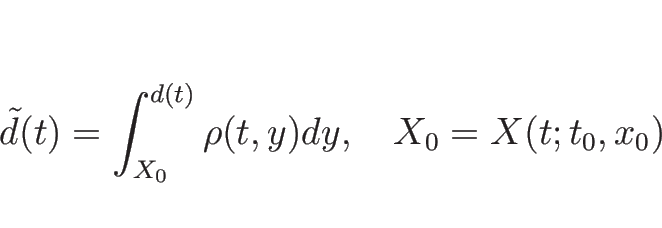 |
(4.66) |
が 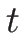 に対して成り立つことになる。
この積分の中に現れる
に対して成り立つことになる。
この積分の中に現れる 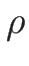 は、
は、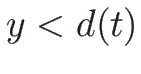 なのでなめらかな関数であり、
方程式 (4.15) を満たすことに注意する。
この式 (4.17) を
なのでなめらかな関数であり、
方程式 (4.15) を満たすことに注意する。
この式 (4.17) を 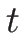 で微分すると、
(2.5) より、
で微分すると、
(2.5) より、
となるので、
よって、
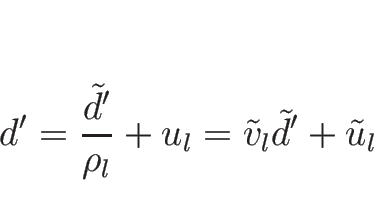 |
(4.67) |
となることがわかる。なお、ここでは簡単のため、
のように書くことにする。
この関係式 (4.18) を用いて、
オイラー座標系に対するランキン-ユゴニオ条件
![\begin{displaymath}
\left\{\begin{array}{l}
d'[\rho]=[\rho u]\\
d'[\rho u]=[\rho u^2+P]\\
d'[\rho B]=[\rho uB+Pu]
\end{array}\right.\end{displaymath}](img621.png) |
(4.68) |
からラグランジュ座標系の関係式を導くことにする。
まず、
より、
![\begin{displaymath}[fg]=[f]g_r+f_l[g]=[f]g_l+f_r[g]\end{displaymath}](img623.png) |
(4.69) |
であることに注意する。
まず、(4.19) の第 1 式に (4.18) を代入すると、
となる。ここで、
より、
となる。よって結局
![\begin{displaymath}[\tilde{u}]=-\tilde{d}'[\tilde{v}]\end{displaymath}](img627.png) |
(4.70) |
が得られることになる。
次に、(4.19) の第 2 式に (4.18) を代入すると、
となるが、(4.21) を代入すると
となるので、結局
![\begin{displaymath}[\tilde{P}]=\tilde{d}'[\tilde{u}]\end{displaymath}](img630.png) |
(4.71) |
が得られる。
同様に、(4.19) の第 3 式は、
(4.21) を用いれば、
より、
![\begin{displaymath}[\tilde{P}\tilde{u}]=\tilde{d}'[\tilde{B}]\end{displaymath}](img632.png) |
(4.72) |
が得られる。
結局、(4.21), (4.22), (4.23) により、
ラグランジュ座標系でもオイラー座標系の場合と同形のランキン-ユゴニオ条件
が成り立つことになる。
一般に、保存則方程式 (4.1) が
別の形の発散形
に書き直すことができるとき、それで不連続線に関する条件を
としていいかというとそうではない。例えば、単独保存則
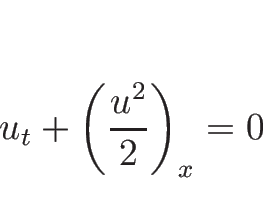 |
(4.73) |
に対するランキン-ユゴニオ条件は、
すなわち、
となるが、この (4.24) は、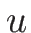 がなめらかならば、
がなめらかならば、
と書くこともでき、これに対するランキン-ユゴニオ条件を考えると
すなわち、
となり、ランキン-ユゴニオ条件の意味するものが変わってしまう。
つまり、保存則方程式のランキン-ユゴニオ条件を考える場合は、
解がなめらかであると見て方程式を変形して、
別の保存系に書き直してはいけない、ということになる。
その意味では、2.6 節の
ラグランジュ座標系の方程式の導出では、解がなめらかであるとして
無理矢理保存系の形に書き直したようにも見えるが実はそうではなく、
この節の結果により、その形 (4.16) が
オイラー座標系の保存則方程式 (4.15) に
ちゃんと対応した形のものであることを意味している。
竹野茂治@新潟工科大学
2018-08-01
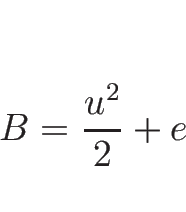
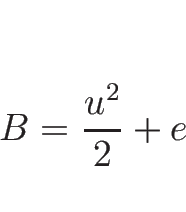
![]() は、不連続線
は、不連続線 ![]() より左にあるとし、
より左にあるとし、![]() から右にみて
最初にあらわれる不連続線が
から右にみて
最初にあらわれる不連続線が ![]() であるとする。
この
であるとする。
この ![]() を質量座標で表した曲線を
を質量座標で表した曲線を
![]() とすると、
とすると、
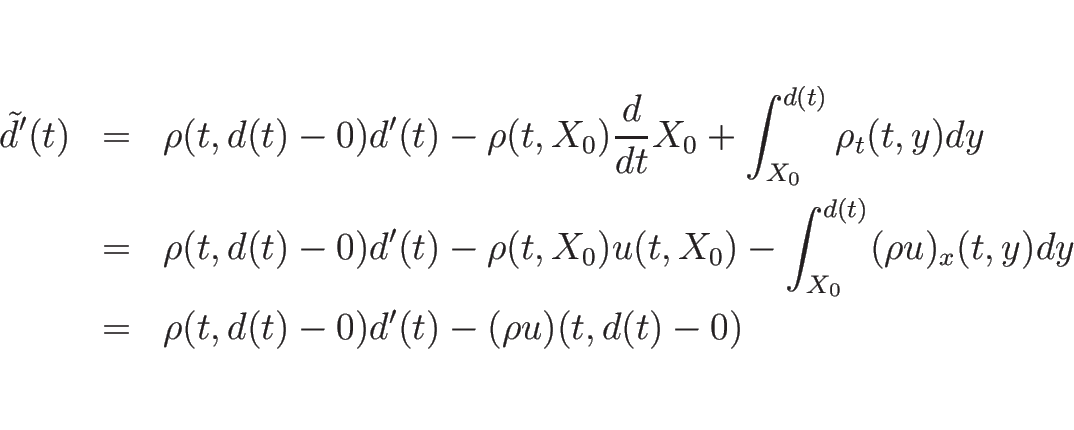
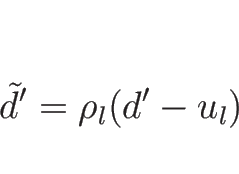
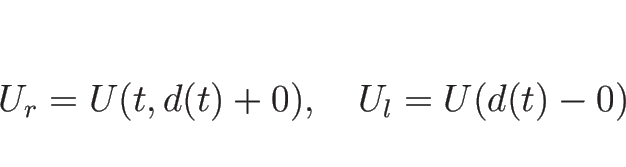
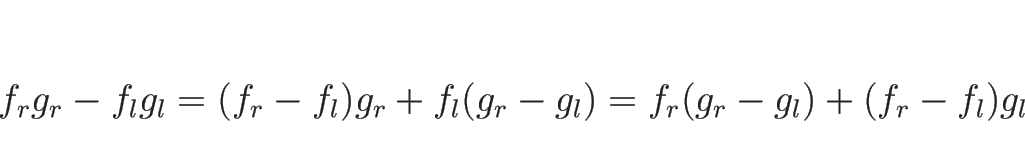
![\begin{eqnarray*}0
&=&
[\rho u]-d'[\rho]
=
[\tilde{\rho}\tilde{u}]-(\tilde...
...\tilde{d}'\frac{\tilde{v}_l}{\tilde{\rho}_r}[\tilde{\rho}]\right)\end{eqnarray*}](img624.png)
![\begin{displaymath}
\frac{\tilde{v}_l}{\tilde{\rho}_r}[\tilde{\rho}]
=\frac{\til...
...e{v}_r
=-[\tilde{v}]
\hspace{1zw}\left(v=\frac{1}{\rho}\right)
\end{displaymath}](img625.png)
![\begin{displaymath}
0=\tilde{\rho}_r([\tilde{u}]+\tilde{d}'[\tilde{v}])
\end{displaymath}](img626.png)
![\begin{eqnarray*}0
&=&
[\rho u^2+P]-d'[\rho u]
=
[\tilde{\rho}\tilde{u}^2]+[...
...de{u}_r[\tilde{u}]
-\tilde{d}'\tilde{v}_l[\tilde{\rho}\tilde{u}]\end{eqnarray*}](img628.png)
![\begin{displaymath}
\tilde{\rho}_r\tilde{u}_r[\tilde{u}]
-\tilde{d}'\tilde{v}_l[...
...de{d}'[\tilde{\rho}\tilde{u}\tilde{v}]
=
-\tilde{d}[\tilde{u}]
\end{displaymath}](img629.png)
![\begin{eqnarray*}0
&=&
[\rho uB+Pu]-d'[\rho B]
=
[\tilde{\rho}\tilde{u}\tild...
...tilde{B}]
%\\ &=&
=
[\tilde{P}\tilde{u}]-\tilde{d}'[\tilde{B}]\end{eqnarray*}](img631.png)
![\begin{displaymath}[\tilde{G}(\tilde{V})]=\tilde{d}'[\tilde{V}]\end{displaymath}](img633.png)
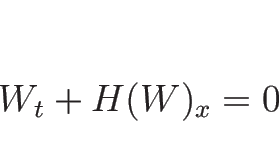
![\begin{displaymath}
d'[W]=[H(W)]
\end{displaymath}](img635.png)
![\begin{displaymath}
d'[u]=\left[\frac{u^2}{2}\right]=\frac{u_r^2-u_l^2}{2}
=\frac{u_l+u_r}{2}[u]
\end{displaymath}](img637.png)
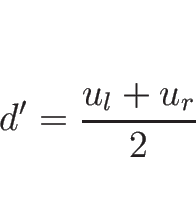
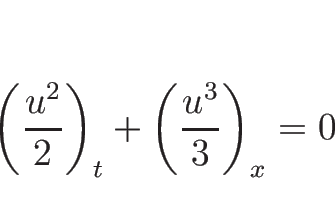
![\begin{displaymath}
d'\left[\frac{u^2}{2}\right]=\left[\frac{u^3}{3}\right]
=\frac{1}{3}[u](u_l^2+u_l u_r+u_r^2)
\end{displaymath}](img640.png)