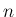
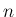 が偶数で、
が偶数で、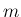 が奇数の場合を考える。
が奇数の場合を考える。
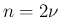 ,
, 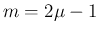 とすると、
とすると、
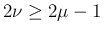 より
より 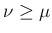 であり、
であり、
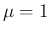 のときは (3) より無限大となるから、
ここでは
のときは (3) より無限大となるから、
ここでは
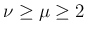 であるとする。
であるとする。
(5) より、
であり、補題 2, 3 より、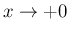 に対し、
に対し、
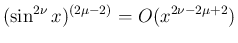
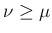 より (25) で
より (25) で 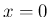 とすると、
となることがわかる。
すなわち、(25) の
とすると、
となることがわかる。
すなわち、(25) の 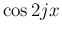 の係数の和が 0 と
なるので、補題 1 と (24),
(25) より
の係数の和が 0 と
なるので、補題 1 と (24),
(25) より
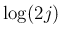 の部分は、
とすることもできる (
の部分は、
とすることもできる (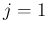 の項は
の項は 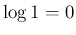 により消える)。
元の
により消える)。
元の 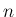 ,
, 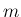 で表すと、
で表すと、
竹野茂治@新潟工科大学