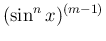
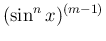 が
が
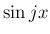 で表せる場合は、前節の
で表せる場合は、前節の 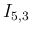 と同様に
ディリクレ積分に帰着して値が求まるが、
と同様に
ディリクレ積分に帰着して値が求まるが、
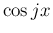 が現れる場合はそうはいかない。
が現れる場合はそうはいかない。
一般に 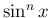 は、
は、
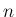 が奇数であれば
が奇数であれば 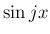 の線形結合で、
の線形結合で、
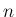 が偶数であれば
が偶数であれば 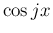 と 1 の線形結合で表わされる。
よって、
と 1 の線形結合で表わされる。
よって、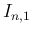 で
で 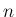 が奇数の場合は (9) により
ディリクレ積分に帰着し、よってそれが有限値となることがわかるし、
また、
が奇数の場合は (9) により
ディリクレ積分に帰着し、よってそれが有限値となることがわかるし、
また、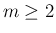 の場合
の場合
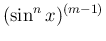 は、
は、
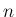 が奇数、
が奇数、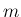 が奇数であれば
が奇数であれば 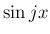 の線形結合
の線形結合
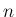 が奇数、
が奇数、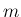 が偶数であれば
が偶数であれば 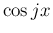 の線形結合
の線形結合
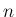 が偶数、
が偶数、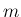 が奇数であれば
が奇数であれば 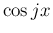 の線形結合
の線形結合
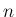 が偶数、
が偶数、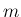 が偶数であれば
が偶数であれば 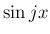 の線形結合
の線形結合
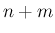 が偶数の場合は
ディリクレ積分に帰着し、
が偶数の場合は
ディリクレ積分に帰着し、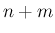 が奇数の場合は
が奇数の場合は 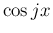 が
残ることになる。
が
残ることになる。
ここで、
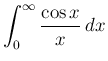
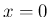 の近くで積分は収束せず、
また
の近くで積分は収束せず、
また
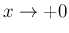 で有界となるように
で有界となるように
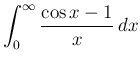
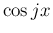 が残る場合の積分には注意が必要である。
が残る場合の積分には注意が必要である。
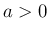 ,
, 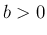 に対し、
に対し、
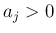 (
(
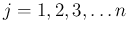 ),
),
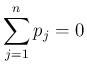 に対し、
に対し、
証明
1. 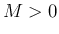 に対して
に対して
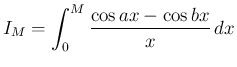
 で特異性を持たないように変形すると
で特異性を持たないように変形すると
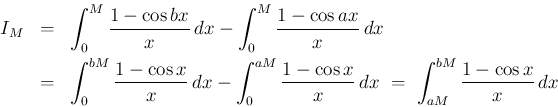
![\begin{eqnarray*}I_M
&=&
\int_{a}^{b}\frac{1-\cos Mx}{x}\, dx
\ =\
\int_{a}...
...{Mx}\right]_a^b
-\,\frac{1}{M}\int_a^b\frac{\sin Mx}{x^2}\, dx
\end{eqnarray*}](img74.png)
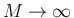 で
で 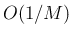 なので、
なので、
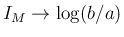 となる。
となる。
2.
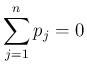 より
より
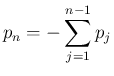 なので、
なので、
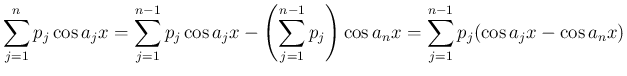
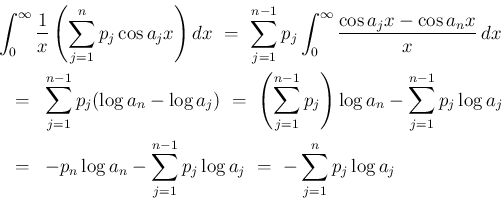
この補題により、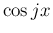 が残る場合は、
その係数の和が 0 であれば計算できることになる。
が残る場合は、
その係数の和が 0 であれば計算できることになる。
以上により、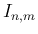 は、
は、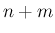 が偶数の場合は
が偶数の場合は 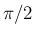 の有理数倍、
の有理数倍、
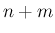 が奇数の場合は
が奇数の場合は 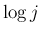 の有理数倍の和の形となることが
期待される。
の有理数倍の和の形となることが
期待される。
竹野茂治@新潟工科大学