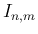
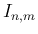 の計算の方針について考える。
の計算の方針について考える。
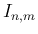 は部分積分により、
は部分積分により、
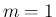 の場合に帰着する方向で計算することができる。
の場合に帰着する方向で計算することができる。
部分積分を繰り返すと一般に、
となるが、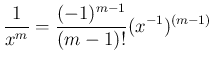
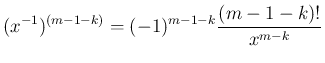
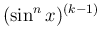 は
は
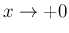 でのオーダーは
でのオーダーは
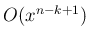 なので、
なので、
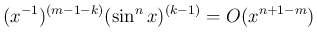
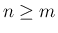 であれば、
(5) の和の部分は
であれば、
(5) の和の部分は
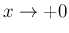 と
と
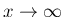 の両方で 0 になる。
よって、
の両方で 0 になる。
よって、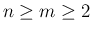 に対して
が成り立つことになる。
に対して
が成り立つことになる。
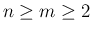 では
では 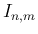 の収束性は保証されていたので、
その場合は (6) の右辺も収束することになる。
なお、(6) 自体は
の収束性は保証されていたので、
その場合は (6) の右辺も収束することになる。
なお、(6) 自体は 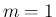 でも成立するが、
でも成立するが、
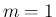 で
で 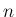 が奇数の場合の有限性はまだ保証はされない。
が奇数の場合の有限性はまだ保証はされない。
この (6) の右辺であるが、
被積分関数の分子は 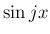 ,
, 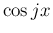 などで表すことができ、
それによってこの積分をディリクレ積分などに帰着させることができる。
おおまかにはこのような方針で
などで表すことができ、
それによってこの積分をディリクレ積分などに帰着させることができる。
おおまかにはこのような方針で 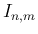 が計算できることになる。
が計算できることになる。
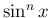 の導関数を
の導関数を 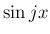 ,
, 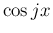 などに変形するのは、
微分を計算したあとで変形する方法と、
先に
などに変形するのは、
微分を計算したあとで変形する方法と、
先に 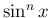 を変形してから微分する方法があるが、
もちろん後者の方が易しい。
例えば、
を変形してから微分する方法があるが、
もちろん後者の方が易しい。
例えば、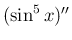 の場合、先に微分すると、
の場合、先に微分すると、
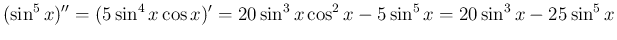
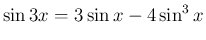 より、
より、
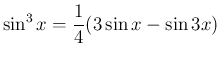
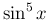 は、積・和の公式を用いれば、
は、積・和の公式を用いれば、
一方、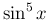 を先に (7) の形にしておけば、
を先に (7) の形にしておけば、
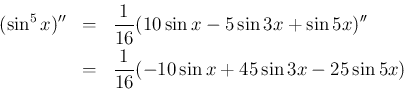
そして、 に対し、
に対し、
 は (6), (8), (9) より
は (6), (8), (9) より
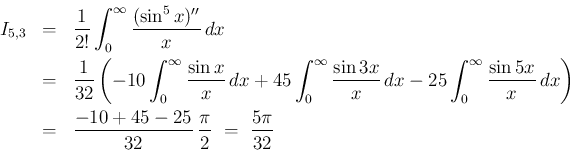
竹野茂治@新潟工科大学