6 y4 の場合
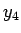 は、(6), (7) によって 1 から
は、(6), (7) によって 1 から 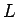 までの
整数が作られるので、この場合は、
までの
整数が作られるので、この場合は、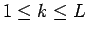 に対し、
に対し、
となる。ここで、
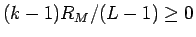 であるが、
であるが、
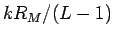 は、
は、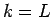 のとき、
のとき、
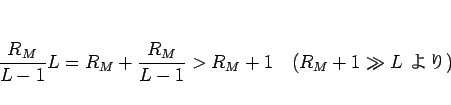
となってしまうので、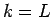 に対しては
補題 1 を適用できず、別に考える必要がある。
ただし、
に対しては
補題 1 を適用できず、別に考える必要がある。
ただし、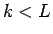 ならば、
ならば、
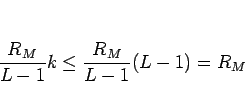
なので、補題 1 は適用できる。
この場合は、補題 1 と (19) より、
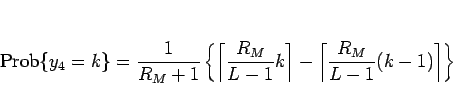
となる。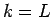 のときは、(19) より、
のときは、(19) より、
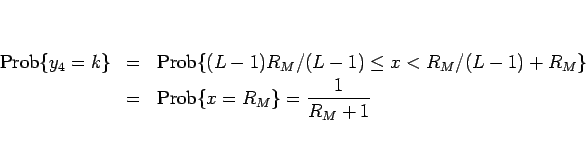
となるので、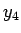 に関しては、
に関しては、
![\begin{displaymath}
\gamma_k
=
\left\{\begin{array}{cl}
\displaystyle \left\lce...
...right\rceil
& (1\leq k<L)\ [1zh]
1 & (k=L)\end{array}\right.\end{displaymath}](img105.gif)
に対して、
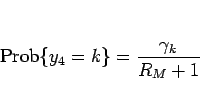
となることになる。
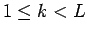 の場合は、補題 2 より
の場合は、補題 2 より
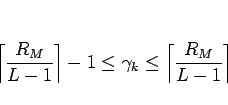 |
(20) |
であることがわかる。
これは、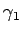 ,
,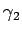 ,...,
,...,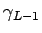 が
が 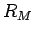 の
の
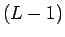 個への最適な均等配分であることを意味し、
よっていずれも
個への最適な均等配分であることを意味し、
よっていずれも
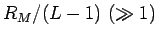 に近く、
に近く、
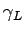 のみ 1 となっていることになる。
のみ 1 となっていることになる。
よって、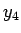 は、
は、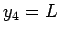 となる確率以外は均等だが、
となる確率以外は均等だが、
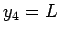 となる確率だけかなり小さい、ということになる。
となる確率だけかなり小さい、ということになる。
元々、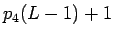 を考えてみれば、これは確かに
を考えてみれば、これは確かに
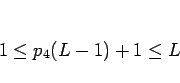
となり、それぞれの等号が成立する場合もあるのであるが、
この 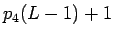 の整数部分 (
の整数部分 (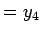 ) が
) が 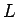 になるのは、
になるのは、
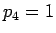 、すなわち
、すなわち 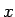 が丁度
が丁度 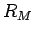 になるときのみであり、
それ以外の整数部分とは明らかに割合が違うことが想像できると思う。
になるときのみであり、
それ以外の整数部分とは明らかに割合が違うことが想像できると思う。
竹野茂治@新潟工科大学
2007年6月22日
![]() の場合は、補題 2 より
の場合は、補題 2 より
![]() ,
,![]() ,...,
,...,![]() が
が ![]() の
の
![]() 個への最適な均等配分であることを意味し、
よっていずれも
個への最適な均等配分であることを意味し、
よっていずれも
![]() に近く、
に近く、
![]() のみ 1 となっていることになる。
のみ 1 となっていることになる。
![]() は、
は、![]() となる確率以外は均等だが、
となる確率以外は均等だが、
![]() となる確率だけかなり小さい、ということになる。
となる確率だけかなり小さい、ということになる。
![]() を考えてみれば、これは確かに
を考えてみれば、これは確かに