4 y2 の一般の場合
この節では、3 節と同様にして、
一般の 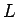 に対する
に対する 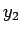 を考えてみることにする。
を考えてみることにする。
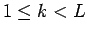 に対し、
に対し、
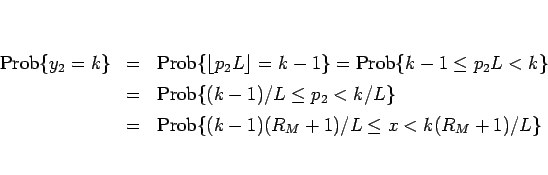
となり、
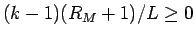 ,
,
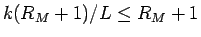 なので、
補題 1 により
なので、
補題 1 により
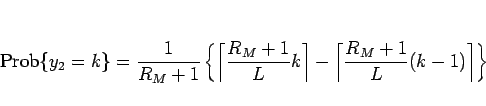 |
(15) |
となる。今、(15) の分子 (中カッコ内) を 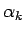 とすれば、
とすれば、
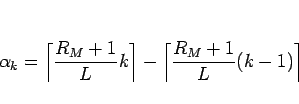 |
(16) |
となるが、これが 2 つの整数のいずれかとなることを示す。
補題 2
整数
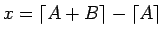 は、
は、
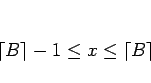
を満たし、よって、
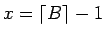 か
か
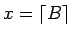 かの
いずれかである。
かの
いずれかである。
証明
今、任意の実数 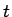 に対して
に対して
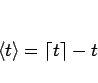
と書くことにすると、
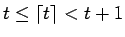 より
より
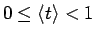 であり、よって、
であり、よって、
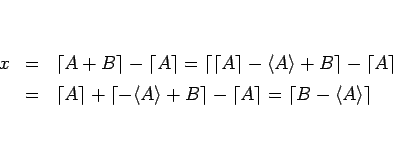
となる。よって、
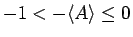 より、
より、
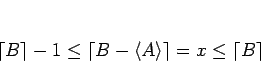
が言える。
この補題 2 と (16) より、
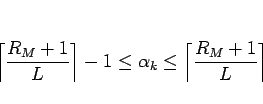 |
(17) |
であること、および、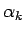 が
が
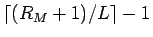 か
か
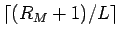 かの
いずれかであることがわかる。
かの
いずれかであることがわかる。
それは、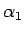 ,
,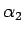 ,...,
,...,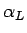 に、
高々 1 だけしか違いがないことを意味し、また、もちろん、
に、
高々 1 だけしか違いがないことを意味し、また、もちろん、
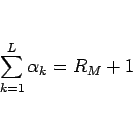
であるから、これらは、
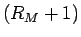 を
を 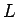 個へできるだけ均等に分割する方法として、
(16) の
個へできるだけ均等に分割する方法として、
(16) の 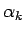 が
最適 (なものの一つ) であることを意味する。
が
最適 (なものの一つ) であることを意味する。
これにより、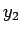 の妥当性の保証が得られたことになる。
の妥当性の保証が得られたことになる。
竹野茂治@新潟工科大学
2007年6月22日
![]() に対し、
に対し、
![]() は、
は、
![]() に対して
に対して
![]() ,
,![]() ,...,
,...,![]() に、
高々 1 だけしか違いがないことを意味し、また、もちろん、
に、
高々 1 だけしか違いがないことを意味し、また、もちろん、
![]() の妥当性の保証が得られたことになる。
の妥当性の保証が得られたことになる。