7 さらなる改善
4, 5 節の議論により、
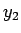 ,
, 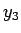 , そして
, そして 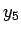 は同程度に確率を均等に配分していることが
わかったが、
は同程度に確率を均等に配分していることが
わかったが、
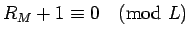 の場合は完全に均等で、
そうでなければ少しずれがあり、そのずれは
の場合は完全に均等で、
そうでなければ少しずれがあり、そのずれは
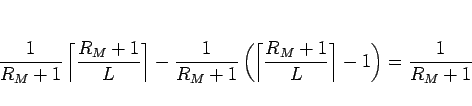 |
(21) |
である。通常この値は非常に小さいので、十分均等であると言える。
一方で、式 (18) で定義される  には
には
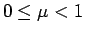 というパラメータが含まれ、
この値を変えると、
というパラメータが含まれ、
この値を変えると、
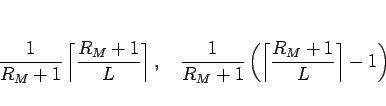
の現われ方が変わる。
よって、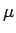 を定数とせず、
を定数とせず、
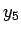 を使用する前に適当に取ってから
を使用する前に適当に取ってから 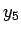 を使用すると、
適当にならされることでさらなる均等配分になることが期待される。
を使用すると、
適当にならされることでさらなる均等配分になることが期待される。
つまり、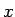 ,
, 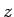 を、ともに rand() から独立に計算される乱数値、
すなわち 0 から
を、ともに rand() から独立に計算される乱数値、
すなわち 0 から 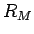 までの値を取る、独立で一様な確率変数とし、
までの値を取る、独立で一様な確率変数とし、
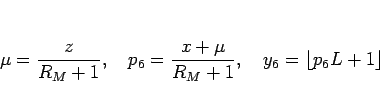 |
(22) |
と定められる 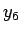 を考えてみる。
なお、この
を考えてみる。
なお、この 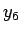 の計算には rand() を 2 回使用することになる。
の計算には rand() を 2 回使用することになる。
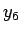 は
は 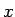 ,
, 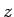 の 2 変数関数
の 2 変数関数 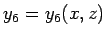 と考えることができ、
よって、
と考えることができ、
よって、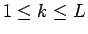 に対し、
に対し、
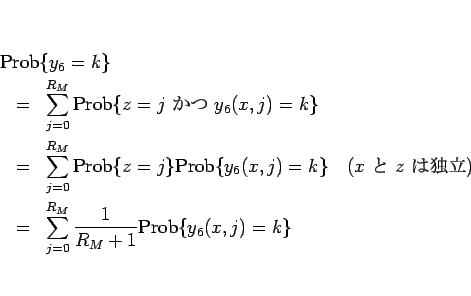
となるが、6 節と同様の計算により、
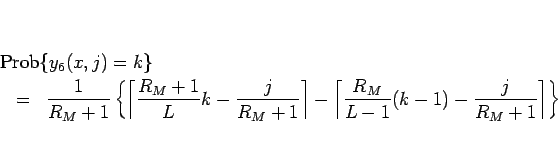
となるので、
となる。
補題 3
整数 A、および 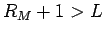 に対して、
に対して、
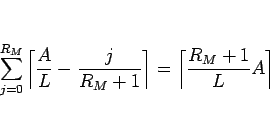 |
(25) |
証明
まず、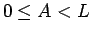 に対して (25) を示す。
このとき、
に対して (25) を示す。
このとき、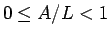 なので、
なので、
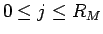 に対し、
に対し、
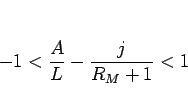
となる。よって、
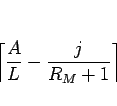
は、この場合 0 か 1 である。
よって、これが 1 となる 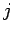 の個数を数えればよい。
これが 1 となるのは、
の個数を数えればよい。
これが 1 となるのは、
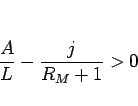
のとき、すなわち、
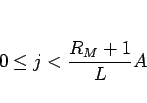
となる 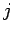 の個数となるので、
それは丁度
の個数となるので、
それは丁度
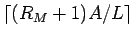 個となる。
よって、
個となる。
よって、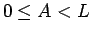 のときは (25) が成り立つ。
のときは (25) が成り立つ。
一般の整数 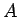 に対しては、
に対しては、
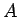 を
を 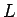 で割った商を
で割った商を 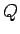 , 余りを
, 余りを 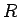 とすれば、
とすれば、
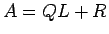 ,
, 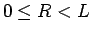 で、
で、
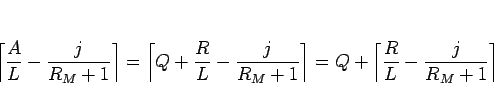
となり、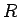 に対しては、
(25) の
に対しては、
(25) の 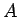 を
を 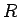 に変えたものが成り立つので、
に変えたものが成り立つので、
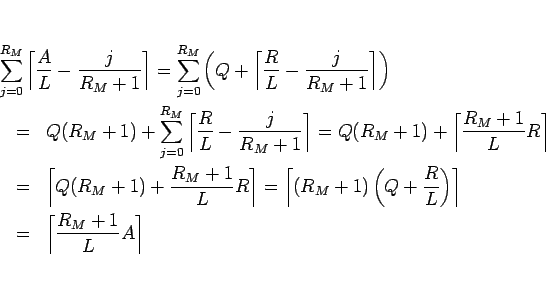
となり、一般の 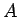 に対しても (25) が成り立つ。
に対しても (25) が成り立つ。
この補題 3 により、(24) は、
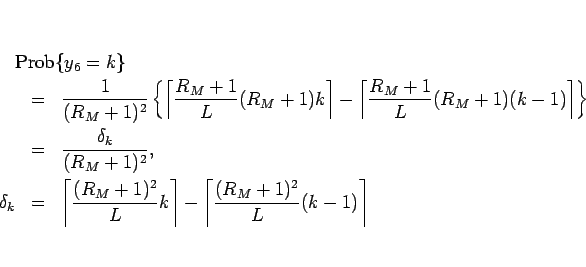
となる。この 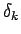 は、補題 2 により、
は、補題 2 により、
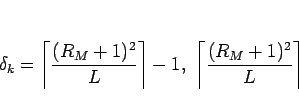
のいずれかであることもわかる。
よって、
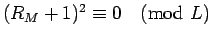 であれば、
であれば、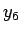 は均等で、
そうでない場合のずれは、
は均等で、
そうでない場合のずれは、
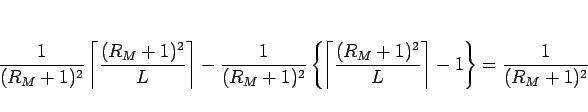
となり、(21) と比較すれば、
こちらの方がはるかに小さいことがわかる。
ついでに、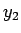 ,
, 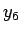 それぞれの分散も計算してみよう。
いずれも平均は
それぞれの分散も計算してみよう。
いずれも平均は 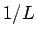 であるから、
であるから、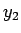 の分散
の分散 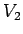 は、
は、
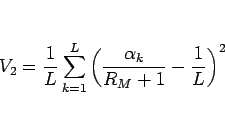 |
(26) |
と定義されるが、今、
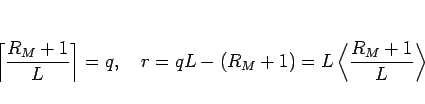
とすると、明らかに 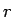 は
は 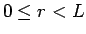 となる整数で、
となる整数で、
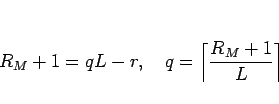 |
(27) |
となるので、この場合、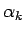 は、
は、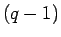 が
が 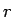 個、
個、
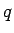 が
が 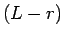 個あり、
個あり、
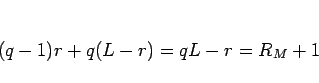
となっていることがわかる。よって、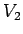 は、
は、
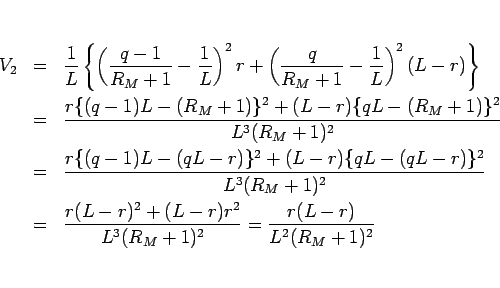
となる。
一方、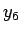 の分散
の分散 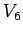 は、
は、
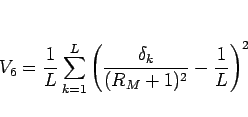
であり、この場合は、(27) の代わりに
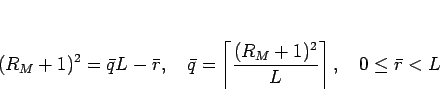 |
(28) |
と取れば、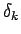 は、
は、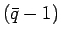 が
が 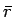 個、
個、
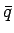 が
が 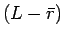 個あり、よって、
個あり、よって、
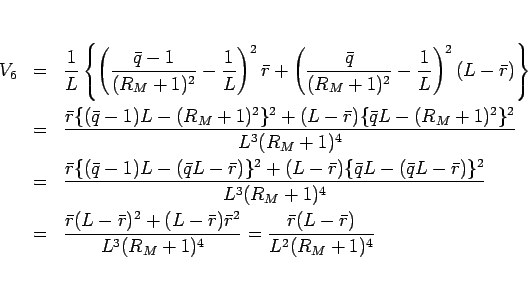
となる。
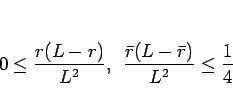
であり、もちろん 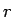 ,
, 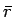 によって多少変わるが、
一般的には
によって多少変わるが、
一般的には  よりも
よりも 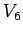 の方がかなり小さくなる。
の方がかなり小さくなる。
竹野茂治@新潟工科大学
2007年6月22日
![]() には
には
![]() というパラメータが含まれ、
この値を変えると、
というパラメータが含まれ、
この値を変えると、
![]() ,
, ![]() を、ともに rand() から独立に計算される乱数値、
すなわち 0 から
を、ともに rand() から独立に計算される乱数値、
すなわち 0 から ![]() までの値を取る、独立で一様な確率変数とし、
までの値を取る、独立で一様な確率変数とし、
![]() は
は ![]() ,
, ![]() の 2 変数関数
の 2 変数関数 ![]() と考えることができ、
よって、
と考えることができ、
よって、![]() に対し、
に対し、
![]() に対して、
に対して、
![]() に対して (25) を示す。
このとき、
に対して (25) を示す。
このとき、![]() なので、
なので、
![]() に対し、
に対し、
![]() に対しては、
に対しては、
![]() を
を ![]() で割った商を
で割った商を ![]() , 余りを
, 余りを ![]() とすれば、
とすれば、
![]() ,
, ![]() で、
で、
![]() ,
, ![]() それぞれの分散も計算してみよう。
いずれも平均は
それぞれの分散も計算してみよう。
いずれも平均は ![]() であるから、
であるから、![]() の分散
の分散 ![]() は、
は、
![]() の分散
の分散 ![]() は、
は、