![\includegraphics[height=6cm]{grv3-arcs1.eps}](img86.png)
|
まず、(a) は、対称軸を ![]() 軸と見れば、円弧の一部である
軸と見れば、円弧の一部である
![]() (
(
![]() ) の
) の ![]() 軸回りの
回転面なので、重心の
軸回りの
回転面なので、重心の ![]() 座標
座標 ![]() は (11) より
は (11) より
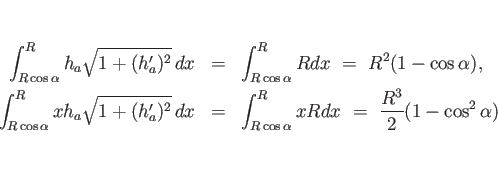
次は (b) であるが、これも同じ ![]() の下の図形の回転体なので、
(14) よりその重心の
の下の図形の回転体なので、
(14) よりその重心の ![]() 座標
座標 ![]() は、
は、
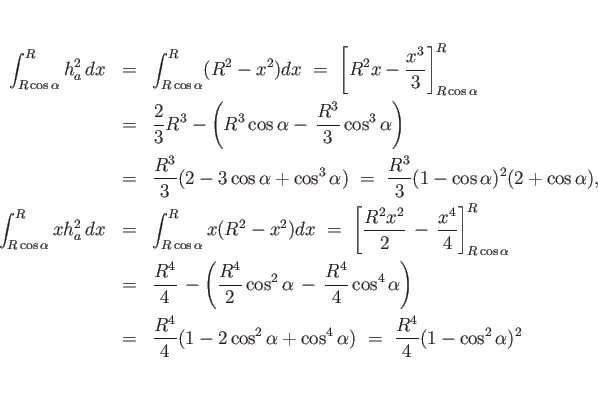
最後に (c) であるが、この計算は 2 通り考えられ、
一つは、一般的な公式 (9) に戻って、
その 3 重積分を 3 次元極座標変換して計算する方法である。
対称軸を ![]() 軸と見れば、(c) の積分領域は、
軸と見れば、(c) の積分領域は、
もう一つは、(c) を (b) と円錐に分離して考える方法であり、
それぞれの重心を求めた上で、
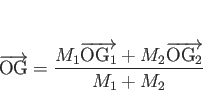
![\begin{displaymath}
h=h_c(x)
=
\left\{\begin{array}{ll}
x\tan\alpha & (0\leq x...
...]
\sqrt{R^2-x^2} & (R\cos\alpha\leq x\leq R)\end{array}\right.\end{displaymath}](img105.png)
![\begin{eqnarray*}\int_0^{R\cos\alpha}h_c(x)^2 dx
&=&
\left[\frac{x^3}{3}\tan^2...
...ht]_0^{R\cos\alpha}
=\
\frac{R^4}{4}\sin^2\alpha\cos^2\alpha\end{eqnarray*}](img110.png)
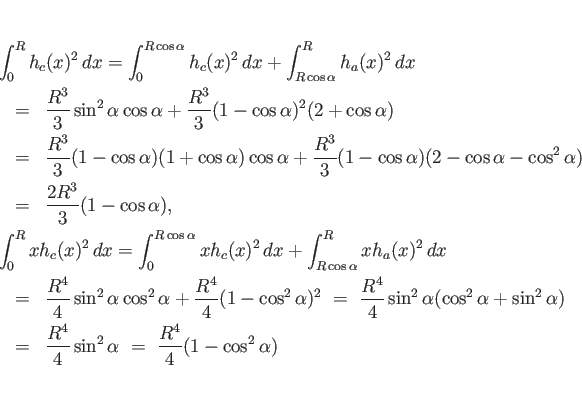
例えば、半球 (![]() ) の場合は
(20), (22), (24)
より
) の場合は
(20), (22), (24)
より ![]() ,
, ![]() となる。
球面よりも内部がつまっている球の方が赤道に近い部分が重い分、
重心が中心に近くなる。
また (20) より、
となる。
球面よりも内部がつまっている球の方が赤道に近い部分が重い分、
重心が中心に近くなる。
また (20) より、![]() は常に
は常に
![]() 座標の両端
座標の両端 ![]() ,
, ![]() の真ん中になるが、
これは 7 節で述べる写像の正積性とも関係する。
の真ん中になるが、
これは 7 節で述べる写像の正積性とも関係する。
(a),(b),(c) との比較の意味も込めて、
次はそれらの平面版である図形の重心を計算する。
すなわち、![]() は
は ![]() のグラフと
のグラフと ![]() のグラフをつなげた
図形の重心の
のグラフをつなげた
図形の重心の ![]() 座標、
座標、
![]() は
は ![]() のグラフから
のグラフから ![]() 軸までの領域の重心の
軸までの領域の重心の ![]() 座標、
座標、
![]() は
は ![]() のグラフから
のグラフから ![]() 軸までの領域の重心の
軸までの領域の重心の ![]() 座標
とする。こちらも密度はすべて一定とする。このとき、
座標
とする。こちらも密度はすべて一定とする。このとき、
![]() は、(15) より
は、(15) より
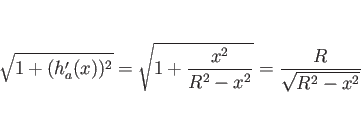
![\begin{eqnarray*}\int_{R\cos\alpha}^R\sqrt{1+(h_a'(x))^2} dx
&=&
\int_{R\cos\...
...rt{R^2-x^2}\right]_{R\cos\alpha}^R
[.5zh]
&=&
R^2\sin\alpha\end{eqnarray*}](img128.png)
![]() は、(17) より、
は、(17) より、
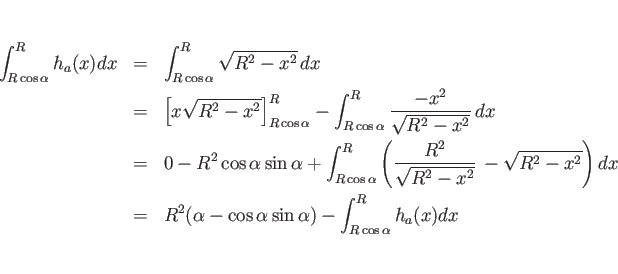
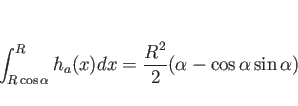
![\begin{eqnarray*}\int_{R\cos\alpha}^R xh_a(x)dx
&=&
\int_{R\cos\alpha}^Rx\sqrt...
...)^{3/2}\right]_{R\cos\alpha}^R
&=&
\frac{R^3}{3}\sin^3\alpha\end{eqnarray*}](img133.png)
最後に ![]() は、
(17) より、
は、
(17) より、
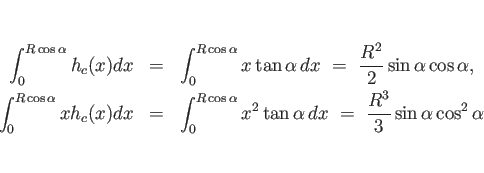
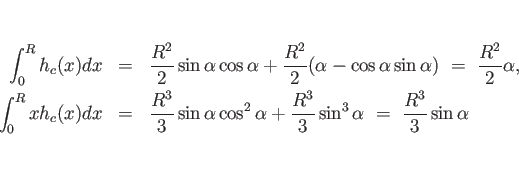
例えば半円 (![]() ) の場合、
) の場合、
![]() ,
,
![]() となる。
となる。
![]() ,
, ![]() ,
, ![]() はいずれも分母に
はいずれも分母に ![]() 自身が
残るため
自身が
残るため ![]() ,
, ![]() ,
, ![]() とはやや異なる。
平面と立体でこのような違いが現れるのは少し興味深い。
とはやや異なる。
平面と立体でこのような違いが現れるのは少し興味深い。
竹野茂治@新潟工科大学