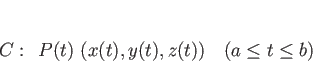
![]() 上定義された関数
上定義された関数
![]() に対して、
に対して、
![]() 上の
上の ![]() の線積分は、
の線積分は、
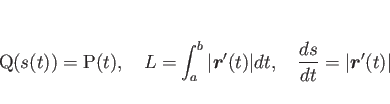
3 次元空間内の曲面 ![]() を、
を、![]() ,
, ![]() をパラメータとして、
をパラメータとして、
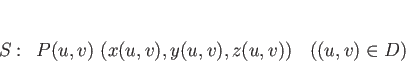
3 次元領域 ![]() 上で定義された関数
上で定義された関数
![]() に
対する
に
対する ![]() 上の体積分は、
上の体積分は、
次に、3 次元空間 (または 2 次元平面) 内の物体の重心の計算式を復習する。
曲線 ![]() が質量を持つ針金のようなものを表しているとき、
曲線上の点 P での線密度、すなわち長さ 1 あたりの
質量を
が質量を持つ針金のようなものを表しているとき、
曲線上の点 P での線密度、すなわち長さ 1 あたりの
質量を
![]() とすると、この
とすると、この ![]() の重心 G は
の重心 G は
同様に、質量を持つ曲面 ![]() の各点 P での面密度、
すなわち面積 1 あたりの質量を
の各点 P での面密度、
すなわち面積 1 あたりの質量を
![]() とすると、
その
とすると、
その ![]() の重心 G は
の重心 G は
また、質量を持つ 3 次元領域 ![]() の各点 P での密度、
すなわち体積 1 あたりの質量を
の各点 P での密度、
すなわち体積 1 あたりの質量を
![]() とすると、
その
とすると、
その ![]() の重心 G は
の重心 G は
竹野茂治@新潟工科大学