(10)、および (19) より、
![]() の回転体である
球面の
の回転体である
球面の ![]() の範囲の帯状領域の面積
の範囲の帯状領域の面積 ![]() は、
は、
なお、ここから、球の表面積は、その球と同じ半径で同じ高さの円筒の
面積
![]() と等しくなることもわかる。
と等しくなることもわかる。
この球からこの円筒、すなわち球に外接する同じ高さの円筒への、
中心軸から水平方向の射影
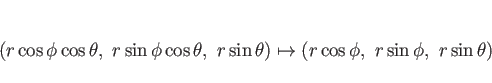
6 節で、![]() は
は ![]() の範囲の中心になっていたが、
これも、球面から円筒への射影が面積を変えないことからいえる。
つまり、この面積の不変性が、
図 2 の帯同士の重心の不変性も導き、
円筒上の帯の重心は当然
の範囲の中心になっていたが、
これも、球面から円筒への射影が面積を変えないことからいえる。
つまり、この面積の不変性が、
図 2 の帯同士の重心の不変性も導き、
円筒上の帯の重心は当然 ![]() の範囲の中心になるからである。
の範囲の中心になるからである。
ついでに、(31) のように、
曲線 ![]() の
の ![]() 軸に関する回転面
軸に関する回転面 ![]() の、
横幅
の、
横幅 ![]() に対する帯状部分の面積が、
場所によらずに
に対する帯状部分の面積が、
場所によらずに ![]() の定数倍になるための条件を考えてみよう。
の定数倍になるための条件を考えてみよう。
![]() であるとすると、
それに対する曲線
であるとすると、
それに対する曲線 ![]() 上の部分の長さ
上の部分の長さ ![]() は、
は、
![]() であり、
よって、その帯状部分の面積
であり、
よって、その帯状部分の面積 ![]() は、
は、
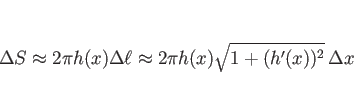
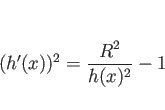
条件 (32) を図形的に解釈すると、
![]() はグラフの接線の傾きで、
その仰角を
はグラフの接線の傾きで、
その仰角を ![]() とすると (
とすると (
![]() )、
)、
![]() なので、
なので、
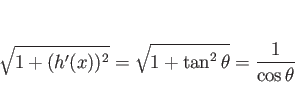
微分方程式 (33) を解いてみればわかるが、
それは ![]() 軸上に中心があり、半径
軸上に中心があり、半径 ![]() の円周のみと
なる (
の円周のみと
なる (
![]() )。
そのような円周の場合は、曲線上の点の法線は、
)。
そのような円周の場合は、曲線上の点の法線は、
![]() 軸上の中心で
軸上の中心で ![]() 軸と交わるので、
その距離は確かに常に半径
軸と交わるので、
その距離は確かに常に半径 ![]() に一致し一定となる。
逆にそうなる曲線はそのような円のみだということになる。
に一致し一定となる。
逆にそうなる曲線はそのような円のみだということになる。
なお、ついでに言えば、(33) を少し発展させ、
法線方向の ![]() 軸までの長さが
与えられた関数
軸までの長さが
与えられた関数 ![]() になるような微分方程式
になるような微分方程式
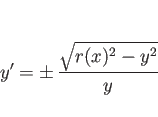
ここまでは、球面から円筒への射影の等積性を見てきたが、
良く知られているように、
球の体積にも円柱に関係する簡単な等積図形がある。
(b) で考察したような ![]() 軸のある範囲、
地球で言えばある緯度からある緯度までの球の体積は、
図 4 のような三角形
軸のある範囲、
地球で言えばある緯度からある緯度までの球の体積は、
図 4 のような三角形 ![]() を
を ![]() 軸の
まわりに回転させた図形、
すなわち球と同じ半径、同じ幅の円柱 (図 2 右) から、
半径
軸の
まわりに回転させた図形、
すなわち球と同じ半径、同じ幅の円柱 (図 2 右) から、
半径 ![]() 高さ
高さ ![]() の円錐を 2 つ取り除いた図形の
同じ幅の体積に一致する。
の円錐を 2 つ取り除いた図形の
同じ幅の体積に一致する。
それは、![]() 軸に垂直な面での両者の立体図形の断面積を比べればわかるが、
球の方の
軸に垂直な面での両者の立体図形の断面積を比べればわかるが、
球の方の ![]() での断面積は
での断面積は
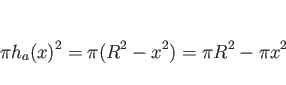
これにより、球面の場合と同様に、球のある ![]() 幅の重心は、
幅の重心は、
![]() の回転体の同じ幅の重心に一致するので、
そちらで置き換えて求めることもできる。
試しに、
の回転体の同じ幅の重心に一致するので、
そちらで置き換えて求めることもできる。
試しに、![]() をその考え方で計算してみよう。
をその考え方で計算してみよう。
まず、
![]() とし、
とし、
![]() の範囲での
の範囲での ![]() の
回転体の重心の
の
回転体の重心の ![]() 座標
座標 ![]() を考える。
これを、同じ範囲での半径
を考える。
これを、同じ範囲での半径 ![]() 、高さ
、高さ ![]() の円柱から、
半径
の円柱から、
半径 ![]() 、高さ
、高さ ![]() の円錐を取り除いたものと考え、
円柱の重心の
の円錐を取り除いたものと考え、
円柱の重心の ![]() 座標
座標 ![]() と
円錐の重心の
と
円錐の重心の ![]() 座標
座標 ![]() で表せば、
で表せば、
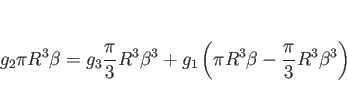
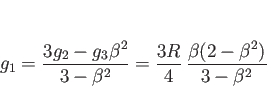
一方、半球に対応する ![]() の範囲での
の範囲での ![]() の
回転体は、
の
回転体は、
![]() が 1 の場合に対応するので、
その重心の
が 1 の場合に対応するので、
その重心の ![]() 座標
座標 ![]() は
は
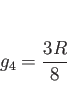
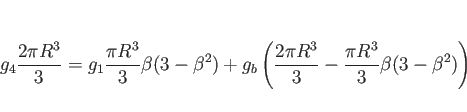
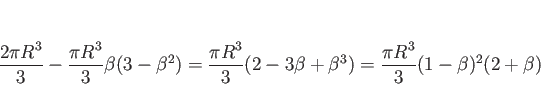
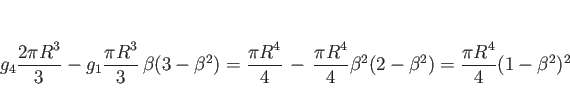
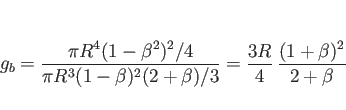
竹野茂治@新潟工科大学