7.2 エントロピー条件
最後に、エントロピー条件 (2.3) を考える。
7.1 節と同様にして、
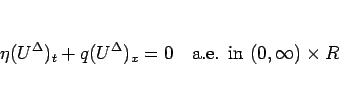
であるので、
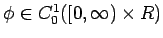 ,
, 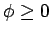 に対し、
に対し、
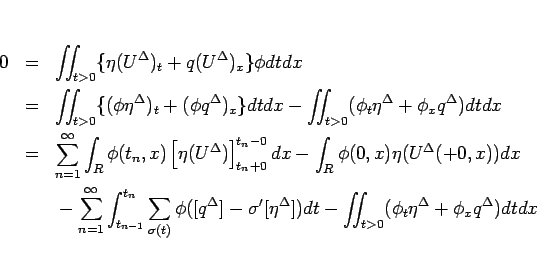
ここで、[竹野] にあるように、不連続波に対する
![$[q^\Delta]-\sigma'[\eta^\Delta]$](img744.gif) の値は、
の値は、
- 衝撃波に対しては
![$[q^\Delta]-\sigma'[\eta^\Delta]\leq 0$](img745.gif)
- 接触不連続に対しては
![$[q^\Delta]-\sigma'[\eta^\Delta]=0$](img746.gif)
であるので、
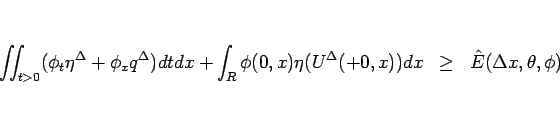
が言えることになる。ここで、
![\begin{displaymath}
\hat{E}(\Delta x,\theta,\phi)
=\sum_{n=1}^\infty\int_R\phi(t_n,x)
\left[\eta^\Delta\right]^{t_n-0}_{t_n+0}dx
\end{displaymath}](img748.gif)
である。
今、 を
を
 と取れば、
7.1 節と同様にして、
と取れば、
7.1 節と同様にして、
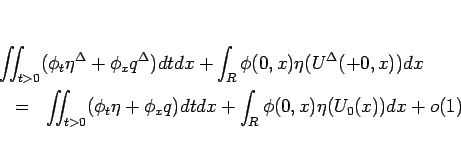
であることが言えるから、よって後は
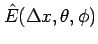 が 0 になるようにすればよい。
しかし、これに対しては、
が 0 になるようにすればよい。
しかし、これに対しては、
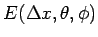 と全く同じ議論を繰り返すことにより、
と全く同じ議論を繰り返すことにより、
 の部分列
の部分列
 と、
と、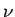 に関する 0 集合
に関する 0 集合 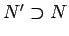 が取れて、
が取れて、
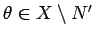 に対し、
任意の
に対し、
任意の
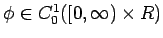 に対して
に対して
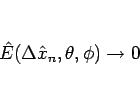
となることを言うことができる。
よって、その
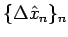 と
と
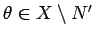 に対する極限は、
弱解でかつエントロピー条件
に対する極限は、
弱解でかつエントロピー条件
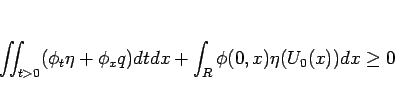 |
(7.116) |
を満たすことが言える (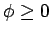 )。
なお、この (7.19) は、初期値の項がついているので、
その分だけ (2.3) よりも強い条件になっている
が、もちろん (2.3) も成立する。
)。
なお、この (7.19) は、初期値の項がついているので、
その分だけ (2.3) よりも強い条件になっている
が、もちろん (2.3) も成立する。
定理 7.2
定理 5.1 の仮定の下で構成した
Glimm 差分近似解 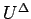 に対し、
0 に収束する列
に対し、
0 に収束する列
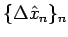 と
と
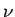 に関する 0 集合
に関する 0 集合 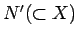 が存在して、
が存在して、
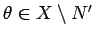 に対する
に対する
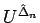 の極限は、エントロピー条件 (7.19) を満たす弱解であり、
(6.9), (6.10),
(6.11) を満たす。
の極限は、エントロピー条件 (7.19) を満たす弱解であり、
(6.9), (6.10),
(6.11) を満たす。
竹野茂治@新潟工科大学
2009年1月18日
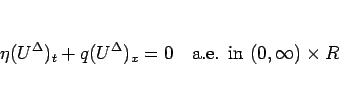
![]() を
を
![]() と取れば、
7.1 節と同様にして、
と取れば、
7.1 節と同様にして、
![]() と
と
![]() に対する極限は、
弱解でかつエントロピー条件
に対する極限は、
弱解でかつエントロピー条件
![]() に対し、
0 に収束する列
に対し、
0 に収束する列
![]() と
と
![]() に関する 0 集合
に関する 0 集合 ![]() が存在して、
が存在して、
![]() に対する
に対する
![]() の極限は、エントロピー条件 (7.19) を満たす弱解であり、
(6.9), (6.10),
(6.11) を満たす。
の極限は、エントロピー条件 (7.19) を満たす弱解であり、
(6.9), (6.10),
(6.11) を満たす。