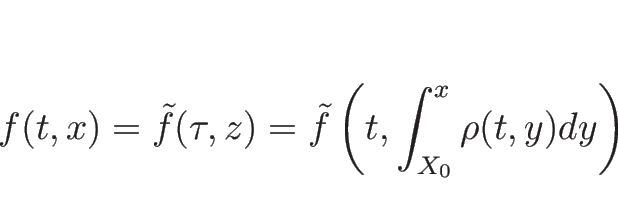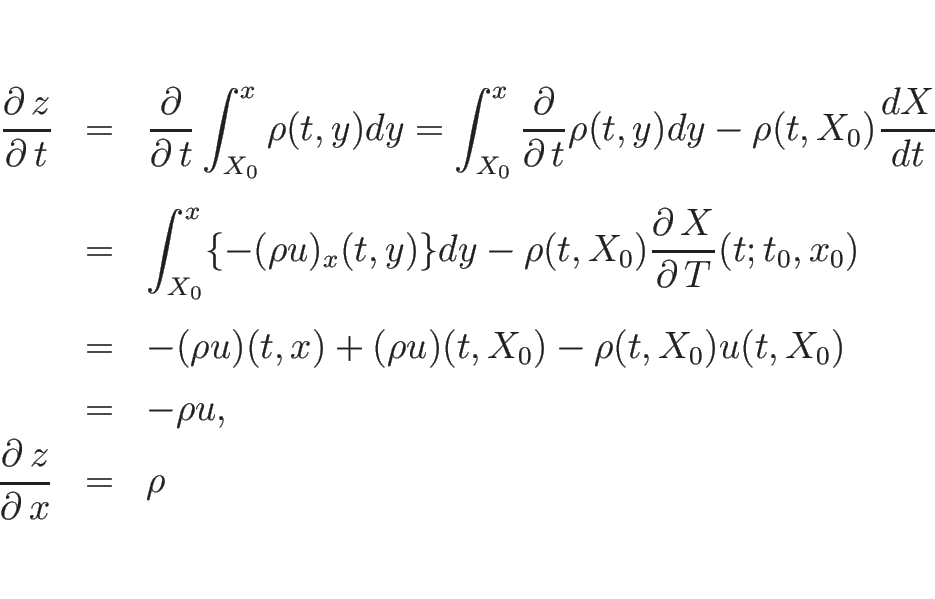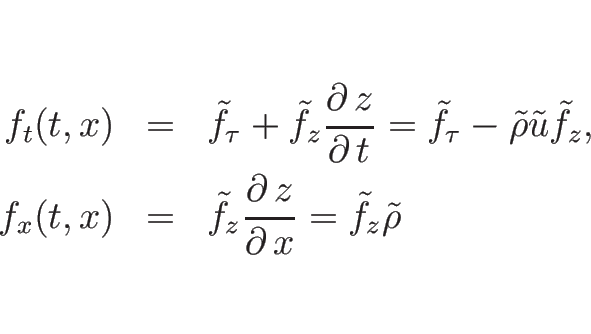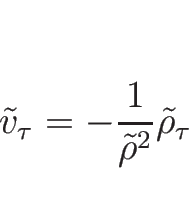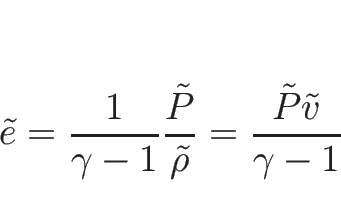2.6 ラグランジュ座標系
2.4, 2.5 節で
導いた保存則方程式は、固定座標系、いわゆるオイラー座標系での
理想気体の保存則方程式であるが、
流体の動きに付随する動座標系、いわゆるラグランジュ座標系での
考察もよく行われていて、特に 1 次元の気体の方程式に対しては、
質量座標系 という動座標系を使うと形が綺麗になることが知られていて、
ここではそれを紹介する。
質量座標とは、単に流体の運動に付随する動座標 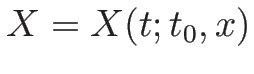 を
を
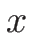 の代わりに用いるのではなく、
ある基準となる流体位置
の代わりに用いるのではなく、
ある基準となる流体位置
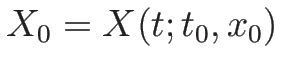 から
から 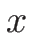 までの質量
までの質量
![$M^1_{[X_0,x]}(t)$](img146.png) を空間座標として用いることをいう。
すなわち、
を空間座標として用いることをいう。
すなわち、
を 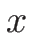 の代わりの空間座標とすることになる。
の代わりの空間座標とすることになる。
なので、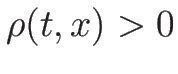 であれば各
であれば各 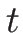 に対して
に対して 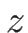 は
は
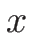 の単調増加関数、すなわち 1 対 1 に対応することとなり、
の単調増加関数、すなわち 1 対 1 に対応することとなり、
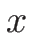 の代わりに
の代わりに 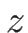 を新たな座標系と取ることができる。
つまり、
を新たな座標系と取ることができる。
つまり、
として 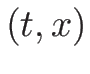 の代わりに
の代わりに 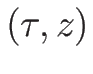 を座標系として考えるのが
質量座標系である。
を座標系として考えるのが
質量座標系である。
今、質量座標系で 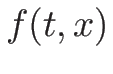 が
が
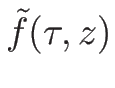 と表されるとすると
(以後、
と表されるとすると
(以後、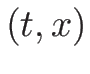 の関数を
の関数を 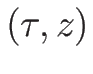 の関数と見る場合は
このように
の関数と見る場合は
このように 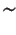 をつけて書き表すこととする)、
をつけて書き表すこととする)、
であり、(2.5), (2.10)
より、
となるので、
となる。これを、各保存則に適用すると、
となる。(2.18) を保存形にするために
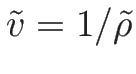 とすると、
とすると、
より、質量座標系による保存則方程式系
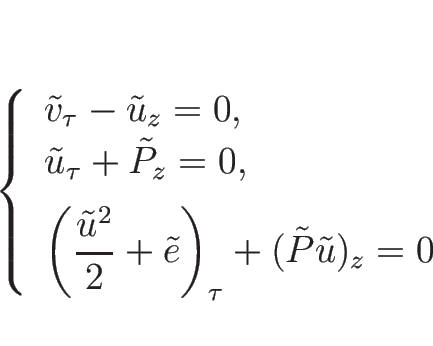 |
(2.19) |
が得られることになる。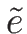 は、
は、
であるが、バロトロピー、すなわち 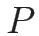 が
が 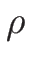 のみの関数であるとすれば、
のみの関数であるとすれば、
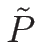 は
は 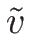 のみの関数となり、
等エントロピー流であれば
のみの関数となり、
等エントロピー流であれば
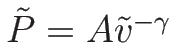 、
等温流であれば
、
等温流であれば
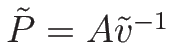 のようになって、
(2.19) の最初の 2 本のみで閉じた方程式系となる。
この場合この 2 本からなる保存則方程式系を、
特に
のようになって、
(2.19) の最初の 2 本のみで閉じた方程式系となる。
この場合この 2 本からなる保存則方程式系を、
特に 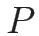 -system と呼ぶことがある。
-system と呼ぶことがある。
竹野茂治@新潟工科大学
2018-08-01
![]() を
を
![]() の代わりに用いるのではなく、
ある基準となる流体位置
の代わりに用いるのではなく、
ある基準となる流体位置
![]() から
から ![]() までの質量
までの質量
![]() を空間座標として用いることをいう。
すなわち、
を空間座標として用いることをいう。
すなわち、
![\begin{eqnarray*}z
&=&
z(t,x)
=
\left\{\begin{array}{ll}
M^1_{[X_0,x]}(t) ...
... &=&
\bar{M}^1(t,x)-\bar{M}^1(t,X_0)
=
\int_{X_0}^x\rho(t,y)dy\end{eqnarray*}](img147.png)
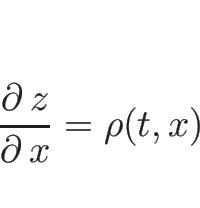
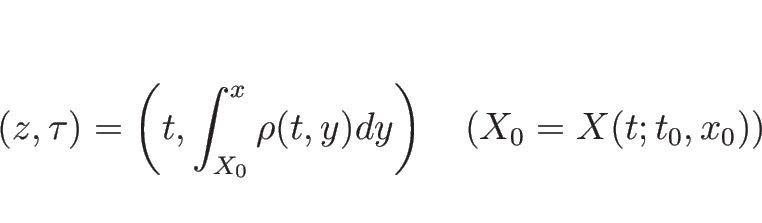
![]() が
が
![]() と表されるとすると
(以後、
と表されるとすると
(以後、![]() の関数を
の関数を ![]() の関数と見る場合は
このように
の関数と見る場合は
このように ![]() をつけて書き表すこととする)、
をつけて書き表すこととする)、