速度 ![]() に対しては位置の移動が局所化の前の量であり、
時刻が
に対しては位置の移動が局所化の前の量であり、
時刻が ![]() のときに
のときに ![]() にあった気体の
にあった気体の ![]() での位置を
での位置を
![]() と書くことにすると、
と書くことにすると、
![]() であり、
また任意の
であり、
また任意の
![]() に対して、
に対して、
速度 ![]() は、位置の時間に関する微分であるから、
は、位置の時間に関する微分であるから、
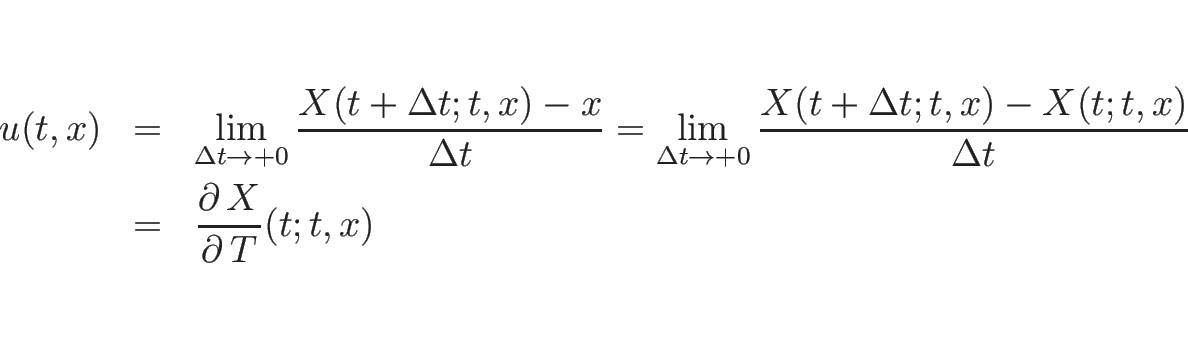
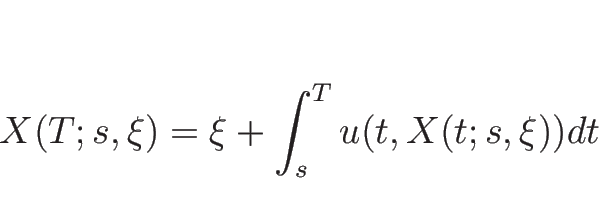
さて、今 ![]() に対して
に対して ![]() 、
すなわち
、
すなわち ![]() のときに
のときに ![]() にあった気体が
にあった気体が
![]() のときにいる位置を
のときにいる位置を ![]() とすると、
とすると、
![]() をこの間に通過した質量
をこの間に通過した質量
![]() は、
は、
![]() のときに
のときに ![]() から
から ![]() までの間に存在する
気体の質量に等しい。よって、
までの間に存在する
気体の質量に等しい。よって、
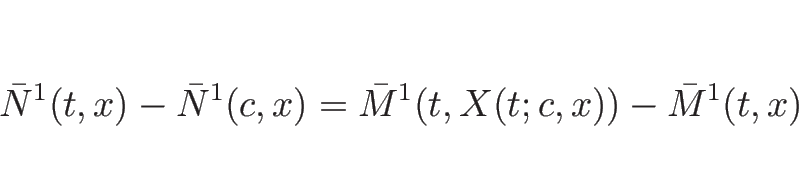
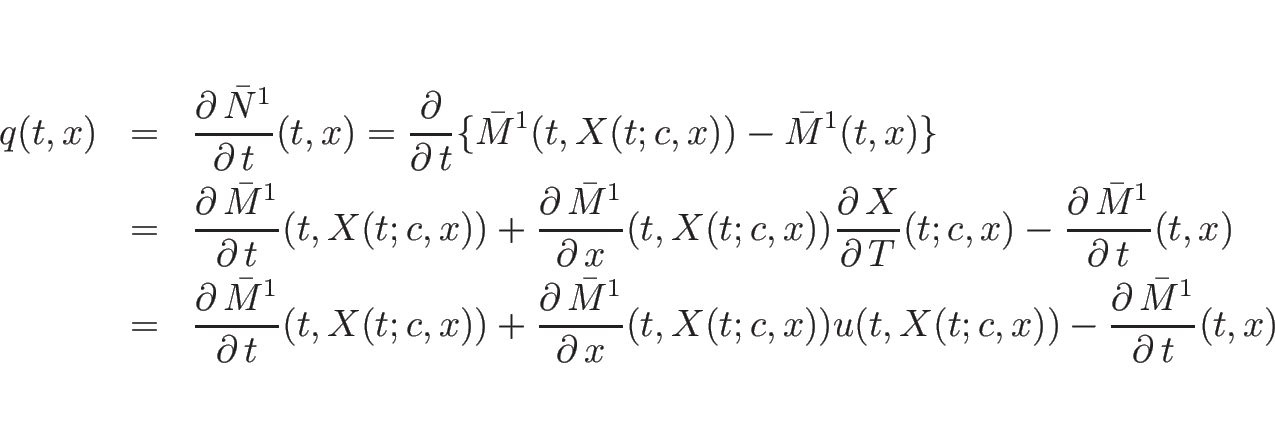
竹野茂治@新潟工科大学