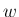 の不等式の方だけ考えれば良いことを先に示す。
の不等式の方だけ考えれば良いことを先に示す。
まず、定理 2 の (22) は 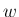 の不等式の方だけ考えれば良いことを先に示す。
の不等式の方だけ考えれば良いことを先に示す。
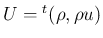 に対して、
速度の符号を反対にしたものを
に対して、
速度の符号を反対にしたものを
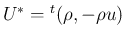 のように
書くことにする。このとき、容易に
のように
書くことにする。このとき、容易に
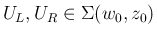 のときは、
のときは、
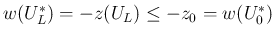 等より
等より
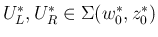 であり、
(17) より
であり、
(17) より
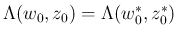 も
いえるので、
よって、もし定理 2 の (22) の
も
いえるので、
よって、もし定理 2 の (22) の 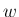 に
関する不等式が成り立てば、
それを
に
関する不等式が成り立てば、
それを
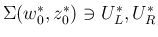 に
適用すると
に
適用すると
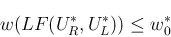
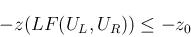
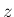 に関する不等式が
得られる。よって以後
に関する不等式が
得られる。よって以後 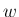 の方のみ考える。
の方のみ考える。
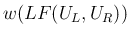 は、
は、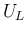 ,
, 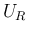 が領域
が領域
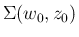 を
動く 4 変数関数と見ることができるが、
まずは一方を固定して 2 変数関数として考える。
を
動く 4 変数関数と見ることができるが、
まずは一方を固定して 2 変数関数として考える。
以後、
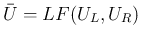 とし、
とし、
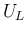 ,
, 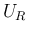 ,
, 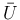 を
を 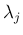 や
や 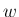 等に代入したものを、
それぞれ
等に代入したものを、
それぞれ 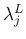 ,
, 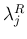 ,
,
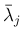 ,
,
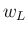 ,
, 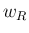 ,
, 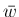 のようにも書くこととする。
のようにも書くこととする。
まず、
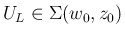 を固定し、
を固定し、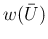 を
を 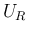 に
関する 2 変数関数とみて、その停留点を求めてみる。
に
関する 2 変数関数とみて、その停留点を求めてみる。
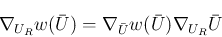
![\begin{eqnarray*}\nabla_U w(U)
&=&
\left(\frac{\partial w}{\partial \rho}, \f...
...R\lambda_2^R & \mu - \lambda_1^R-\lambda_2^R
\end{array} \right]\end{eqnarray*}](img205.png)
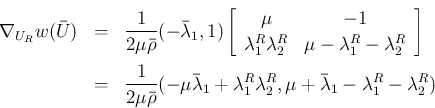
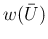 の
の 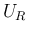 に関する停留点があるとすると、
そこで
に関する停留点があるとすると、
そこで
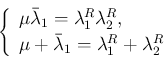
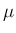 ,
,
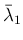 が 2 次方程式
が 2 次方程式
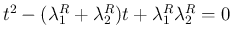 の解
であることを意味し、よって
の解
であることを意味し、よって
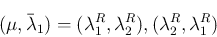
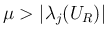 なので、これらはいずれも成立しない。
つまり、
なので、これらはいずれも成立しない。
つまり、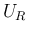 に関する停留点は存在しない。
に関する停留点は存在しない。
よって、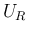 を動かした場合、
を動かした場合、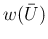 はその最大値を
領域
はその最大値を
領域
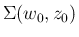 の内部で取ることはない。
の内部で取ることはない。
同様に
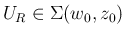 を固定して
を固定して 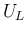 に関する停留点を考えると、
に関する停留点を考えると、
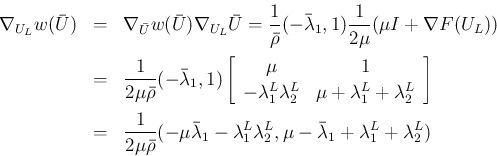
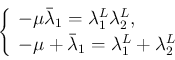
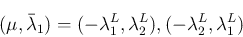
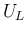 を動かした場合の停留点も存在しない。
を動かした場合の停留点も存在しない。
よって、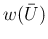 は
は 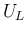 に関する最大値を領域
に関する最大値を領域
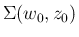 の
内部では取らない。
の
内部では取らない。
これらにより、4 変数関数 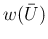 の最大値は、
の最大値は、
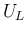 ,
, 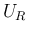 の両方が領域
の両方が領域
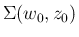 の境界上にあるときに
取ることがわかる。
の境界上にあるときに
取ることがわかる。
竹野茂治@新潟工科大学