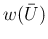
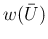 の、
の、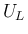 ,
, 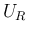 が
が
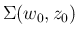 の境界上を動くときの最大値を考える。
の境界上を動くときの最大値を考える。
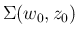 の境界は、
の境界は、
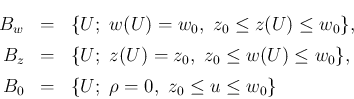
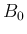 を
除外しておく。
を
除外しておく。
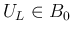 の場合は、
の場合は、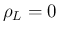 より、
より、
![\begin{displaymath}
U_L = \left[\begin{array}{c}\rho_L\\ \rho_L u_L\end{array}\r...
...y}{c}\rho_L u_L\\ \rho_L u_L^2+P(\rho_L)\end{array}\right] = 0
\end{displaymath}](img220.png)
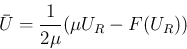
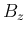 の端 (
の端 (
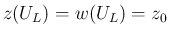 )、
および
)、
および  の端 (
の端 (
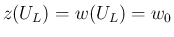 ) でも同じなので、
それらに含まれると考えてよい。
) でも同じなので、
それらに含まれると考えてよい。
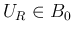 の場合も同様なので、
よって、
の場合も同様なので、
よって、
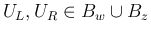 としてよいことになる。
としてよいことになる。
今後、
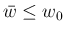 であることを示す代わりに、
であることを示す代わりに、
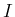 が 0 以上になるかどうかを考えることにする。
まず
が 0 以上になるかどうかを考えることにする。
まず 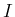 を変形する。
を変形する。
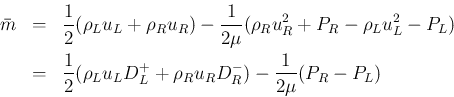
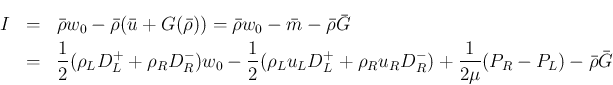
まず、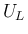 を
を 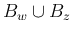 上に固定して、
上に固定して、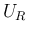 を
を 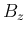 上で
動かして考える。この場合、
上で
動かして考える。この場合、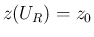 より
より
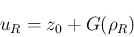
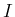 は
は 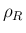 の 1 変数関数と見ることができる。
その
の 1 変数関数と見ることができる。
その 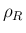 に関する導関数を計算する。
に関する導関数を計算する。
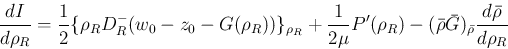
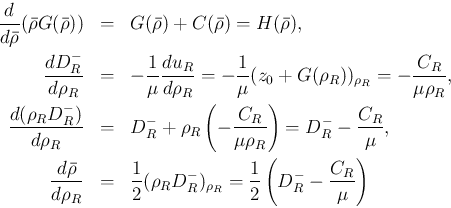
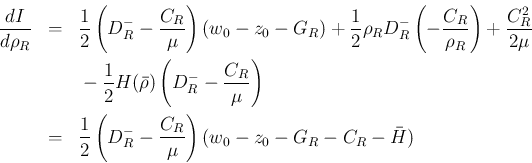
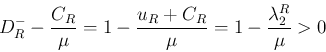
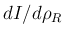 の符号は
の符号は
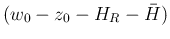 の符号に等しい。
の符号に等しい。
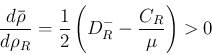
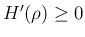 より
より 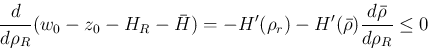
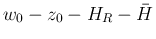 は
は 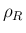 に関して非増加関数となる。
よって、(29) の右辺は正の値と非増加関数の積なので、
常に負か、常に正か、またはあるところまでは正であるところから負、
の 3 通りのうちのいずれかとなり、
に関して非増加関数となる。
よって、(29) の右辺は正の値と非増加関数の積なので、
常に負か、常に正か、またはあるところまでは正であるところから負、
の 3 通りのうちのいずれかとなり、
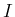 はそれぞれ単調減少、単調増加、または増加して減少する関数となるから、
いずれの場合でもその最小値は両端の
はそれぞれ単調減少、単調増加、または増加して減少する関数となるから、
いずれの場合でもその最小値は両端の 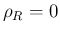 ,
, 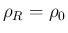 の
いずれかで取ることになる。
の
いずれかで取ることになる。
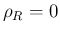 の場合は、
の場合は、 に含まれ、
それはどこでも値は変わらなかったので、
結局その端の値は
に含まれ、
それはどこでも値は変わらなかったので、
結局その端の値は  の端での値と同じになるから、
結局
の端での値と同じになるから、
結局
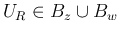 での
での  の最小値は、
の最小値は、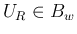 での最小値
に等しい。
での最小値
に等しい。
よって次は、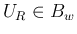 を固定して、
を固定して、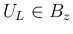 を動かして
その最小値を考える。この場合は、
を動かして
その最小値を考える。この場合は、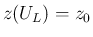 より
より
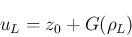
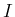 に代入すれば
に代入すれば 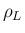 の 1 変数関数となり、
それを
の 1 変数関数となり、
それを 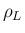 で微分する。この場合、
で微分する。この場合、
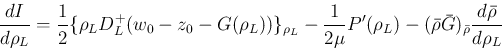
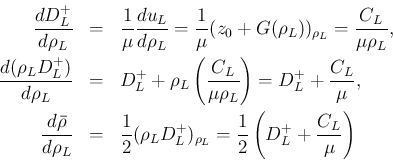
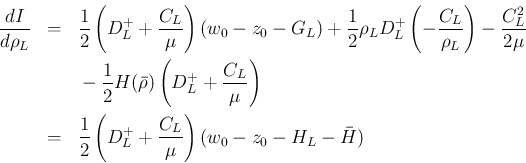
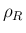 の場合同様、CFL 条件により
の場合同様、CFL 条件により
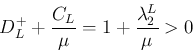
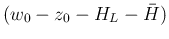 も
も 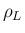 に関して非増加となるので、
に関して非増加となるので、
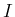 の最小値は両端
の最小値は両端 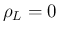 ,
, 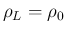 で取る。
よって、
で取る。
よって、
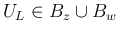 での
での 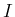 の最小値は
の最小値は 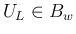 の最小値に等しくなる。
の最小値に等しくなる。
以上により、
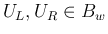 での最小値を考えればよいことになる。
での最小値を考えればよいことになる。
最後に、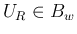 に固定したまま、
に固定したまま、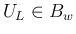 を動かして
考える。この場合は
を動かして
考える。この場合は 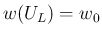 より
より
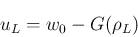
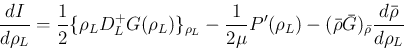
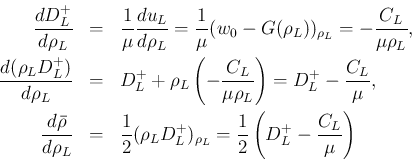
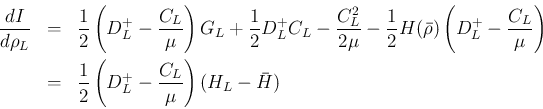
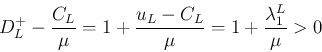
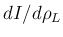 の符号は
の符号は 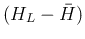 の符号に等しく、
の符号に等しく、
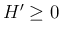 よりそれは
よりそれは
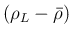 の符号に等しい。
の符号に等しい。
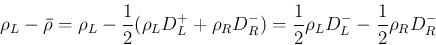
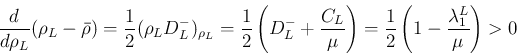
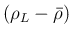 は増加関数。
は増加関数。
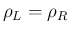 のときは、
のときは、
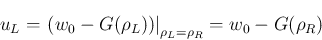
 より
より  なので
なので
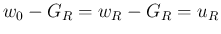 、
よって
、
よって 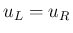 となるから、
となるから、
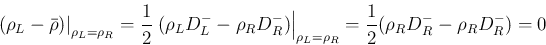
 は
は  で符号を変え、
で符号を変え、
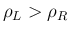 ならば正、
ならば正、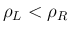 ならば負となる。
ならば負となる。
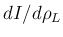 の符号はその符号に等しいので、
よって
の符号はその符号に等しいので、
よって 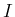 は
は
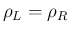 で最小値を取る。
で最小値を取る。
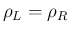 のときは
のときは 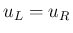 なので、
なので、
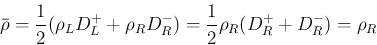
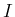 の最小値は
の最小値は
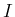 の最小値が 0 であることがわかり、
の最小値が 0 であることがわかり、
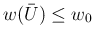 が示されたことになる。
が示されたことになる。
竹野茂治@新潟工科大学