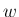
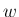 ,
, 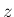 に対して、後で「不変領域」として使用する
次のような領域を考える。
なお、本稿ではこの
に対して、後で「不変領域」として使用する
次のような領域を考える。
なお、本稿ではこの 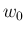 ,
, 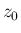 は、
ある
は、
ある 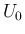 に対して
に対して 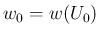 ,
, 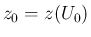 であるもののみを考える。
であるもののみを考える。
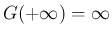 であれば任意の
であれば任意の 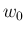 ,
, 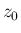 (
(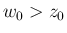 ) に
対してそのような
) に
対してそのような 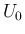 が常にみつかるが、
が常にみつかるが、
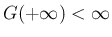 の場合はそうとは限らないことに注意せよ (本稿では、
の場合はそうとは限らないことに注意せよ (本稿では、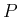 に関する条件として
に関する条件として
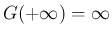 は仮定していない)。
は仮定していない)。
領域
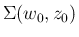 に
に 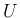 が入る条件は、
が入る条件は、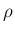 ,
, 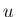 で考えると
で考えると
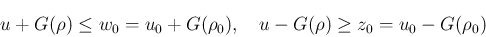
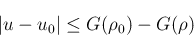
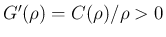 (
( ) なので、
この不等式は
) なので、
この不等式は
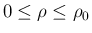 の範囲のみで意味を持ち、
よって (14) は
と書くこともできる。
この領域は、
の範囲のみで意味を持ち、
よって (14) は
と書くこともできる。
この領域は、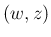 ,
, 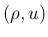 ,
, 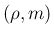 の座標軸では、それぞれ
図 1
の座標軸では、それぞれ
図 1 3 のように
なる (厳密な図ではなく、おおよその図)。
これらの図からもわかるが、
3 のように
なる (厳密な図ではなく、おおよその図)。
これらの図からもわかるが、
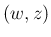 ,
, 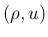 座標系での
座標系での 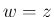 、すなわち
、すなわち 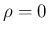 上の線分は、
本来の
上の線分は、
本来の 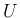 である
である 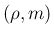 座標系では原点 1 点に対応することに
注意する。
座標系では原点 1 点に対応することに
注意する。
今、この領域
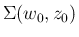 での固有値の絶対値の上限を、
での固有値の絶対値の上限を、
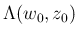 と書くことにする:
と書くことにする:
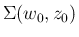 での
での
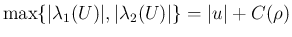 の最大値は、
の最大値は、
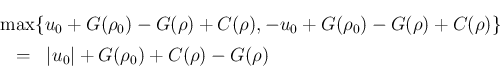
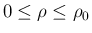 での最大値に等しく、
よって
での最大値に等しく、
よって
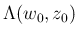 は
となることがわかる。例えば
は
となることがわかる。例えば
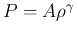 ,
, 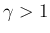 (等エントロピー) の場合は、
(等エントロピー) の場合は、
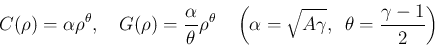
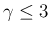 ならば
ならば
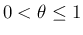 より
より
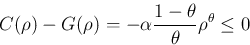
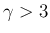 ならば
ならば 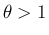 より
より
![\begin{displaymath}
C(\rho)-G(\rho) = \alpha\frac{\theta-1}{\theta}\rho^\theta
\in [0,C(\rho_0)-G(\rho_0)]
\end{displaymath}](img113.png)
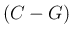 は単調とは限らず、
よって、(17) は (18), (19) のような易しい式
になるとは限らない。
は単調とは限らず、
よって、(17) は (18), (19) のような易しい式
になるとは限らない。
最後に、6 節で利用する以下の性質を示しておく。
は、
の座標系では凸図形、すなわち、
で、証明は下に凸、
は上に凸。
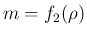 は
は 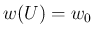 なので、
なので、
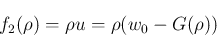
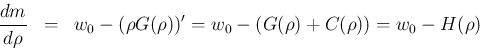
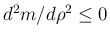 だから
この曲線は上に凸となる。
だから
この曲線は上に凸となる。
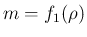 も
も 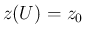 なので、
なので、
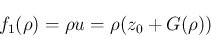
竹野茂治@新潟工科大学