5 不偏分散の自乗の展開

本節では (7) を示すために、不偏分散の分散 (確率変数としての分散) を計算する。

(6) より、

$\begin{displaymath} V[V_1] = E[(V_1-\sigma^2)^2] = E[V_1^2]-(\sigma^2)^2\end{displaymath}$ (9)

であるが、この

は (2) より、

$\begin{displaymath} E[V_1^2] = E\left[\left(\frac{n}{n-1}\right)^2 (\overlin... ...overline{X^2}^2-2\overline{X^2}\,\overline{X}^2+\overline{X}^4]\end{displaymath}$ (10)

となる。この (10) の最後の式の中身を順に展開していくが、そのために次のような記号を導入する。 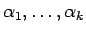$\alpha_1,\ldots,\alpha_k$ を自然数として、

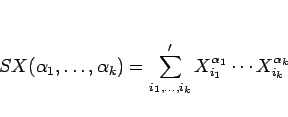$\begin{displaymath} SX(\alpha_1,\ldots,\alpha_k) = \sum'_{i_1,\ldots,i_k}X_{i_1}^{\alpha_1}\cdots X_{i_k}^{\alpha_k}\end{displaymath}$ (11)

と定義する。ただし、和 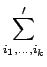$\displaystyle \sum'_{i_1,\ldots,i_k}$ は、各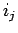

が 1 から

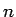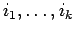まで動き、かつ $i_1,\ldots,i_k$ はすべて互いに異なるものに対する和であるとする。例えば、

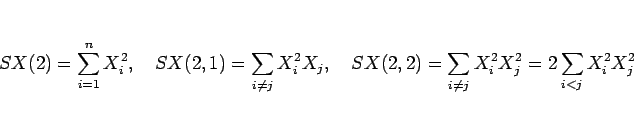
$\begin{displaymath} SX(2) = \sum_{i=1}^nX_i^2, \hspace{1zw} SX(2,1) = \sum_{i\ne... ...zw} SX(2,2) = \sum_{i\neq j}X_i^2X_j^2 = 2\sum_{i<j}X_i^2X_j^2 \end{displaymath}$

などとなる。

命題 2

同士の積について次が成り立つ。

	$\displaystyle {SX(\alpha_1,\ldots,\alpha_k)SX(\beta) }$
		$\textstyle =$	$\displaystyle \sum_{j=1}^k SX(\alpha_1,\ldots,\alpha_j+\beta,\ldots,\alpha_k) + SX(\alpha_1,\ldots,\alpha_k,\beta)$	(12)

証明

(12) の左辺は、

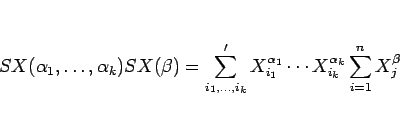
$\begin{displaymath} SX(\alpha_1,\ldots,\alpha_k)SX(\beta) = \sum'_{i_1,\ldots... ...}^{\alpha_1}\cdots X_{i_k}^{\alpha_k} \sum_{i=1}^n X_j^\beta \end{displaymath}$

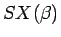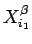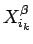であるが、 $SX(\beta)$ の部分を $X_{i_1}^\beta$ , ..., $X_{i_k}^\beta$ と、それ以外に分ければ、

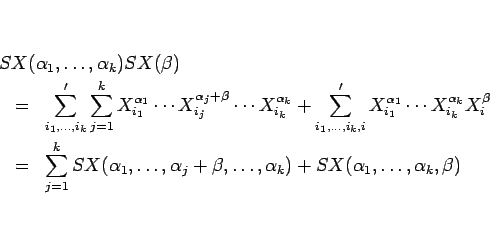
$\begin{eqnarray*}\lefteqn{SX(\alpha_1,\ldots,\alpha_k)SX(\beta) } \\ &=& \sum'... ..._j+\beta,\ldots,\alpha_k) + SX(\alpha_1,\ldots,\alpha_k,\beta) \end{eqnarray*}$

これを使うと、まず 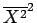$\overline{X^2}^2$ は、

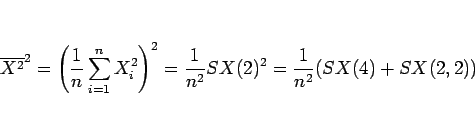$\begin{displaymath} \overline{X^2}^2 = \left(\frac{1}{n}\sum_{i=1}^nX_i^2\right)^2 = \frac{1}{n^2} SX(2)^2 = \frac{1}{n^2} (SX(4)+SX(2,2))\end{displaymath}$ (13)

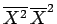となる。次に、 $\overline{X^2}\,\overline{X}^2$ は、

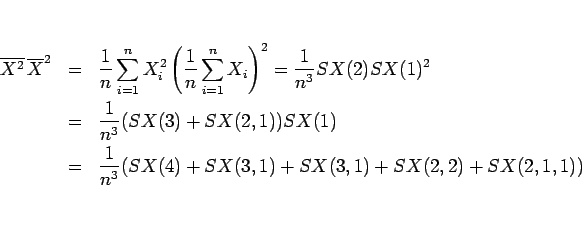
$\begin{eqnarray*}\overline{X^2}\,\overline{X}^2 &=& \frac{1}{n}\sum_{i=1}^nX_i... ...) \\ &=& \frac{1}{n^3}(SX(4)+SX(3,1)+SX(3,1)+SX(2,2)+SX(2,1,1))\end{eqnarray*}$

となるので、

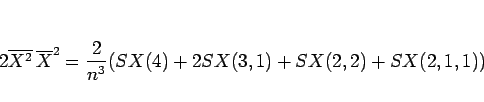$\begin{displaymath} 2\overline{X^2}\,\overline{X}^2 = \frac{2}{n^3}(SX(4)+2SX(3,1)+SX(2,2)+SX(2,1,1))\end{displaymath}$ (14)

となる。最後に、 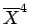$\overline{X}^4$ は、

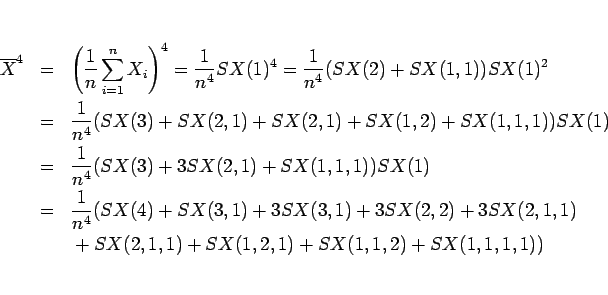
$\begin{eqnarray*}\overline{X}^4 &=& \left(\frac{1}{n}\sum_{i=1}^nX_i\right)^4 ... ...+3SX(2,1,1) \\ && {}+SX(2,1,1)+SX(1,2,1)+SX(1,1,2)+SX(1,1,1,1))\end{eqnarray*}$

となるので、

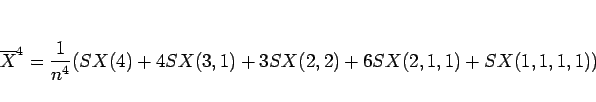$\begin{displaymath} \overline{X}^4 = \frac{1}{n^4}(SX(4)+4SX(3,1)+3SX(2,2)+6SX(2,1,1)+SX(1,1,1,1))\end{displaymath}$ (15)

となる。

(13), (14), (15) より、

$\displaystyle {\overline{X^2}^2-2\overline{X^2}\,\overline{X}^2+\overline{X}^4}$
	$\textstyle =$	$\displaystyle \frac{1}{n^2}(SX(4)+SX(2,2)) -\frac{2}{n^3}(SX(4)+2SX(3,1)+SX(2,2)+SX(2,1,1))$
		$\displaystyle {}+\frac{1}{n^4}(SX(4)+4SX(3,1)+3SX(2,2)+6SX(2,1,1)+SX(1,1,1,1))$
	$\textstyle =$	$\displaystyle \frac{(n-1)^2}{n^4}SX(4) -\frac{4(n-1)}{n^4}SX(3,1) +\frac{n^2-2n+3}{n^4}SX(2,2)$
		$\displaystyle {}-\frac{2(n-3)}{n^4}SX(2,1,1) +\frac{1}{n^4}SX(1,1,1,1)$	(16)

となる。

竹野茂治＠新潟工科大学
2013年7月4日