3 不偏分散、標本分散の平均
本節では、不偏分散、標本分散の平均 (確率変数としての平均) を計算する。
そのために、平方和 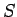 の平均をまず求める。
の平均をまず求める。
(2) により、
![\begin{displaymath}
E[S] = nE[\overline{X^2}-\overline{X}^2]
\end{displaymath}](img41.gif)
となるが、
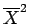 を
を
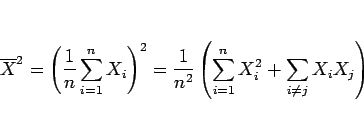
と展開すれば、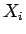 は互いに独立なので
は互いに独立なので 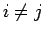 のとき
のとき
![$E[X_iX_j]=E[X_i]E[X_j]$](img45.gif) であり、
よって、今後
であり、
よって、今後
![$E[X_i^k]=\xi_k$](img46.gif) と書くことにすれば、
と書くことにすれば、
![\begin{eqnarray*}E[S]
&=&
n\cdot\frac{1}{n}\sum_{i=1}^nE[X_i^2]
-n\cdot\frac...
..._2 - \frac{1}{n}\cdot \Perm{n}{2}\xi_1^2
=
(n-1)(\xi_2-\xi_1^2)\end{eqnarray*}](img47.gif)
となる。ここで、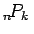 は
は 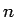 個から
個から 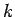 個を取って並べる順列の数で、
個を取って並べる順列の数で、
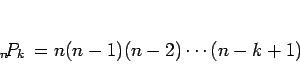
である。一方、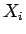 の分散
の分散 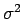 は、
は、
![\begin{displaymath}
\sigma^2
= V[X_i]
= E[(X_i-\mu)^2]
= E[X_i^2]-E[X_i]^2
\end{displaymath}](img50.gif)
より、
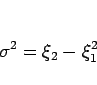 |
(5) |
となるので、結局、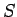 の平均は、
の平均は、
![\begin{displaymath}
E[S] = (n-1)\sigma^2
\end{displaymath}](img52.gif)
であることがわかり、よって不偏分散、標本分散の平均は、
![\begin{displaymath}
E[V_1] = \frac{1}{n-1}E[S] = \sigma^2,
\hspace{1zw}
E[V_1] = \frac{1}{n}E[S] = \frac{n-1}{n}\sigma^2\end{displaymath}](img53.gif) |
(6) |
となる。
竹野茂治@新潟工科大学
2013年7月4日